Глава 7. Введение в проблему статистического вывода

V

Выбор критерия представляет собой отдельную проблему

будет рассматриваться нами в следующей главе. А сейчас будем исходить из того, что исследователь уже решил проблему выбора критерия, и рассмотрим общую последовательность проверки гипотезы.

При обработке данных на компьютере при помощи статистической про­граммы (например, SPSS) исследователю достаточно указать программе, ка­кой критерий (метод, тест) необходимо применить к заданной выборке ис­ходных данных. Далее программа сама вычисляет эмпирическое значение критерия и сопоставляет его с теоретическим распределением. В качестве ре­зультата исследователь получает значение ^-уровня значимости, наряду с эм­пирическим значением критерия и числом степеней свободы.

Когда расчеты производятся «вручную», исследователь совершает более сложную последовательность действий для проверки гипотезы, включающую применение специальных таблиц критических значений критерия:

1. Выбор критерия в зависимости от вида исходных данных и статистичес­ кой гипотезы: теоретического распределения, формул расчета эмпири­ ческого значения критерия и числа степеней свободы.

2. Расчет по исходным данным (или по имеющимся статистикам) эмпи­ рического значения критерия и числа степеней свободы.

3. Применение «Таблицы критических значений критерия» позволяет оп­ ределить значение /?-уровня для данного числа степеней свободы.

Таблица критических значений содержит значения (квантили) теоретичес­кого распределения, соответствующие наиболее важным — критическим зна­чениям /ьуровня (0,1; 0,05; 0,01 и т. д.) для различных чисел степеней свободы. /7-уровепь значимости по вычисленному эмпирическому значению критерия при помощи таких таблиц определяется следующим образом. Для данного числа степеней свободы по таблице определяются ближайшие критические значения и/?-уровни, им соответствующие. Далее значение р-уровня опреде­ляется в виде неравенства по правилу, которое демонстрируется на рис. 7.2 (значимость возрастает слева направо, в соответствии с убыванием /ьуровня):

П если эмпирическое значение критерия (К_э) находится между двумя кри­тическими значениями, то /^-уровень меньше того критического р, ко­торое находится левее;

101

Часть II. Методы статистического вывода: проверка гипотез

П если К^ находится левее крайнего левого критического значения (обычно это соответствует критическому^ = 0,1, реже — р = 0,05), то ^-уровень больше, чем крайнее правое критическое значение р;

О если К_э находится правее крайнего правого критического значения, то /ьуровень меньше крайнего правого критического р.

Например, если эмпирическое значение критерия (К_э) находится между А^₀₅ и А'оо,, то р < 0,05. Если К_э находится левее ЛГ_О>Ь то р > 0,1. Если А^ находится правее Ао_ОП,, тор < 0,001.

Решение исследователя:

р>0,1 р<0,1 р<0,05 р < 0,01 р< 0,001

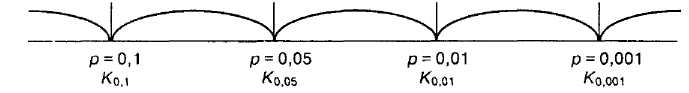
Рис. 7.2. Схема определения/^-уровня (р~ ... — критические значения/ьуровня, К — соответствующие критические значения критерия)

Для разных критериев возможны разные соотношения между р-уровнем и величиной критических его значений. Для большинства критериев (t, F, у} и др.) — чем больше значение критерия, тем выше статистическая значимость (меньше/^-уровень). Но для некоторых критериев зависимость обратная. На­пример, £/-Манна-Уитни или Т-Вилкоксона убывают по мере увеличения уровня значимости (уменьшения ^-уровня). Тем не менее, правило остается общим, в соответствии со схемой на рис. 7.2. Например, если t₃ находится между /₀, и г₀₀₅ (т. е. /₀,i < t₃< t_Q$₅), тор < 0,1. И если 1/_э находится между U_Ql и £/о,о5 (т.^е- ^о,о5 ^< &>< £/o,i)>to/K 0,1. Если же эмпирическое значение попадает левее критического для р = 0,1 (/_э < t_Q>ь но С/_э > U_o^), то уровень значимости определяется как/j > 0,1.

ПРИМЕРЫ

1. Гипотеза Н_о: М -100 проверяется при помощи критерия /-Стьюдента. Для вы­ числения эмпирического значения критерия t₃ применяется формула 7.2. На выборке vV= 36 получены следующие значения статистик: М= 107,5, о = 15. По формуле 7.2 t₃- 3, df= 35. Далее воспользуемся таблицей критических значений /-Стьюдента (приложение 2). В этой таблице строки соответствуют df— числам степеней свободы, столбцы — критическим значениям р-уровня. В строке для df— 35 обнаруживаем, что наше эмпирическое значение попадает в интервал между значениями 2,724 (для р - 0,01) и 3,591 (для р ~ 0,001). Следовательно, вероятность того, что Н_о верна, р < 0,01.

2. Предположим, та же гипотеза проверяется на выборке N — 36, но получены сле­ дующие значения статистик: М= 102,5, а— 15. По формуле 1_Э=\, df= 35. Вос­ пользовавшись той же таблицей критических значений, обнаруживаем, что наше эмпирическое значение меньше, чем /_Oil = 1,69. Следовательно, в соответ­ ствии со схемой на рис. 7.2, р > 0,1.

102