Глава 12. Непараметрические методы сравнения выборок

N< 5, то пользуются дополнительными таблицами критических значений Х²-Фридмана (приложение 13).

При отклонении нулевой статистической гипотезы об отсутствии разли­чий принимается альтернативная гипотеза о статистически достоверных раз­личиях выборок по изучаемому признаку — без конкретизации направления различий. Для утверждений о том, что уровень выраженности признака в ка­кой-то из сравниваемых выборок выше или ниже, необходимо парное соотнесение выборок по критерию Т-Вилкоксона.

ПРИМЕР 12.4

Проверим гипотезу о различии четырех зависимых выборок по уровню выражен­ности признака Х(о различии четырех условий для одной и той же выборки). Для принятия статистического решения а = 0,05:

Ш а г 1. Для каждого объекта условия ранжируются (по строке).

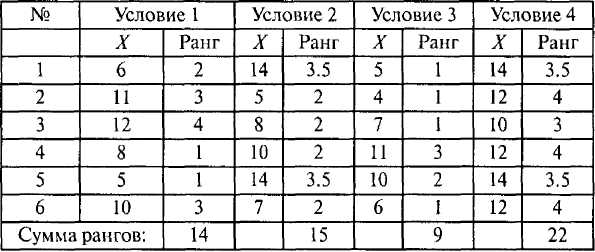
Ш а г 2. Вычисляется сумма рангов для каждого условия: R_: — 14, R₂ = 15, /?₃ ~ 9, /?4=22.

Ш а г 3. Вычисляется эмпирическое значение х²-Фридмана по формуле 12.3:

Ш а г 4. Определяется р-уровень значимости. Так как к > 3, jV> 4, то пользуются обычной таблицей для х² (приложение 4). Эмпирическое значение у² находится меж­ду критическими для р = 0,05 нр = 0,01. Следовательно, р < 0,05.

Ш а г 5. Принимается статистическое решение и формулируется содержательный вывод. На уровне а = 0,05 гипотеза Н_о отклоняется. Содержательный вывод: срав­ниваемые условия статистически достоверно различаются по уровню выраженно­сти признака {р < 0,05).

Отметим, что на основании такой проверки мы не можем сделать конкретный вы­вод о направлении различий и о том, в каких условиях признак принимает боль­шие или меньшие значения. Для этого необходимо парное соотнесение условий по соответствующему критерию (Г-Вилкоксона).

183

Часть II. Методы статистического вывода: проверка гипотез Обработка на компьютере: критерий х2-Фридмана

Для обработки использованы данные примера 12.4. Исходные данные для обработки введены в таблицу (Data Editor) в виде четырех переменных, соот­ветствующих четырем сравниваемым условиям (varl,..., var4).

A) Выбираем Analyze > Nonparametric Tests > К-Related Samples... (для /с-зависимых выборок).

Б) В открывшемся окне диалога выделяем переменные (соответствующие нескольким измерениям одного и того же признака) и переносим их при по­мощи кнопки > из левого окна в правое окно (Test Variables). Переменных должно быть больше двух (в данном случае 4). Нажимаем ОК.

B) Получаем результаты в виде двух таблиц:

Ranks

	Mean	Rank
VAR1	2.	33
VAR2	2.	50
VAR3	1.	50
VAR4	3 .	67
Test Statistics(a)
N		6
Chi-Square		8.897
df		3
Asymp. Sig.		.031

a Friedman Test

В первой таблице содержатся ранговые статистики: средние ранги для каж­дой группы (Mean Rank). Во второй таблице содержатся результаты проверки гипотезы: эмпирическое значение критерия %² (Chi-Square), число степеней свободы (df) и/7-уровень значимости (Asymp. Sig.).