Глава 12. Непараметрические методы сравнения выборок

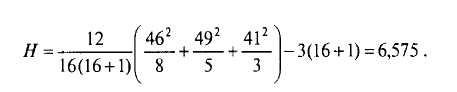
Шаг 5. Определяется /?-уровень значимости. Хотя сравниваются 3 выборки, но объем одной из них больше 5, поэтому вычисленное Я сравнивается с табличным значением х² (приложение 4) для числа степеней свободы df— 3 — 1—2. Эмпириче­ское значение Я находится между критическими для р = 0,05 и р = 0,01. Следова­тельно, р < 0,05.

Ш а г 6. Принимается статистическое решение и формулируется содержательный вывод. На уровне а = 0,05 гипотеза Н_о отклоняется. Содержательный вывод: срав­ниваемые выборки различаются статистически достоверно по уровню выраженно­сти признака (р < 0,05).

Отметим, что на основании такой проверки мы не можем сделать конкретный вы­вод о направлении различий и о том, в какой выборке признак принимает большие или меньшие значения. Для этого необходимо парное соотнесение выборок по со­ответствующему критерию (£/-Манна-Уитни).

Обработка на компьютере: критерий я-Краскала-Уоллеса

Для обработки использованы данные примера 12.3. В таблице исходных данных (Data Editor) для каждого из 16 объектов определены значения двух переменных: varl — значения количественного признака, var2 — группи­рующая переменная, обозначающая принадлежность каждого объекта к од­ной из трех сравниваемых групп.

A) Выбираем Analyze > Nonparametric Tests > K-Independent Samples... (для ^-независимых выборок).

Б) В открывшемся окне диалога выделяем и переносим при помощи кноп­ки > из левого окна интересующие переменные в правое верхнее окно (Test Variable(s)) (в данном случае — varl); группирующую переменную, которая делит выборку на подгруппы (Grouping Variable) (в данном случае — var2). Нажимаем кнопку Define Range... и задаем диапазон градаций группирующей переменной (градации должны нумероваться подряд) — от минимума (Mini­mum) до максимума (Maximum) (в данном случае — от 1 до 3). Нажимаем Continue. Нажимаем ОК.

B) Получаем результаты в виде двух таблиц:

Ranks
	VAR2	N	Mean Rank
VAR1	1.00	8	5.75
	2.00	5	9.80
	3.00	3	13.67
	Total	16

181

Часть II. Методы статистического вывода: проверка гипотез

Test Statistics(a,b)

	VAR1
Chi-Square df Asymp. Sig.	6.575 2 .037

a Kruskal Wallis Test

b Grouping Variable: VAR00006

В первой таблице содержатся ранговые статистики: средние ранги для каж­дой группы (Mean Rank). Во второй таблице содержатся результаты проверки гипотезы: эмпирическое значение критерия %² (Chi-Square), число степеней свободы (df) и ^-уровень значимости (Asymp. Sig.).

Сравнение более двух зависимых выборок

Критерий %²-Фридмана (Friedman test) является непараметрическим анало­гом однофакторного дисперсионного анализа (ANOVA) для повторных изме­рений. Он позволяет проверять гипотезы о различии более двух зависимых выборок (повторных измерений) по уровню выраженности изучаемого при­знака. Критерий х²-Фридмана может быть более эффективен, чем его метри­ческий аналог ANOVA в случаях повторных измерений изучаемого признака на небольших выборках.

Критерий х²-Фридмана основан на ранжировании ряда повторных изме­рений для каждого объекта выборки. Затем вычисляется сумма рангов для каж­дого из условий (повторных измерений). Если выполняется статистическая гипотеза об отсутствии различий между повторными измерениями, то можно ожидать примерное равенство сумм рангов для этих условий. Чем больше раз­личаются зависимые выборки по изучаемому признаку, тем больше эмпири­ческое значение %²-Фридмана.

Эмпирическое значение х²-Фридмана вычисляется после ранжирования ряда повторных измерений для каждого объекта по формуле:

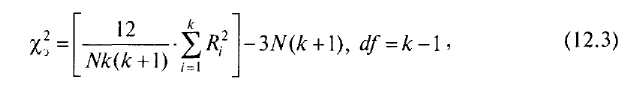
где N — число объектов (испытуемых), к — количество условий (повторных измерений), R_t — сумма рангов для условия /.

При расчетах «вручную» для определения/г-уровня пользуются таблицами критических значений. Если к = 3, N> 9 или к > 3, N> 4, то пользуются обыч­ной таблицей для %², df= к — 1 (приложение 4). Если к = 3, N< 10 или к = 4,

182