Часть II. Методы статистического вывода: проверка гипотез

сначала перейти от г-Спирмена к т-Кендалла (или наоборот), а затем прове­рить другие возможные причины недостоверности связи.

1. Нелинейность связи: просмотреть график двумерного рассеивания. Если связь не монотонная, то делить выборку на части, в которых связь мо­ нотонная, или делить выборку на контрастные группы и далее сравни­ вать их по уровню выраженности признака.

2. Неоднородность выборки: просмотреть график двумерного рассеивания. Попытаться разделить выборку на части, в которых связь может иметь разные направления.

Если связь статистически достоверна, то прежде, чем делать содержатель­ный вывод, следует исключить возможность наличия «ложной» корреляции, как следствия влияния третьей переменной (см. Замечания к применению метрических коэффициентов корреляции).

АНАЛИЗ КОРРЕЛЯЦИОННЫХ МАТРИЦ

Корреляционная матрица. Часто корреляционный анализ включает в себя изучение связей не двух, а множества переменных, измеренных в количествен­ной шкале на одной выборке. В этом случае вычисляются корреляции для каждой пары из этого множества переменных. Вычисления обычно прово­дятся на компьютере, а результатом является корреляционная матрица.

Корреляционная матрица (Correlation Matrix) — это результат вычисления корреляций одного типа для каждой пары из множества Р переменных, изме­ренных в количественной шкале на одной выборке.

ПРИМЕР

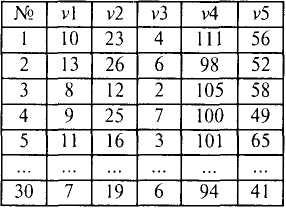
Предположим, изучаются связи между 5 переменными (vl, v2,..., v5; P= 5), изме­ренными на выборке численностью N=30 человек. Ниже приведена таблица ис­ходных данных и корреляционная матрица.

Исходные данные:

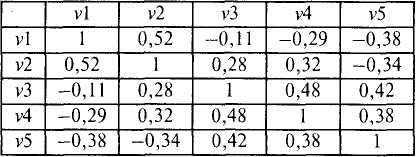
Корреляционная матрица:

Нетрудно заметить, что корреляционная матрица является квадратной, симметрич­ной относительно главной диагонали (таккакг,у= /}_у), с единицами на главной диа­гонали (так как г_и = Гу = 1).

156

Глава 10. Корреляционный анализ

Корреляционная матрица является квадратной: число строк и столбцов равно числу переменных. Она симметрична относительно главной диагона­ли, так как корреляция х с у равна корреляции у с х. На ее главной диагонали располагаются единицы, так как корреляция признака с самим собой равна единице. Следовательно, анализу подлежат не все элементы корреляцион­ной матрицы, а те, которые находятся выше или ниже главной диагонали.

Количество коэффициентов корреляции, подлежащих анализу при изучении связей Рпризнаков определяется формулой: Р(Р- 1)/2. В приведенном выше примере количество таких коэффициентов корреляции 5(5 — 1)/2 = 10.

Основная задача анализа корреляционной матрицы — выявление структуры взаимосвязей множества признаков. При этом возможен визуальный анализ корреляционных плеяд — графического изображения структуры статистически значимых связей, если таких связей не очень много (до 10—15). Другой спо­соб — применение многомерных методов: множественного регрессионного, факторного или кластерного анализа (см. раздел «Многомерные методы...»). Применяя факторный или кластерный анализ, можно выделить группиров­ки переменных, которые теснее связаны друг с другом, чем с другими пере­менными. Весьма эффективно и сочетание этих методов, например, если признаков много и они не однородны.

Сравнение корреляций — дополнительная задача анализа корреляционной матрицы, имеющая два варианта. Если необходимо сравнение корреляций в одной из строк корреляционной матрицы (для одной из переменных), при­меняется метод сравнения для зависимых выборок (с. 148—149). При сравне­нии одноименных корреляций, вычисленных для разных выборок, применя­ется метод сравнения для независимых выборок (с. 147-148).

Методы сравнения корреляций в диагоналях корреляционной матрицы (для оценки стационарности случайного процесса) и сравнения нескольких корре­ляционных матриц, полученных для разных выборок (на предмет их одно­родности), являются трудоемкими и выходят за рамки данной книги. Позна­комиться с этими методами можно по книге Г. В. Суходольского¹.

Проблема статистической значимости корреляций. Проблема заключается в том, что процедура статистической проверки гипотезы предполагает одно­кратное испытание, проведенное на одной выборке. Если один и тот же метод применяется многократно, пусть даже и в отношении различных переменных, то увеличивается вероятность получить результат чисто слу­чайно. В общем случае, если мы повторяем один и тот же метод проверки гипотезы к раз в отношении разных переменных или выборок, то при уста­новленной величине а мы гарантированно получим подтверждение гипоте­зы в ахк числе случаев.

Предположим, анализируется корреляционная матрица для 15 переменных, то есть вычислено 15(15—1)/2 = 105 коэффициентов корреляции. Для проверки гипотез установлен уровень а = 0, 05. Проверяя гипотезу 105 раз, мы пять раз (!) получим ее подтверждение независимо от того, существует ли связь на самом деле. Зная это и

Суходольский Г. В. Основы математической статистики для психологов. СПб., 1998. С. 299-302.

157