Глава 10. Корреляционный анализ

Для статистической проверки подобных гипотез применяется Z-критерий, эмпирическое значение которого вычисляется по формуле:

. - rlУ + (1 - гД )² - 2^ - (2^ - /у_хг)(1 - г²_ху - ^ - 4>

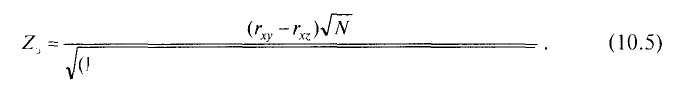
ПРИМЕР 10.3 (продолжение)

П роверим гипотезу о различии коэффициентов корреляции (а = 0,05).

Ш а г 1. Вычислим эмпирическое значение Z-критерия по формуле 10.5: Z, = 2,l 19.

Ш а г 2. Определим /^-уровень значимости. По таблице стандартных нормальных вероятностей (приложение 1) определяем площадь справа от табличного z, ближай­шего меньшегоZ,. Справаотг= 2,11: /*= 0,0174. Уровень значимости определяется по формуле р<2Р. Следовательно, р < 0,035.

Ш а г 3. Принимаем статистическое решение и формулируем содержательный вы­вод. Статистическое решение: отклоняем Н_о (о равенстве корреляций в генераль­ной совокупности). Содержательный вывод: корреляция второй шкалы теста стати­стически достоверно ниже корреляции первой шкалы со средним баллом отметок студентов 2-го курса (р < 0,05) — прогностическая ценность первой шкалы выше, чем второй шкалы.

Отметим, что для решения такой задачи можно было бы рассматривать вы­борки как независимые и применять соответствующий метод сравнения кор­реляций — по формулам 10.3 и 10.4. Но чувствительность (мощность) такой проверки была бы гораздо ниже. В частности, применяя кданным примера 10.3 предыдущий метод, мы получим/? = 0,18, что приводит к принятию Н_о.

КОРРЕЛЯЦИЯ РАНГОВЫХ ПЕРЕМЕННЫХ

Если к количественным данным неприменим коэффициент корреляции г-Пирсона, то для проверки гипотезы о связи двух переменных после предвари­тельного ранжирования могут быть применены корреляции r-Спирмеиа или т-Кендалла.

r-Спирмена. Этот коэффициент корреляции вычисляется либо путем при­менения формулы /"-Пирсона к предварительно ранжированным двум пе­ременным, либо, при отсутствии повторяющихся рангов, по упрощенной формуле:

7V(7V² -1)

153

Часть II. Методы статистического вывода: проверка гипотез

Поскольку этот коэффициент — аналог /--Пирсона, то и применение /•-Спирмена для проверки гипотез аналогично применению /--Пирсона, изло­женному ранее¹.

Преимущество r-Спирмена по сравнению с /--Пирсона — в большей чув­ствительности к связи в случае:

• существенного отклонения распределения хотя бы одной переменной от нормального вида (асимметрия, выбросы);

• криволинейной (монотонной) связи.

Недостаток r-Спирмена по сравнению с /--Пирсона — в меньшей чувстви­тельности к связи в случае несущественного отклонения распределения обе­их переменных от нормального вида.

Частная корреляция и сравнение корреляций применимы и к г-Спирмена.

т-Кендалла. Применяется к предварительно ранжированным данным как альтернатива /--Спирмена. т-Кендалла, как отмечалось в главе 6, имеет более выгодную, вероятностную интерпретацию. Общая формула для вычисления r-Кендалла, вне зависимости от наличия или отсутствия повторяющихся ран­гов (связей):

P^Q

J[N(N-\)/2]-Kj[N(N-\)/2]-K_y '

где Р — число совпадений, Q — число инверсий, К_х и К_у — поправки на связи в рангах (см. главу 6: Проблема связанных (одинаковых) рангов). Если связей в рангах нет, то знаменатель формулы равен Р+ Q= N(N~\)/2.

Поскольку природа г-Кендалла иная, чем у r-Спирмена и /--Пирсона, то /^-уровень определяется по-другому: применяется г-критерий и единичное нормальное распределение. Эмпирическое значение вычисляется по формуле:

где Р — число совпадений, Q — число инверсий, К_х и К_у — поправки на связи в рангах (см. главу 6: Проблема связанных (одинаковых) рангов). Если связей в рангах нет, то знаменатель формулы равен Р+ Q= N(N~\)/2.

(.0.6,

Поскольку природа г-Кендалла иная, чем у г-Спирмена и /--Пирсона, то /^-уровень определяется по-другому: применяется г-критерий и единичное нормальное распределение. Эмпирическое значение вычисляется по формуле:

При вычислениях «вручную» /^-уровень определяется по следующему ал­горитму:

а) вычисляется эмпирическое значение г_э;

б) по таблице «Стандартные нормальные вероятности» (приложение 1) определяется теоретическое значение х, ближайшее меньшее к эмпири­ ческому значению z₃',

в) определяется площадь Рпод, кривой справа от г_т;

г) вычисляется ^-уровень по формуле/? < 2Р.

Проверяемая статистическая гипотеза, порядок принятия статистическо­го решения и формулировка содержательного вывода те же, что и для случая г-Пирсона или г-Спирмена.

¹ В некоторых источниках по непонятным причинам для /--Пирсона и r-Спирмена приво­дят разные таблицы критических значений. В компьютерных программах (SPSS, STATISTICA) уровни значимости для одинаковых /--Пирсона и r-Спирмена всегда совпадают.

154

При вычислениях на компьютере статистическая программа (SPSS, Statistica) сопровождает вычисленный коэффициент корреляции более точным значени­ем /ьуровня.

ПРИМЕР 10.4

Предположим, для каждого из 12 учащихся одного класса известно время решения тестовой арифметической задачи в секундах (X) и средний балл отметок по мате­матике за последнюю четверть (Y). При подсчете т-Кендалла были получены сле­дующие результаты: Р= 18; Q= 48; т = —0,455. Проверим гипотезу о связи времени решения тестовой задачи и среднего балла отметок по математике.

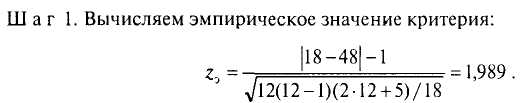
Ш а г 2. По таблице «Стандартные нормальные вероятности» (приложение 1) на­ходим ближайшее меньшее, чем z₃, теоретическое значение z_T и площадь справа от этого z,: z_T - 1,98; площадь справа Р = 0,024.

Ш а г 3. Вычисляемр-уровень по формуле/) < 2Р;р < 0,048.

Ш а г 4. Принимаем статистическое решение. Нулевая гипотеза об отсутствии свя­зи в генеральной совокупности отклоняется на уровне а = 0,05.

Ш а г 5. Формулируем содержательный вывод. Обнаружена отрицательная связь между временем решения тестовой арифметической задачи и средним баллом отме­ток по математике за последнюю четверть (х = -0,455; N= \2;p< 0,048). Величина корреляции показывает, что при сравнении испытуемых друг с другом более высокий средний балл будет сочетаться с меньшим временем решения за­дач чаще, чем в 70% случаях, так как вероятность инверсий P{q) = (1 — т)/2 = = (1+0,455)/2 = 0,728.

(Отметим, что при вычислении т-Кендалла по этим данным на компьютере были получены следующие результаты: т = -0,455; р = 0,040.)

Сравнениеr-Спирменаих-Кендалла. Интерпретация r-Спирмена аналогична интерпретации r-Пирсона. Квадрат и того, и другого коэффициента корреля­ции (коэффициент детерминации) показывает долю дисперсии одной пере­менной, которая может быть объяснена влиянием другой переменной. х-Кен-далла имеет другую интерпретацию: это разность вероятностей совпадений и инверсий в рангах. Кроме того, по величине х-Кендалла можно судить о веро­ятности совпадений Р{р) = (1 + т)/2 или инверсий P{q) = (1 — х)/2.

Для одних и тех оке данных величина r-Спирмена всегда больше, чем х-Кендал­ла, исключая крайние значения 0 и 1. Это отражает тот факт, что х-Кендалла зависит от силы связи линейно, а r-Спирмена — не линейно. В то же время для одних и тех же данных р-уровень i-Кендалла и r-Спирмена примерно одина­ков, а иногда х-Кендалла имеет преимущество в уровне значимости.

Замечания к применению. Если связь (статистически достоверная) не обна­ружена, но есть основания полагать, что связь на самом деле есть, то следует

155