Глава 7. Введение в проблему статистического вывода

ности (в данном случае — А — 10), а дисперсия выборочных средних составит величину т² = o^/N, где о_х² — дисперсия совокупности, N — объем каждой выборки (т еще называют ошибкой среднего).

Таким образом, заранее известно распределение средних для случая, когда верна Н_о. Это распределение позволяет определить, насколько вероятно то или иное случайное отклонение выборочного среднего от А — среднего в ге­неральной совокупности. Например, из свойств нормального распределения мы знаем, что примерно 68% площади под кривой нормального распределе­ния находится в диапазоне ± о от среднего значения. Следовательно, 68% всех выборочных средних будет находиться в диапазоне А±т. Вероятность того, что выборочное среднее случайно попадет в этот диапазон составляет 0,68, а вероятность того, что оно будет отличаться от А больше чем на \т составляет 1 — 0,68 = 0,32. Аналогичным образом мы можем определить, насколько веро­ятно получение данного конкретного (или большего) отклонения выбороч­ного среднего от А при условии истинности Н_о.

Для нашего примера необходимо сначала определить, насколько выбороч­ное среднее отличается от А в единицах стандартного отклонения, то есть оп­ределить соответствующее г-значение:

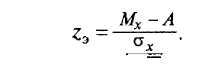
In

Формулы, подобные 7.1, позволяют получить так называемое эмпиричес­кое значение критерия для соответствующего теоретического распределения (в данном случае формула 7.1 позволяет вычислить эмпирическое значение z-критерия — для нормального распределения). Подставляя выборочные зна­чения, получаем z — 2. По таблице параметров нормального распределения можно определить, что в диапазоне ±2 находится 0,954 всей площади под кри­вой. В соответствии с интерпретацией единичной нормальной кривой, этой площади соответствует вероятность того, что случайное отклонение от 0 бу­дет меньше z⁼ ±2. А для нашего случая найденная площадь соответствует ве­роятности того, что случайное отклонение выборочного среднего значения будет меньше +(М_К — А) — ±0,6. Соответственно, вероятность случайного от­клонения выборочного среднего от генерального среднего на 0,6 и больше определяется площадью в «хвостах» под кривой нормального распределения — за пределами найденного диапазона (рис. 7.1). Следовательно, вероятность того, что данная выборка принадлежит генеральной совокупности со сред­ним А (то есть, что верна Н_о), составляет/? = 1 — 0,954 = 0,046. Это и есть веро­ятность того, что данный выборочный результат мог быть получен случайно, когда на самом деле в генеральной совокупности верна Н_о или то, что называется р-уровнем значимости.

Следует отметить, что выборочное распределение средних значений соот­ветствует нормальному виду, если N > 100. Для выборок меньшего объема рас­пределение средних начинает зависеть от объема выборок (точнее — от числа степеней свободы, df) и соответствует другому теоретическому распределе-

97

Часть II. Методы статистического вывода: проверка гипотез

I

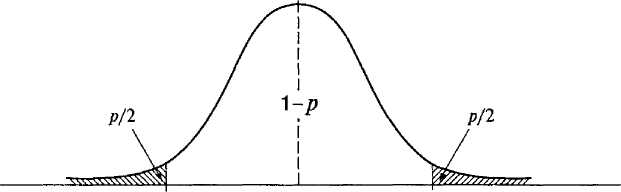
Рис. 7.1. Выборочное распределение средних значений для верной Н_о

нию — /-Стыодента. Тем не менее, общая последовательность проверки ста­тистической гипотезы остается той же, как, впрочем, и для любого другого случая. Сначала вычисляется соответствующее эмпирическое значение:

I W _.. А I

df=N-l. (7.2)

Затем вычисленное эмпирическое значение сопоставляется с теоретичес­ким /-распределением для соответствующего числа степеней свободы df. Это позволяет определить /^-уровень — вероятность того, что выборка принадле­жит генеральной совокупности, для которой верна нулевая гипотеза Н_о: М — А.

Таким образом, в основе статистической проверки гипотез лежит представ­ление о теоретическом распределении выборочной статистики — для условия, когда в генеральной совокупности верна нулевая статистическая гипотеза. В исследовании Арбутнота в качестве теоретического выступало биномиаль­ное распределение для Н_о: Р — '/₂, а в нашем примере — распределение выбо­рочных средних для известной нулевой гипотезы (Z-распределение для боль­ших N и /-распределение для малых N). В процессе проверки статистической гипотезы определяется /^-уровень значимости (вероятность того, что нулевая статистическая гипотеза верна) путем соотнесения эмпирических значений выборочных статистик (например, разности средних) с теоретическим рас­пределением, соответствующим нулевой статистической гипотезе.

УРОВЕНЬ СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ

Статистическая значимость (Significant level, сокращенно Sig.), или р-уро-вень значимости (р-level), — основной результат проверки статистической ги­потезы. Говоря техническим языком, это вероятность получения данного ре­зультата выборочного исследования при условии, что на самом деле для генеральной совокупности верна нулевая статистическая гипотеза — то есть связи нет. Иначе говоря, это вероятность того, что обнаруженная связь носит случайный характер, а не является свойством совокупности. Именно статис-

98