Глава 10. Корреляционный анализ

ПРОВЕРКА ГИПОТЕЗ О РАЗЛИЧИИ КОРРЕЛЯЦИЙ

Задача сравнения корреляций имеет два варианта решения: а) для незави­симых выборок — когда необходимо сравнить два коэффициента корреляции, полученных на разных выборках между одними и теми же переменными; б) для зависимых выборок — когда необходимо сравнить корреляцию переменных X и Ус корреляцией переменных Хп Z, при условии, что все три переменные измерены на одной и той же выборке¹.

Сравнение корреляций для независимых выборок

По результатам сравнения корреляций в данном случае можно делать вы­вод о различии корреляции признаков Хч Уъ двух сравниваемых совокупно­стях. Проверяемая Н_о содержит утверждение о равенстве корреляций в гене­ральной совокупности.

ПРИМЕР 10.2

В одном исследовании сравнивалась связь интеллекта и среднего балла отметок учащихся 6-х классов и учащихся 11-х классов. Для 50 учащихся 6-х классов корре­ляция составила г_{ = 0,63 (р < 0,001), а для 60 учащихся 11-х классов — г₂ — 0,31 (р < 0,05). Можно ли на основании этих данных утверждать, что в 11-х классах связь отметок с интеллектом слабее, чем в 6-х классах?

Задача статистической проверки подобных предположений решается при помощи Z-преобразования Фишера коэффициентов корреляции и последу­ющего применения Z-критерия. Z-преобразование Фишера — это пересчет коэффициентов корреляции г по формуле:

_Z = W~- (Ю.З)

2 \-г

Для облегчения пересчета можно воспользоваться функцией «ФИШЕР» в

программе Excel либо таблицей, составленной с ее помощью (приложение 7).

Эмпирическое значение Z-критерия для определения /?-уровня значимое-

Для облегчения пересчета можно воспользоваться функцией «ФИШЕР» в программе Excel либо таблицей, составленной с ее помощью (приложение 7).

Эмпирическое значение Z-критерия для определения /?-уровня значимос­ти различия корреляций вычисляется по формуле:

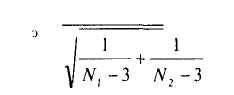
Z = , ^Z'"^Z;_, (10.4)

¹ Методы этого раздела заимствованы из: Гласе Дж., Стенли Дж. Статистические методы is педагогике и психологии. М., 1977. С. 283—286.

151

Часть II. Методы статистического вывода: проверка гипотез

где Z_x и Z₂ — Z-преобразованные значения сравниваемых корреляций, N_x и N₂ — соответствующие объемы выборок. Уровень значимости определяется по формуле р < 2Р, где Р — площадь справа от Z, под кривой нормального распределения.

ПРИМЕР 10.2 (продолжение)

П роверим гипотезу о различии коэффициентов корреляции (а = 0,05).

Ш а г 1. Производим Z-преобразование Фишера в отношении сравниваемых кор­реляций, воспользовавшись таблицей из приложения 7:

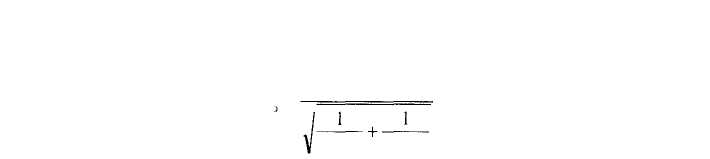
Z, = 0,741; Z₂ = 0,321. Ш а г 2. Вычислим эмпирическое значение Z-критерия по формуле 10.4:

Z = ,⁰'⁷⁴'-°'³²¹ =2,136-

50-3 60-3

Шаг 3. Определим ^-уровень значимости. По таблице стандартных нормальных вероятностей (приложение 1) определяем площадь справа от табличного z, ближай­шего меньшего Z_r Справа от<:= 2,13: Р= 0,0166. Уровень значимости определяется по формуле р<2Р. Следовательно, р < 0,033.

Ш а г 4. Принимаем статистическое решение и формулируем содержательный вы­вод. Статистическое решение: отклоняем Н_о (о равенстве корреляций в генераль­ной совокупности). Содержательный вывод: в 11-х классах связь отметок с интел­лектом статистически значимо ниже, чем в 6-х классах (р < 0,033).

Отметим, что одна и та же разность между корреляциями будет иметь бо­лее высокую статистическую значимость при больших значениях корреляции и меньшую — при более слабых корреляциях. Так, уменьшение значений кор­реляций всего на 0,1 в примере 10.2 привело бы кр > 0,05.

Сравнение корреляций для зависимых выборок

В данном случае предполагается сравнение корреляции Хи Yc корреляци­ей Л¹ и Znpn условии, что все три признака измерены на одной и той же вы­борке. Проверяемая Н_о содержит утверждение о равенстве соответствующих корреляций.

ПРИМЕР 10.3

Сравнивалась прогностическая эффективность двух шкал вступительного теста в отношении предсказания среднего балла отметок студентов 2 курса. На выборке в 95 студентов корреляция результатов тестирования и среднего балла отметок со­ставила: для первой шкалы: /-, = 0,60; для второй шкалы: г₂ = 0,46; корреляция ре­зультатов двух тестов: г_п = 0,70. Можно ли утверждать, что прогностическая цен-

ность первой шкалы достоверно выше, чем второй?

152