Глава 9. Анализ номинативных данных

Проблема направленности гипотезы Н_о должна решаться еще до проведе­ния исследования. Понятно, что исследователя может интересовать любое отклонение от Н_о — как в сторону слишком малого, так и слишком большого числа серий W, Тогда необходима проверка ненаправленной гипотезы. Если же исследователя интересуют только малые значения Жили только слишком большие значения W, то необходима проверка направленной гипотезы. Важ­ность предварительного определения направленности гипотезы обусловлена тем, что при одном и том же числе серий Wр-уровень для направленной гипотезы будет в два раза меньше, чем для ненаправленной гипотезы. Любые сомнения в направленности гипотезы необходимо решать в пользу выбора ненаправлен­ной альтернативы.

Предположим, что для исследователя, получившего данные из примера 9.7, зара­нее не было известно, какая альтернатива будет приниматься в случае отклонения Н_о. Следовательно, должна проверяться ненаправленная Н_о, допускающая откло­нение Н_о как в случае слишком малого, так и в случае слишком большого числа серий W.

Точное распределение числа серий Жпри выполнении Н_о, следовательно, и точное значение р-уровня значимости для конкретного ^(при конкретных значениях тип) может быть получено с помощью комбинаторного анализа, например, при помощи компьютера.

При вычислениях на компьютере точное значение /j-уровня может быть вычислено при выборе опции Exact... (Точно...) в диалоге анализа Runs... (Серии...) с последу­ющим заданием метода Monte Carlo. Так, для примера 9.7 точные значения^-уров-ня (для ненаправленных Н_о, двусторонние): для игрока № 1 р = 0,035; для игрока

Если численность т{п) < 20, то для проверки Н_о применяются таблицы кри­тических значений для числа серий (приложение 5).

ПРИМЕР 9.7 (продолжение)

Проверим ненаправленную Н_о в отношении двух игроков с использованием таб­лицы критических значений числа серий для а = 0,05 (приложение 5). Для этого достаточно соотнести эмпирическое значение числа серий с табличными значе­ниями (нижним Жо 025^и верхним \¥₀ 0975). Если эмпирическое значение меньше или равно 1^0025 ^или больше или равно \¥_0(>975, ^T0 Но отклоняется.

Шаг 1. Принимаем статистические решения. Для т= 10, п= 10: И^з^б; Н^ ₀₉₇5 — 16. Для игрока №1: (С_э = 6, Н_о отклоняется. Для игрока № 2: W₃ - 16, Н_о отклоняется.

Шаг 2. Формулируем содержательные выводы. Для игрока № 1: достоверно чаще после успеха следует успех, а после проигрыша — проигрыш (р< 0,05). Для игрока № 2: по­сле проигрыша достоверно чаще следует выигрыш, а после выигрыша — проигрыш.

Альтернативным способом определения р-уровня является применение Z-критерия серий, основанного на том факте, что число серий Wпри выпол-

143

ЧАСТЬ П. МЕТОДЫ СТАТИСТИЧЕСКОГО ВЫВОДА: ПРОВЕРКА ГИПОТЕЗ

нении Н_о распределено приблизительно нормально с известными M_w и a_w. Формула для определения эмпирического значения Z-критерия серий¹:

Ограничение на применение Z-критерия серий: т > 20, п > 20; т и п несуще­ственно различаются. Если тип существенно различаются, то следует восполь­зоваться комбинаторным методом (например, Монте Карло в программе SPSS).

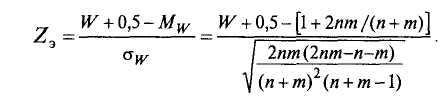
ПРИМЕР9.8

Предположим, исследуется динамика научения в игровом задании. Исследователь предполагает частые повторы проигрышей в начале и выигрышей — в конце пос­ледовательности игр (предполагается проверка направленной гипотезы). Игроком сыграно 40 партий, из них проиграно 20, выиграно 20, число серий 15. К концу последовательности игр наблюдается преобладание выигрышей. Проверим гипо­тезу с применением Z-критерия серий.

Шаг 1. Формулируем Н_о: число серий соответствует случайному распределению выигрышей в последовательности проигрышей (альтернативная Н,: число серий достаточно мало, чтобы говорить о неслучайном преобладании выигрышей в конце последовательности игр). Принимаем а = 0,05.

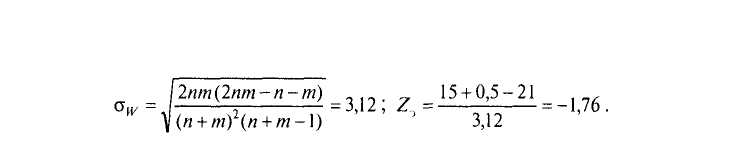
Ш а г 2. Вычислим эмпирическое значение Z-критерия для т = 20; п = 20; И^ =15:

M_w= \ + 2nm/(n+m)=2\;

Ш а г З. Определим/ьуровень. Для этого воспользуемся таблицей стандартных нор­мальных вероятностей (приложение 1). При использовании Z-распределения для проверки направленной гипотезыр-уровень равен площади Рпод нормальной кри­вой справа от +Z, (слева от -Z,). Z, = 1,76 соответствует площадь Р= 0,039. Следо­вательно, р < 0,04.

Ш а г 4. Принимаем статистическое решение и формулируем содержательный вы­вод. Отклоняем Н_о: число серий статистически значимо мало. Содержательный вы­вод: к концу последовательности игр статистически достоверно возрастает частота выигрышей (р < 0,04).

Отметим, что если бы проверялась ненаправленная гипотеза, то найденное значе­ние вероятности Р = 0,039 следовало бы умножить на 2: р < 2Р. Следовательно, р < 0,078, и Н_о на уровне а = 0,05 не отклоняется.

Критерий серий применим для решения двух классов задач. Помимо ис­следования временной последовательности событий Хи Y, или динамики из­менения количественного признака, метод может применяться и для провер-

¹ По Ллойду Э., Ледерману У, с. 131. 144