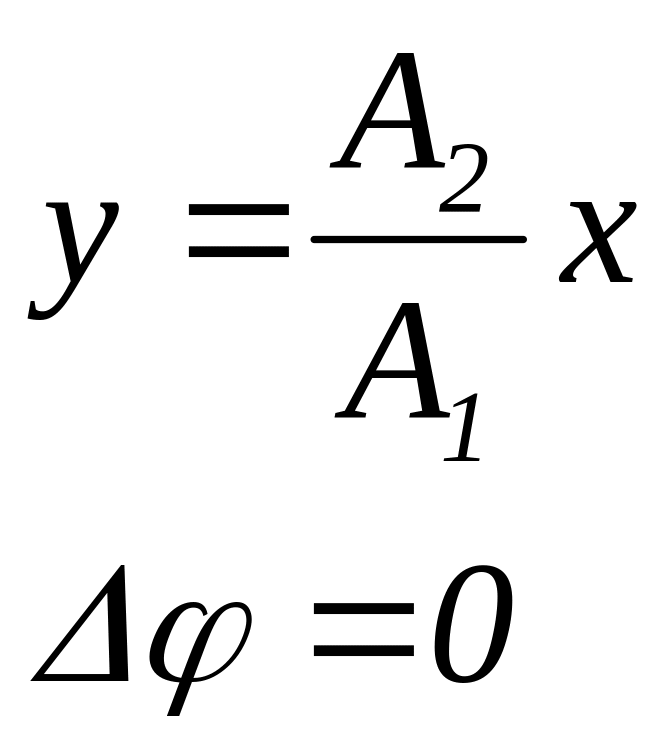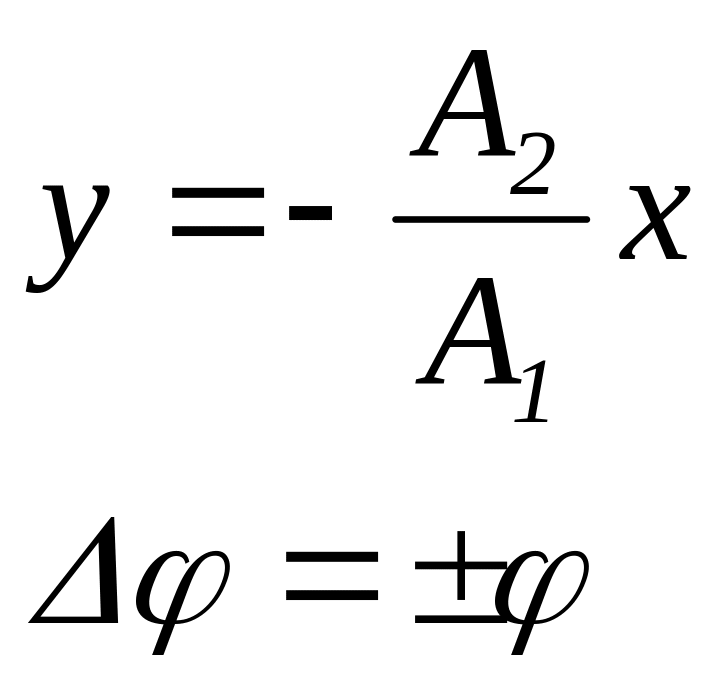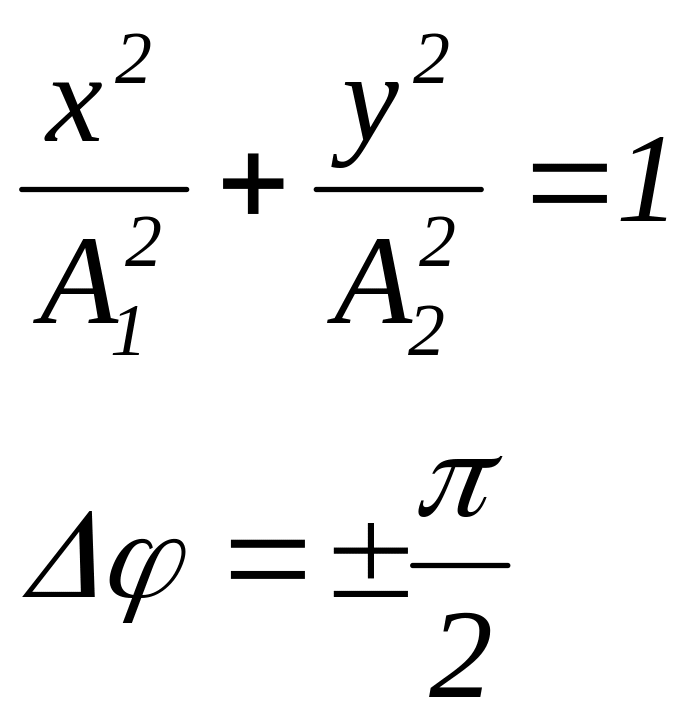Лекция 1. Колебания.
1. Кинематика гармонических колебаний.
Механические колебания - движения тел, повторяющиеся точно или приблизительно через одинаковые промежутки времени.
Условие возникновение колебаний - существование силы, возвращающей тело в положение равновесия при выведении системы из положение равновесия.
Смещением называют проекцию перемещения колеблющегося тела от его положения равновесия на выбранную ось.
Максимальное отклонение тела от положения равновесия называется амплитудой колебаний A.
Промежуток времени, через который колебательная система совершает одно полное колебание называется периодом колебаний T.
Число колебаний совершаемых телом за единицу времени называют частотой колебаний .
Гармоническим колебанием называют ограниченное периодическое движение, при котором смещение относительно положения равновесия происходят по закону синуса или косинуса
х = A sin ( t + 0)
x - смещение, A = Xm - амплитуда колебаний, ( t + 0) - фаза колебаний (величина, стоящая под знаком синуса или косинуса), 0 - начальная фаза колебаний (фаза колебаний в начальный момент времени t=0), = 2 = 2/T – циклическая или круговая частота.
Скорость и амплитуда скорости колеблющегося тела определяется формулами
![]() ;
;
![]() .
.
Ускорение и амплитуда ускорения колеблющегося тела определяется формулами
![]() ;
;
![]() .
.
2. Сложение гармонических колебаний
|
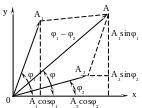
а) Сложение гармонических колебаний одного направления и одинаковой частоты: х1 = A1 cos t х2 = A2 cos( t + ) амплитуда результирующего колебания:
начальная фаза результирующего колебания
|
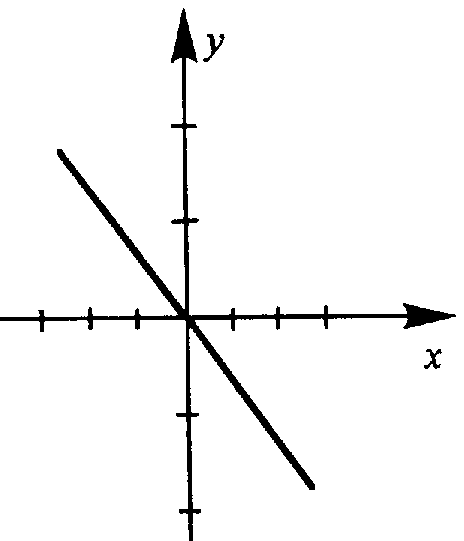
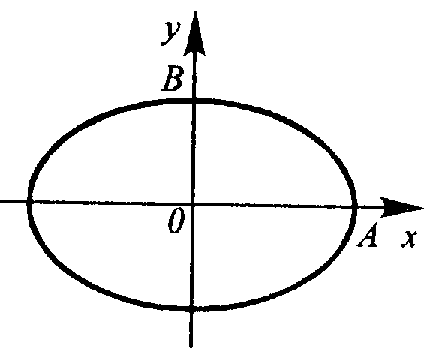
б) Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях
х = A1 cos t y = A2 cos( t + )
а)
|
|
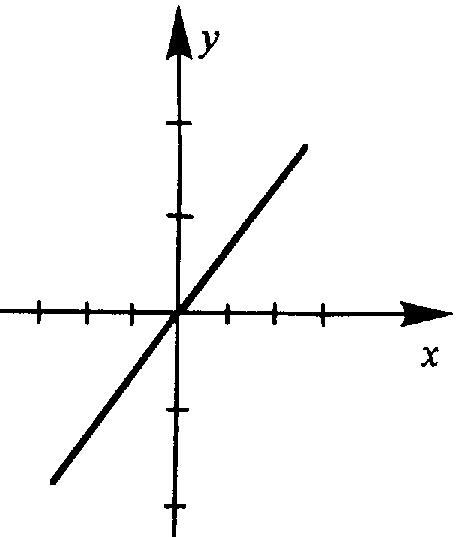
б)
|
|
в)
|
|
2. Маятники. Собственная частота и период колебаний. Энергия гармонических колебаний.
Маятник - твердое тело, совершающее под действием приложенных к нему сил колебания около неподвижной точки или оси.
Материальная точка, подвешенная к неподвижной точке на невесомой нерастяжимой нити, называется математический маятник. Период и циклическая частота колебаний математического маятника определяется по формулам
![]() ;
;
![]() ,
,
где l – длина математического маятника, g – ускорение свободного падения.
Тело, совершающее прямолинейные колебания вдоль заданной оси называется пружинный маятник. Период и циклическая частота колебаний пружинного маятника определяется по формулам
![]() ;
;
![]() ,
,
где k – коэффициент упругости, m – масса тела.
В процессе колебаний происходит перераспределение энергии из кинетической в потенциальную и обратно. При максимальном отклонении тала от положения равновесия тело имеет максимальную потенциальную энергию и минимальную (нулевую) скорость, при прохождении тела через положение равновесия тело имеет максимальную скорость и минимальную (нулевую) потенциальную энергию.
Кинетическая энергия гармонических колебаний определяется формулой
![]()
Максимальная кинетическая энергия гармонических колебаний
![]()
Полная энергия гармонических колебаний согласно закону сохранения энергии равна сумме кинетической и потенциальной энергии:
![]() .
.
Потенциальная энергия гармонических колебаний
![]()
3. Физический маятник.
Абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной неподвижной оси, не проходящей через его центр масс, называется физический маятник.
В случае малых колебаний, период колебаний физического маятника равен
![]()
где J – момент инерции тела относительно оси вращения, m – масса физического маятника, d – расстояние от оси вращения до центра масс физического маятника, g – ускорение свободного падения.
Приведенной длиной физического маятника называется длина математического маятника имеющего такой же период колебаний
![]()
Кинетическая энергия физического маятника
![]()
где φ – угол отклонения от положения равновесия.
Потенциальная энергия физического маятника
![]()