9.1.3. Ефект Зеебека

В

Рис. 9.3.Схема для пояснення ефекту Зеебека:

1-джерело тепла при температурі Т₂, 2-спай провідників А і В; 3-поглинач тепла при температурі Т₁; стрілкою показано напрямок е.р.с.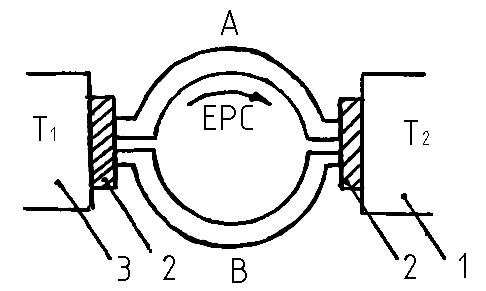

1822р. Зеебек описав явище виникнення термоелектричних струмів в замкнутому колі, складеному із різнорідних провідників, коли контакти (спаї) знаходились при різних температурах.

На рис. 9.З приведено схему, яка складається із двох спаяних провідників А і В (матеріали провідників різні), контакти термостатовані при температурах Т₁ і Т₂ (Т₂ > T₁).

В замкнутому колі виникав струм внаслідок дії термо-е.р.с., величина якої описується рівнянням:

dE_AB = α_ABdT (9.4)

де α_AB – відносний коефіцієнт Зеебека для матеріалів А і В.

Напрямок струму змінюється на зворотній, якщо співвідношення температур спаїв змінити на протилежний.

Використаємо перший закон термодинаміки до переносу по замкнутому колу одиничного заряду і, використавши співвідношення (9.1) та (9.3), знайдемо вираз для повної е.р.с.:

E_AB = π_АВ (Т₂) - π_АВ (Т₁) + 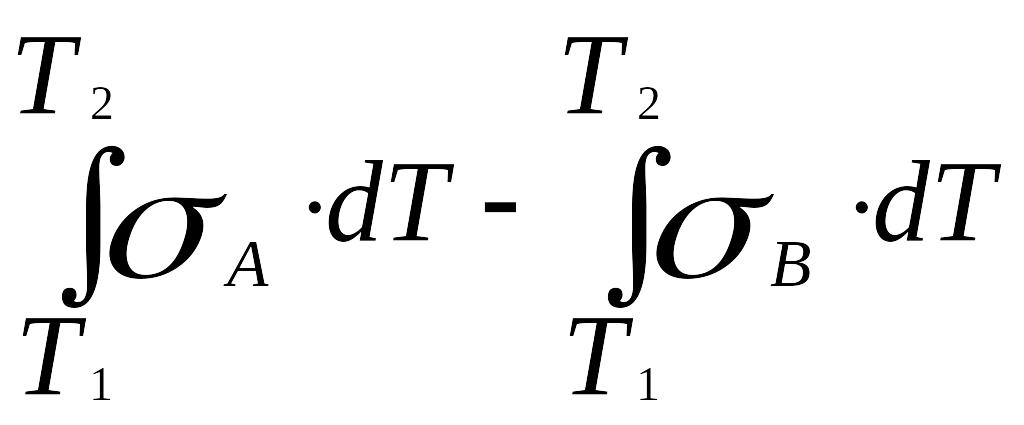(9.5)

Ця величина називається електрорушійною силою Зеебека або термоелектрорушійною силою матеріалу А відносно В в інтервалі температур Т₁ – Т₂.

Якщо прийняти Т₂ = Т₁ + _ΔТ ( _ΔТ << T₁), то можна переписати вираз (9.5) в диференціальній формі:

+ (σ_A - σ_B) = α_AB (9.6)

або dE_AB = α_AB ∙ dT (9.7)

Швидкість зміни Е_AB з температурою (dE_AB/dT) називають температурним коефіцієнтом термо-е.р.с. матеріалу А відносно В або коефіцієнтом Зеебека α_AB.

Співвідношення між коефіцієнтами Пельтьє, Томсона і Зеебека можна одержати за допомогою другого закону термодинаміки шляхом прирівнювання до нуля повної зміни ентропії при переносі по замкнутому колу одиничного заряду:

(9.8)

Підставивши взятий звідси вираз для σ_A - σ_B у рівняння (9.6) знайдемо:

(9.9)

Підставивши вираз (9.9) у (9.8), одержимо:

(9.10)

Рівняння (9.9) і (9.10) називаються співвідношенням Кельвіна.

Таким чином, коефіцієнт термо-е.р.с. α_AB і термо-е.р.с. Е_АВ визначаються обома матеріалами А і В. Інтегрування рівняння (9.10) дає

α_AB = 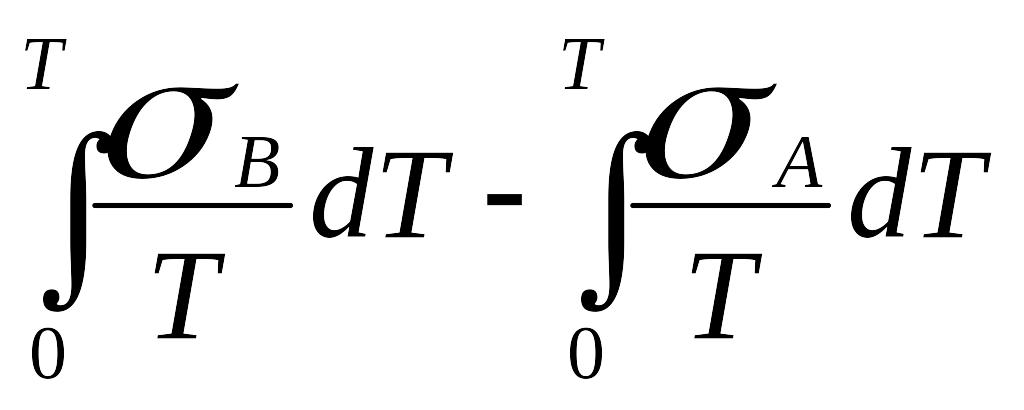(9.11)

де коефіцієнт α_AB приймається зникаюче малим при Т = 0.

Якщо абсолютну величину коефіцієнта термо-е.р.с. матеріалу А при температурі Т визначити як:

α_A = 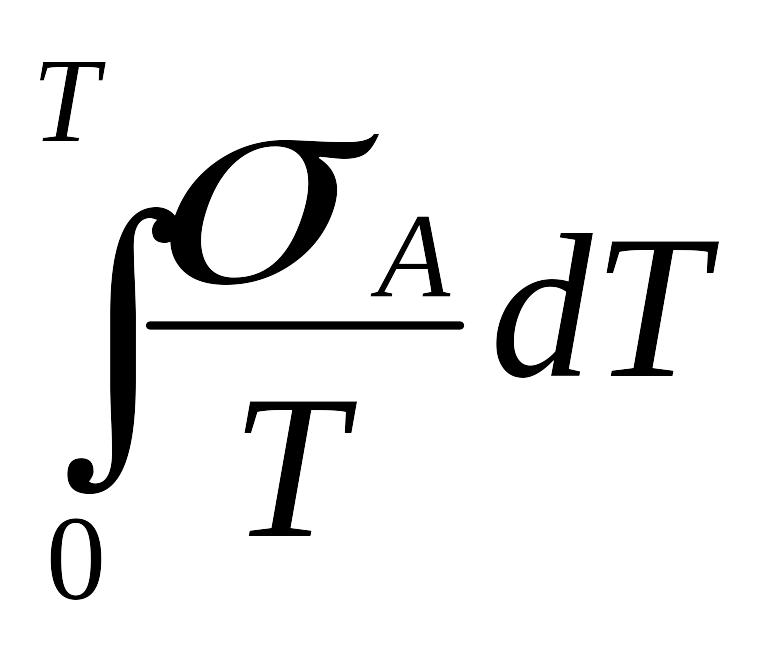(9.12)

то з (9.11) одержимо:

(9.13)

Із співвідношення (9.13) слідує, що коли відома абсолютна величина коефіцієнта термо-е.р.с. α одного матеріалу, прийнятого в якості еталона, то для будь-якого іншого матеріалу цей коефіцієнт легко одержати за допомогою вимірювань відносно цього еталону.

В свій час в якості еталонного матеріалу використовували свинець, оскільки його коефіцієнт Томсона і, відповідно, коефіцієнт Зеебека достатньо малі або рівні нулю. В останній час здебільше використовують платину, хоча вона і має значний коефіцієнт Томсона. Справа у тому, що платину можна виготовити із високою степеню чистоти, вона може використовуватись в більш широкому діапазоні температур і є поширеним матеріалом для термопар. Мідь також використовують для градуювання інших електродів порівняння, оскільки температурна залежність α_cu = f(Т) , одержана різними авторами, практично однакова.

Для більшості металів коефіцієнт α має порядок величини в межах 0...100 мкВ/°С, тоді як для напівпровідників він значно вищий, досягаючи в деяких випадках 1 мВ/°С.