4.4. Дослідження реологічних властивостей структурованих дисперсних систем

Серед різноманітних видів текучих речовин, в'язких рідин, пластично-в'язкої та твердо-пластичних систем за реологічними властивостями в стаціонарному потоці виділяють два основних класи речовин: 1 - ньютонівські рідини з величиною в'язкості, яка не залежить від дії на них напруг зсуву та градієнта швидкості і 2 - структуровані дисперсні системи, для яких величина в'язкості може змінюватись в широких межах, у залежності від діючої напруги зсуву та градієнта швидкості. Структуровані дисперсні системи займають проміжне положення між звичайними (ньютонівськими) в'язкими рідинами і пружніми твердими тілами. Для цього класу речовин характерні такі механічні властивості як в'язкість, пластичність, міцність, тощо. Саме ці властивості дисперсних систем без досліджень внутрішньої структури вивчає реологія, хоча і дозволяє визначити тип структури, що утворилась.

Багато будівельних матеріалів у процесі їх виготовлення проходять стадію тістоподібного або рідкотекучого (шлікерного) стану, тобто на певній технологічній стадії, найчастіше перед формуванням, вони являють собою технічні концентровані суспензії, або так звані, пластично-в'язкі системи. Такі суспензії, як правило, мають коагуляційні структури, які виникають у них під дією ван-дер-ваальсових сил зчеплення колоїдних частинок.

Текучість ідеальних в'язких рідин описується законом Ньютона, згідно якому сила внутрішнього тертя F (рівна по значенню, але обернена за напрямком прикладеній зовні силі) є пропорційна градієнту швидкості текучості dV/dx між шарами рідини, що знаходяться на відстані dx; та площі шару S, до якого прикладена зовнішня сила:

F= - dV/dx (4.23)

де  - коефіцієнт пропорційності, який називається в'язкістю або коефіцієнтом внутрішнього тертя і залежить від природи та термодинамічного стану рідини. Закон справедливий лише при ламінарній текучості, тобто коли всі шари рідини рухаються в паралельних напрямках. Для дослідження реологічних властивостей рідин рівняння (4.23) може бути записане у вигляді:

P=dV/dx (4.24)

Величина P= F/S (4.25) є прикладеною напругою зсуву.

В'язкі речовини відрізняються від пластичних тим, що текучість спостерігається при будь-яких прикладених напругах Р в тому числі і при Р = 0, а коефіцієнт внутрішнього тертя  є постійним (рис. 4.8).

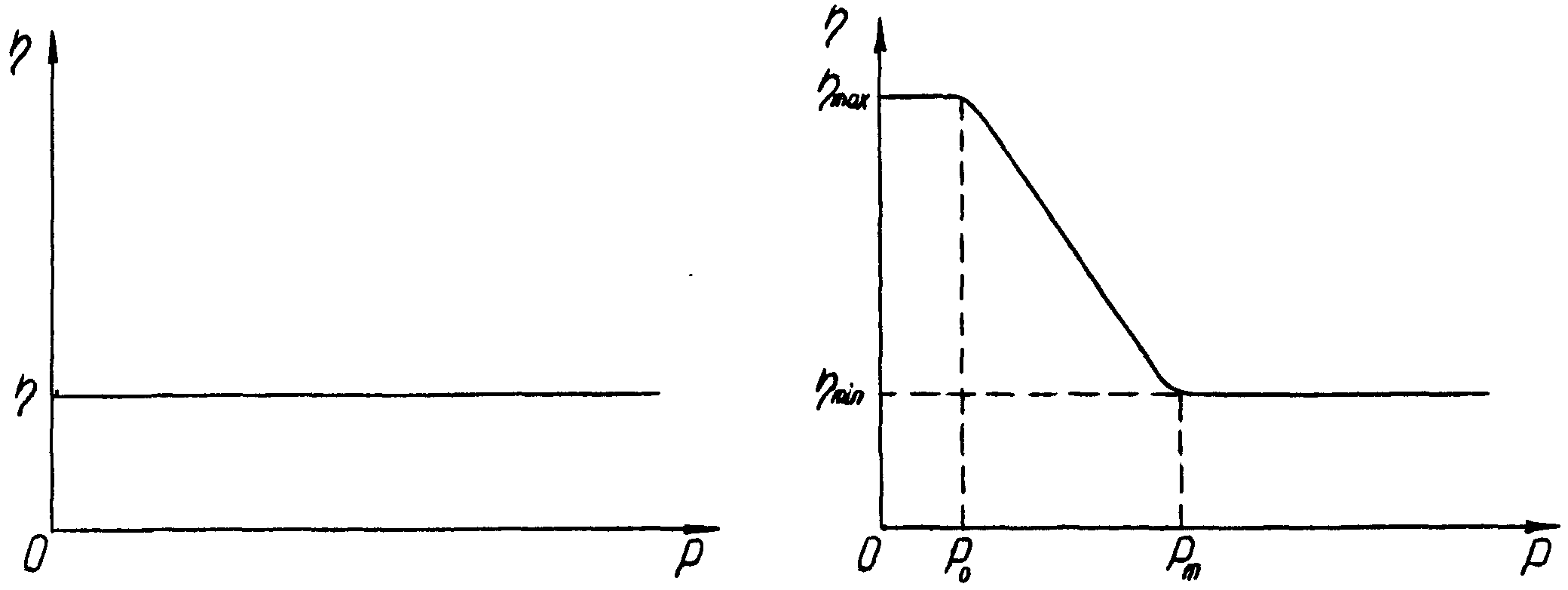
Рис. 4.8. Залежність в'язкості від напруг зсуву Р для ньютонівських рідин

Рис. 4.9. Залежність в'язкості від напруг зсуву Р для структурованих дисперсних систем (бігманівських рідин)

Структуровані дисперсні системи не підлягають закону Ньютона. Оскільки в процесі текучості в них відбувається руйнування структури, деформація і орієнтування в потоці частинок дисперсної фази, тому реологічна поведінка структурованих дисперсних систем більш складна. Із рис. 4.9 видно, що для не ньютонівських систем в'язкість не є постійною і зменшується в певній області напруг зсуву (P₀ – Pm). Так для суспензій бентонітових глин _max =10⁷ пуаз, а _min =10 пуаз (1 пуаз = 0,1 Нс/м² = 0,1Пас)

В області середніх руйнівних напруг (P₀ - Рm) реологічна поведінка структурованих дисперсних систем наближено описується рівнянням Бігмана:

P - P =  dV/dx (4.26)

де зовнішній тиск начебто розбивається на дві складові: Р^х - необхідний для руйнування структури і (Р - Р^х)- здійснення власної текучості;  - носить назву бігманівської в'язкості.

При Р > Рт відбувається текучість рідини із повністю зруйнованою дисперсною структурою речовини та з ейнштейнівською в'язкістю (4.27). В'язкість дисперсної системи золя, суспензії збільшується із зростанням кількості дисперсної фази і при умові, що між її частинками відсутня взаємодія, виражається законом Ейнштейна:



Рис. 4.10. Залежність в'язкості від напруг зсуву Р для твердоподібних систем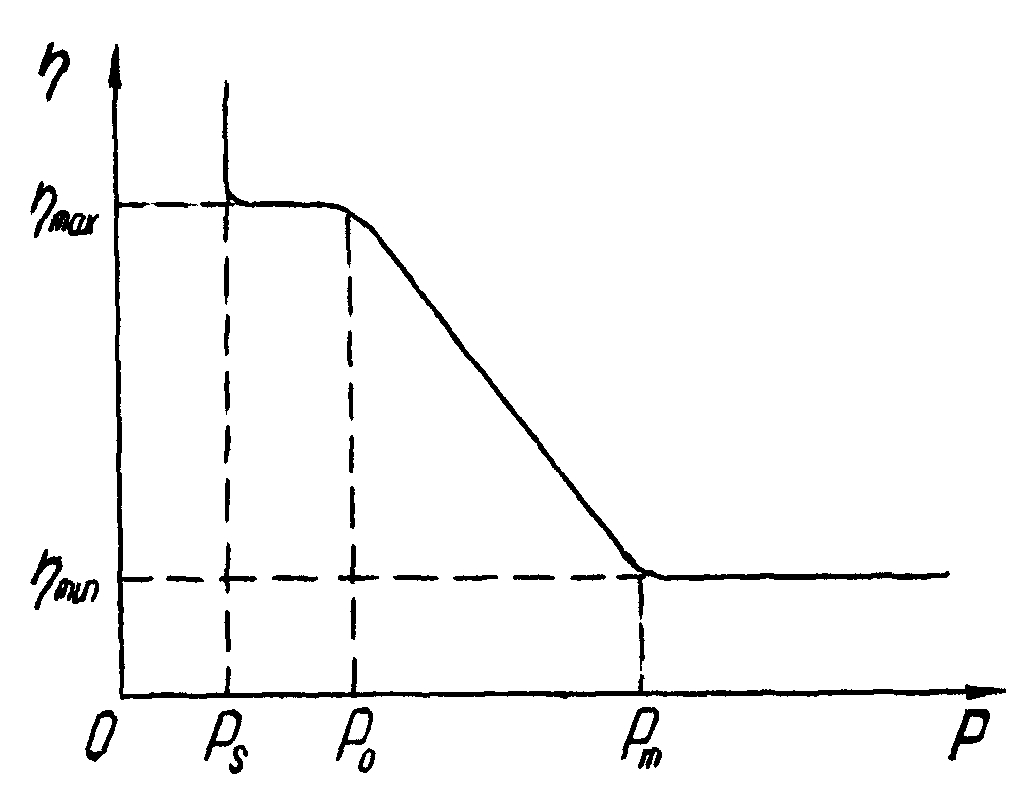

= (1+K) (4.27)

де  i  - в'язкість дисперсної системи і чистого дисперсійного середовища;  - об'ємна частина (доля) дисперсної фази; K - константа, яка визначається формою частинок (для сферичних K =2,5). Особливо характерне те, що в'язкість не залежить від власного розміру частинок.

Для дуже структурованих твердоподібних систем крива в'язкості має інший вигляд (рис. 4.10).

При Р<P текучості немає. Величина P називається першою граничною напругою зсуву і є близькою за змістом до межі пружності твердих тіл. Вона характеризує механічні властивості суцільної просторової ґратки, яка пронизує весь об'єм системи. При Р<Р_s можна рахувати структуровані системи твердоподібними.

При підвищенні напруг зсуву Р>Р₀ степінь руйнування структури збільшується і може досягнути найбільшої величини, на що буде вказувати значення найменшої в'язкості _min відповідно друга гранична напруга зсуву Рm, якими в даному випадку буде характеризуватись ця система. Найменша в'язкість системи із зруйнованою структурою вже не залежить від величини напруги зсуву і градієнта швидкості в умовах стаціонарного потоку, тобто при досягненні найменшої в'язкості система буде вести себе подібно до ньютонівської рідини. В'язкість, яка спостерігається в межах _min  носить назву ефективної в'язкості  або в'язкості гранично зруйнованої структури.

Таким чином, реологічні властивості пластично-в'язкого матеріалу можуть бути охарактеризовані в достатньо повній степені величиною першої граничної напруги зсуву Р і значенням найбільшої в'язкості _max та величиною найменшої напруги, яка відповідає повністю зруйнованій дисперсній системі другої граничної напруги зсуву P і значенню найменшої в'язкості _min при цьому. Окрім того, існує інтервал напруг зсуву від значення Р до Р , в якому величина в'язкості _max залишається постійною, Р - максимальна гранична напруга зсуву ще незруйнованої структури.