Практическая работа № 2 Построение эпюр крутящих моментов и определение диаметра вала из условий прочности и жесткости при кручении

Задание: Для стального вала круглого поперечного сечения определить значения

внешних моментов, соответствующих передаваемым мощ­ностям, и уравновешенный

момент (рис.2.7, табл.2.1). Построить эпюру крутящих моментов по длине вала.

Определить диаметры вала по сечениям из расчетов на проч­ность и жесткость.

Полученный больший результат округлить до ближайшего четного или

оканчивающегося на 5 числа. При расчете использовать следующие данные: вал

вращается с угловой скоростью ω = 25 рад/с; материал вала — сталь, [τ_k] = 30 МПа,

модуль упругости при сдвиге G = 8 • 10⁴ МПа; допускаемый угол закручивания

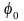[ ] = 0,02 рад/м. Провести расчет для вала кольцевого сечения, приняв с = 0,9. Сделать

выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив

п лощади поперечных сечений.

Дано: ω = 20 рад/с, Р₁ = 56 кВт, Р₂ = 28 кВт, Р₃ = 130 кВт

Решение:

1. Определяем вращающие моменты на шкивах.

М₁ = Р₁·ω = 56000·20 = 1120000 Н·м

М₂ = Р₂·ω = 28000·20 = 560000 Н·м

М₃ = Р₃·ω = 130000·20 = 2600000 Н·м

М = М₁ + М₂ + М₃ = 1940000 Н·м

2. Пользуясь методом сечений, определяем крутящие моменты на участках вала.

Сечение 1:

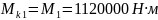
Сечение 2:

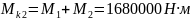
Сечение 3:

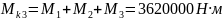
3. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т.к. моменты отрицательные. Максимальное значение крутящего момента на валу в этом случае 1940000 Н·м.

4. Выберем рациональное расположение шкивов на валу. Наиболее целесообразно такое размещение шкивов, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по возможности одинаковыми. Из этих соображений ведущий шкив, передающий момент 1940000 Н·м, помещают ближе к центру вала, ведомые шкивы 1 и 2 размещают слева от ведущего с моментом 1940000 Н·м, шкив 3 остается на том же месте. Строим эпюру крутящих моментов при выбранном расположении шкивов.

Максимальное значение крутящего момента на валу при выбранном расположении шкивов

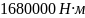
5. Определяем диаметр вала из условия прочности при условии, что сечение – круг. Условие прочности при кручении:

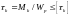
Момент сопротивления кручению:

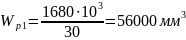
Определяем диаметр вала:

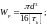
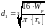
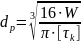
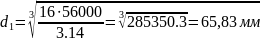
Округляя до ближайшего стандартного значения (СТ СЭВ 514-77), получаем

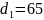мм

6. Определяем диаметр вала из условия жесткости

Полярный момент инерции

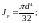
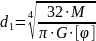
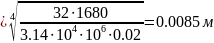
Округляя до ближайшего стандартного значения (СТ СЭВ 514-77), получаем

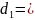
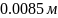
7. Определяем диаметры вала по сечениям при условии, что сечение - кольцо

Момент сопротивления остается тем же. По условию

Полярный момент сопротивления кольца:

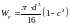
Формула для определения наружного диаметра вала кольцевого сечения:

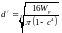
Расчет можно провести по формуле:

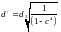
Диаметры вала по сечениям:

=

Наружные диаметры вала кольцевого сечения практически не изменились.

Для кольцевого сечения:, ,

8. Для вывода об экономии металла, при переходе на кольцевое сечение, сравним площади сечений.

При условии что сечение – круг

Сплошное круглое сечение:

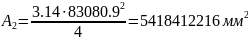
При условии, что сечение – кольцо,

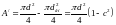
Кольцевое сечение:

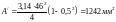
Сравнительная оценка результатов:

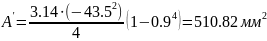
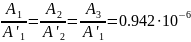
Следовательно, при переходе с кругового на кольцевое сечение экономия металла по весу составит 1,3 раза. Выбираем для вала кольцевое сечение.

Контрольные вопросы

1. Какие деформации возникают при кручении?

Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала значит длина и диаметр вала после скручивания изменяются.

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колос на валу?

Рациональное расположение колес — расположение, при кото­ром максимальное значение крутящего момента на валу — наи­меньшее из возможных

6. Что такое полярный момент инерции? Какой физический смысл имеет эта величина?

В каких единицах измеряется?

Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

7. Как вычисляют значение крутящего момента в поперечном сечении вала?

8. Что такое эпюра крутящего момента и как она строится?

При построений эпюр Мкр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.

9. Для чего строится эпюра крутящих моментов?

Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.

10. В чем заключается расчет на прочность при кручении?

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его прочности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

11. В чем заключается расчет на жесткость при кручении?