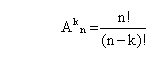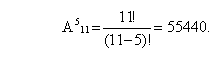1.Правила суммы и произведения в комбинаторике

Перейти к: навигация, поиск

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правила суммы и правила произведения.

Правило суммы

Правило суммы: если элемент А можно выбрать n различными способами и независимо от него элемент B можно выбрать m различными способами, то выбрать все различные комбинации элементов «A или B» можно n+m способами.

Объем множества Х мы будем обозначать |X|.

Пример: Школьникам на предстоящий зачет дается на выбор 5 тем по алгебре или 7 по геометрии. Сколькими способами можно выбрать тему по алгебре или геометрии?

Решение: |X|=5, |Y|=7. Множества не пересекаются, значит можно применить правило суммы: |X|+|Y|=5+7=12 способов.

Ответ: 12 способами ученик может выбрать тему.

Правило включений и исключений

Мы рассмотрели простейшие случаи, когда множества не пересекаются. А как быть с множествами, которые пересекаются? Для них существует правило включений и исключений.

Правило включений и исключений: если элемент А можно выбрать n различными способами и независимо от него элемент B можно выбрать m различными способами, причем множества элементов пересекаются, то выбрать все различные комбинации элементов «A или B» можно по формуле:

Графически правило включений и исключений можно представить так:

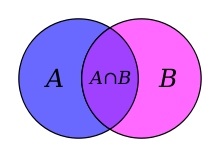
Правило произведения

Правило произведения: если элемент A можно выбрать n различными способами и независимо от него элемент B можно выбрать m различными способами, то все различные комбинации элементов «A и B» можно выбрать n*m способами.

Пример: На первой полке стоит 10 книг, а на второй 5. Сколькими способами можно взять книги с обеих полок?

Решение: |X|=10, |Y|=5. По правилу произведения: |X|*|Y|=10*5=50.

Ответ: 50 способами.

Правила суммы и произведения естественным образом обобщаются и на случай комбинаций многих элементов, а именно, если первый элемент совокупности из k различных элементов можно выбрать n1 способами, второй — n2 способами и так далее, k-й элемент — nk способами, то всевозможных комбинаций соответственно n1+n2+...+nk и n1*n2*...*nk.

Число размещений без повторений Теорема: Число размещений без повторений из n элементов по r A_n^r = n(n-1)(n-2)…(n-r+1) = n!/(n-r)!.

Доказательство: В r-размещении (а₁,a₂,…,a_r) n-элементного множества M элемент а₁ можно выбрать n способами. После этого элемент a₂ можно выбрать n-1 способами (из оставшихся n-1 элементов множества M). После этого элемент a₃ можно выбрать n-2 способами. И так далее. Наконец, элемент аr можно выбрать n-г+1 способами. По правилу произведения = n (n-1) (n-2)… (n-r+1); умножив и разделив правую часть равенства на (n-r)(n-r-1)…3*2*1. Получим A_n^r = n!/(n-r)!.

Следствие: Число перестановок n-элементного множества без повторений Pn = n!.

Число размещений с повторениями Теорема: Число размещений с повторениями A’_n^r = n^r.

Доказательство: В r-размещении (а₁, a₂,…,a_r) элемент а₁ в n-элементном множестве M можно выбрать n способами, элемент a₂ – тоже n способами, наконец, элемент a_r – n способами. По правилу произведения A’_n^r.

Следствие: Число перестановок с повторениями C_n^r = n!/(r!(n-r)!).

Число сочетаний без повторений Теорема: Число сочетаний без повторений C_n^r = n!/(r! (n-r)!).

Доказательство: Каждому r-сочетанию (а₁, a₂,…, a_r) n-элементного множества соответствует r! перестановок. Тогда число размещений A’_n^r = C_n^rr! откуда и следует требуемая формула.

Число сочетаний с повторениями Теорема: Число сочетаний с повторениями C’_n^r = C’_n+1-^r.

Доказательство: Каждому r-сочетанию из n-элементного множества M сопоставим набор (k₁, k₂,…, k_n) из натуральных чисел, указывающих число повторов каждого элемента из M в выбранном сочетании. При этом k₁ +k₂ +…+ k_n = r. Например, если M = {a,b,c,d,e}, то сочетанию (a,a,c,c,c,e,e) сопоставим набор (2,0,3,0,2), то есть элементы a,b,c,d,e множества M встречаются в сочетании (а,а,с,с,с,е,е) соответственно 2,0,3,0,2 раз. Каждому полученному набору (k₁, k₂, …, k_n) сопоставим набор (l₁, l₂,…,l_n), где l_i = k₁ +1, i = 1,2,…, n. Тогда l₁+l₂+…+l_n = k₁+k₂ +…+k_n +n = r+n. Каждый полученный набор (l₁, l₂, …, l_n) взаимнооднозначно соответствует числу n+r ненулевых слагаемых l₁, l₂,…,l_n. Разделим n+r последовательно записанных звездочек вертикальными разделительными черточками на n непустых частей, состоящих соответственно из l₁, l₂,…,l_n звездочек. Для нашего примера получим следующее разбиение: * * * | * | * * * * | * | * * * l₁ =3 l₂ =1 l₃ =4 l₄ =1 l₅=3 k₁ =2 k₂ =0 k₃ =3 k₄ =0 k₅=2

Каждому разбиению числа n+r на n ненулевых слагаемых взаимнооднозначно соответствует распределение n-1 разделителей, которые можно расставить в n+r-1 пробелах между звездочками C_n+r-1^n-1 способами. Следовательно, число сочетаний с повторениями C’_n^r = C_n+r-1.

Перестановка без повторении

Задача. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые начинаются цифрой 3?

РЕШЕНИЕ

1) Поставим цифру 3 на первое место и зафиксируем ее. А остальные четыре цифры будем переставлять для получения различных чисел. Таким образом, количество чисел будет определяться количеством перестановок среди чисел 1, 2, 4, 5. Чтобы его найти, воспользуемся формулой комбинаторики:

N = n! ,

де N – количество вариантов перестановок, n – количество цифр.

N = 4! = 24

ОТВЕТ: Из цифр 1, 2, 3, 4, 5 можно составить 24 пятизначных числа без повторения цифр, которые начинаются цифрой 3?

задача на формулу сочетаний

Задача. Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин. РЕШЕНИЕ Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков. ОТВЕТ: При данных условиях можно составить 55440 различных расписаний