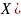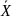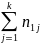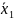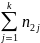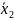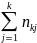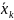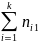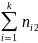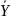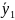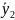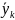- •Инструкция по выполнению курсовой работы.
- •Двухфакторный дисперсионный анализ с повторениями
- •Диалоговое окно Двухфакторный дисперсионный анализ с повторениями
- •Диалоговое окно Корреляция
- •Диалоговое окно Ковариация
- •Диалоговое окно Описательная статистика
- •Диалоговое окно Экспоненциальное сглаживание
- •Диалоговое окно Двухвыборочный f-тест для дисперсии
- •Диалоговое окно Анализ Фурье
- •Диалоговое окно Гистограмма
- •Диалоговое окно Скользящее среднее
- •Диалоговое окно Генерация случайных чисел
- •Диалоговое окно Ранг и персентиль
- •Диалоговое окно Регрессия
- •Диалоговое окно Выборка
- •Двухвыборочный t-тест с различными дисперсиями
- •Диалоговое окно Двухвыборочный t-тест с различными дисперсиями
- •Диалоговое окно Двухвыборочный z-тест для средних
- •Создание диаграммы рассеивания и построение линейной и параболической регрессии
- •Построение корреляционной таблицы
- •Полигоны, гистограммы, эмпирические функции распределения.
Построение корреляционной таблицы
Корреляционная таблица позволяет изложить материал сжато, компактно и наглядно.
Построение
корреляционной таблицы начинают с
группировки значений фактического и
результативного признаков. Для этого
надо разбить все данные значения на
требуемое количество интервалов (если
количество интервалов не оговаривается
в задании, можно выбрать k
= 7, 8 или 10). Длина интервала вычисляется
по формулам
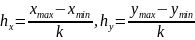 ,
где k
— количество интервалов. В первый
столбик следует вписать значения
факторного признака (X),
а первую строку заполнить значениями
результативного признака (Y).
,
где k
— количество интервалов. В первый
столбик следует вписать значения
факторного признака (X),
а первую строку заполнить значениями
результативного признака (Y).
|
[ymin, ymin + hy) |
[ymin + hy, ymin + 2hy) |
… |
[ymax - hy, ymax ] |
n(y) |
|
[xmin, xmin + hx) |
n11 |
n12 |
… |
n1k |
|
|
[xmin + hx, xmin + 2hx) |
n21 |
n22 |
… |
n2k |
|
|
… |
… |
… |
… |
… |
… |
… |
[xmax - hx, xmax ] |
nk1 |
nk2 |
… |
nkk |
|
|
n(x) |
|
|
… |
|
n |
|
|
|
|
… |
|
|
|
Числа
nij,
полученные на пересечении строк и
столбцов, означают частоту повторения
данного сочетания значений X
и Y,
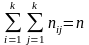 ,
где n
— объем выборки. Если nij
расположены в таблице беспорядочно,
можно говорить об отсутствии связи
между переменными. В случае образования
какого-либо характерного сочетания nij
допустимо утверждать о связи между Х
и Y.
При этом, если nij
концентрируется около одной из двух
диагоналей, имеет место прямая или
обратная линейная связь.
,
где n
— объем выборки. Если nij
расположены в таблице беспорядочно,
можно говорить об отсутствии связи
между переменными. В случае образования
какого-либо характерного сочетания nij
допустимо утверждать о связи между Х
и Y.
При этом, если nij
концентрируется около одной из двух
диагоналей, имеет место прямая или
обратная линейная связь.
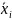 и
и
 — середины соответствующих интервалов.
Теперь можно пересчитать числовые
характеристики по сгруппированной
выборке, используя для этого формулы:
— середины соответствующих интервалов.
Теперь можно пересчитать числовые
характеристики по сгруппированной
выборке, используя для этого формулы:
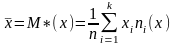 ,
,
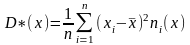 ,
,
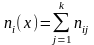 .
.
Полигоны, гистограммы, эмпирические функции распределения.
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Гистограммой
частот называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями
которой служат частичные интервалы
длиной h,
а высоты равны отношению
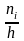 .
Площадь гистограммы частот равна сумме
всех частот, т.е. объему выборки n.
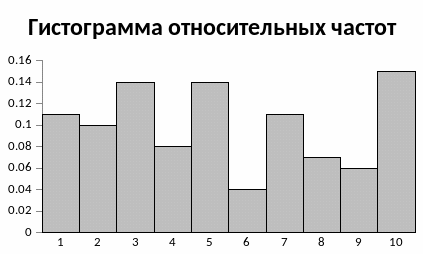
В случае гистограммы относительных
частот по оси ординат откладываются
нормированные относительные частоты
.
Площадь гистограммы частот равна сумме
всех частот, т.е. объему выборки n.
В случае гистограммы относительных
частот по оси ординат откладываются
нормированные относительные частоты
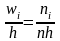 ,
на оси абсцисс – частичные интервалы.
Площадь гистограммы относительных
частот равна сумме всех относительных
частот, то есть единице.
,
на оси абсцисс – частичные интервалы.
Площадь гистограммы относительных
частот равна сумме всех относительных
частот, то есть единице.
Полигоном частот называют ломаную линию, отрезки которой соединяют точки (xi, ni), i=1, 2, … k. Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат – соответствующие им частоты ni и соединяют точки (xi, ni) отрезками прямых.
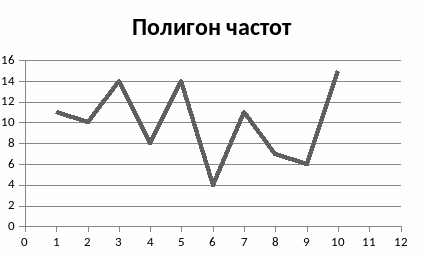
Полигон
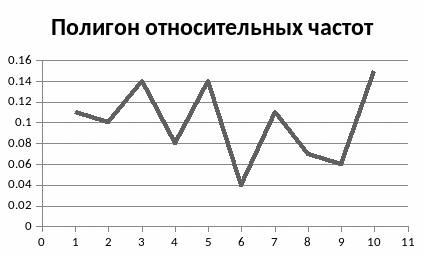
относительных частот строится аналогично,
за исключением того, что на оси ординат
откладываются относительные частоты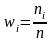 .
Для построения полигона нормированных
относительных частот на оси ординат
откладывают нормированные относительные
частоты
.
.
Для построения полигона нормированных
относительных частот на оси ординат
откладывают нормированные относительные
частоты
.
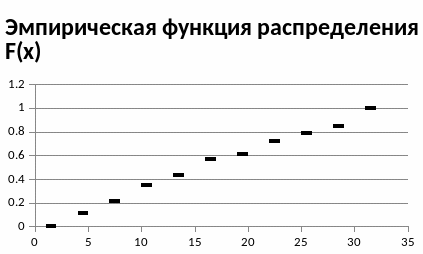
Эмпирической
функцией распределения называется
функция, вычисляемая для любого значения
х по
формуле
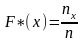 ,
где n –
объем выборки,
,
где n –
объем выборки,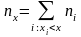 –
количество вариант, значения которых
меньше, чем х.
Для нашей выборки
–
количество вариант, значения которых
меньше, чем х.
Для нашей выборки
1)
F*(x)
= 0, для всех
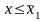 .
2)
.
2)
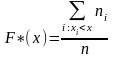 для
для
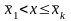
3)
F*
(x)
= 1, для всех
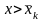 .
.
Откладывая
на оси абсцисс точки
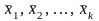 ,
а на оси ординат отрезки, параллельные
оси абсцисс, получим ступенчатую функцию:
,
а на оси ординат отрезки, параллельные
оси абсцисс, получим ступенчатую функцию: