Линеаризованное уравнение нелинейного элемента

U=2a I⁰i=ri, r=2a I⁰.

Рис. 2.7. Линеаризован- ная модель цепи по рис. 2.6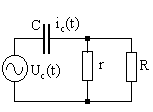

Полагая, что i_c(t)<< I⁰, заменим нелинейную цепь линеаризованной моделью (рис. 2.7). Теперь анализ такой цепи является достаточно простой задачей. Особенностью линеаризованных моделей цепей является то, что постоянные источники в них отсутствуют, поскольку их приращения равны нулю (источник постоянной ЭДС заменяется закороткой, источник постоянного тока - разрывом).

Рассмотрим алгоритм линеаризации некоторого абстрактного управляющего элемента (рис. 2.8).

Пусть имеются нелинейные зависимости

I₂=F(U_у, U₂), U_у=F( I_у). (2.7)

Рис. 2.8. Схема нели- нейного управляемого элемента

Проведем линеаризацию относительно режима покоя

I₂⁰, U₂⁰, U_у⁰.

Разложив зависимость (2.7) в ряд Тейлора, получим

(2.8)

=r₁₁ .

Оставляя пока без комментариев физический смысл коэффициентов линеаризованных уравнений S, r_i, r₁₁ на основании (2.8) можно построить электрическую линеаризованную модель управляемого элемента (рис. 2.9).

Рассмотрим пример использования линеаризованной модели для анализа усилительного устройства, изображенного на рис. 2.10.

Рис. 2.10. Схема усилительного устройства

За счет источника смещения Е_см через управляемый элемент задается ток покоя I₂⁰, а под воздействием сигнала U_c(t) этот ток получает полезное приращение I₂(U_c), которое и требуется определить.

Рис. 2.9. Линеаризованная электрическая модель управляемого элемента

Заменим схему нелинейного устройства на рис. 2.10 линеаризованной моделью этого устройства, для чего управляемый элемент заменим линеаризованной моделью, а источники постоянной ЭДС Е_см и Е_н закоротим (рис. 2.11). Ясно, что задача определения I₂(U_c) по такой схеме решается обычным методом электротехники.

Поскольку нелинейные зависимости (2.7) для конкретных управляемых элементов чаще всего задаются в виде статических (для постоянного тока) вольт-амперных характеристик, то коэффициенты линеаризованного уравнения могут быть найдены графически. Допустим, что для некоторого элемента зависимость

I₂=F(U_у, U₂)

Рис. 2.11. Линеаризованная модель усилительного устройства

задана графически (рис. 2.12).

Из уравнения (2.8) следует, например, что параметр

.

Рис 2.12. Графическое определение коэффициента линеаризованного уравнения

Условие U₂=0 означает, что приращения определяют при неизменном значении U₂⁰, определяющем режим покоя.

Из рис. 2.12 очевиден алгоритм определения S. Аналогично можно определить и другие параметры линеаризованной модели, используя их определения из 2.8 и соответствующие вольт-амперные характеристики.

2.4. Частотный анализ линеаризованных цепей

При частотном анализе определяется установившееся значение реакции цепи на гармоническое воздействие

x(t)=x_m sin  t.

Хотя реальные сигналы, действующие в электронных цепях, как правило, не являются гармоническими, тем не менее гармоническое воздействие широко используется как удобный тестовый сигнал. Гармонический сигнал является единственным физически реализуемым сигналом, который при прохождении через линейную цепь не меняет своей формы (меняется лишь амплитуда и появляется фазовый сдвиг, рис. 2.13).

Рис. 2.13. Реакция цепи на гармоническое воздействие

Сохранение формы облегчает анализ (определение реакции), сводя его к определению амплитуды и фазы выходного сигнала.

С другой стороны, определяя реакцию цепи на гармонические сигналы разных частот (от низких до высоких), можно определить степень инерционности (быстродействие) цепи, так как максимальная скорость изменения гармонического сигнала во времени пропорциональна частоте

x(t)=x_m sin t; = x_m cos t; = x_m.

При частотном анализе широко используется символический метод (метод комплексных амплитуд), при котором реальный гармонический сигнал

x(t)=x_m sin  t

заменяется символическим (физически не существующим) комплексным экспоненциальным воздействием

. (2.9)

Такая замена возможна только для линейной цепи, в которой справедлив принцип суперпозиции и проводится с целью замены дифференциального уравнения цепи алгебраическим.

Действительно, дифференцирование и интегрирование (2.9) по времени приводит к следующим очевидным результатам:

то есть к умножению или делению исходной функции на j.

Реакция цепи на символический сигнал ищется в виде

(2.10)

где - некоторый комплексный оператор.

Представляя в (2.10) в показательной форме

,

где () - аргумент , К() - модуль ,

получим

Таким образом, искомая реакция

Итак, определив , его модуль К(), аргумент (), задача решается однозначно.

Оператор называется амплитудно-фазовой частотной характеристикой цепи (АФЧХ), зависимость называется амплитудной частотной характеристикой (АЧХ), - фазовой частотной характеристикой (ФЧХ).

Очень важным является то обстоятельство, что параметры К() и () могут быть определены экспериментально для сколько угодно сложной цепи, что широко применяется на практике.

Продемонстрируем на простом примере алгоритм частотного анализа. Пусть имеется цепь, связь "вход-выход" которой описывается дифференциальным уравнением

.

Введем символические значения

,

подстановка которых в дифференциальное уравнение приводит к равенству

откуда получаем

Рис. 2.14. Графики АЧХ и ФЧХ

(2.11)

а окончательно

Рис. 2.15. Прохождение импульсного сигнала через цепь с “завалом” АЧХ в области высоких частот

На основе (2.11) можно построить график АЧХ и ФЧХ (рис. 2.14), по которому определяется реакция цепи на гармоническое воздействие любой частоты (_i).

Кроме того, АЧХ позволяет сделать вывод о том, что данная цепь плохо пропускает высокочастотные сигналы, то есть сложный сигнал, проходя через такую цепь, “потеряет” высокочастотные составляющие. На рис. 2.15 показано изменение формы сигнала при прохождении через цепь с АЧХ на рис. 2.14.