2.2. Линеаризация нелинейных уравнений

Рис. 2.3. Искажения выходного сигнала, вызванные нелинейностью характеристики “вход-выход” усилителя

На практике встречается широкий класс задач, когда нелинейность электронного элемента (устройства) не является принципиально необходимой и, даже более того, может оказаться вредной. Так нелинейность характеристики “вход-выход” усилителя приводит к искажению формы усиливаемого сигнала (нелинейные искажения), которое может оказаться неприемлемым, например, для качественно воспроизводимой музыки (рис. 2.3).

Ситуация изменится, если входной сигнал подать на вход усилителя на фоне постоянного пьедестала - напряжения смещения Е_см (рис. 2.4) так, чтобы размах сигнала не выходил за пределы практически линейного участка а-в.

Рис. 2.4. Подача входного сигнала на постоянном пьедестале – напряжении смещения

Из рис. 2.4 видно, что несмотря на сохранившуюся нелинейность характеристики усилителя, переменная составляющая выходного напряжения теперь линейно связана со входным сигналом U_вых(t)=kU_c(t),

В принципе для любого нелинейного элемента с характеристикой “вход-выход”

y=F(x)

для малых приращений относительно некоторого начального значения функции

y₀=F(x₀)

связь “вход=выход” может быть заменена линейной (рис. 2.5) связью для приращения

y=kx, (2.3)

Рис. 2.5. Замена нелинейной зависи- мости y=F(x) линейной для малых приращений y=kx относительно исходного значения y₀ , x₀

y=y-y₀, x=x-x₀.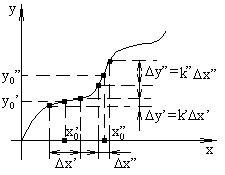

Хотя уравнение (2.3.) выглядит как линейное, оно называется линеаризованным, так как коэффициент уравнения k не является постоянной величиной, а зависит от начального значения y₀ функции

k=f (y₀ ).

Замена нелинейной связи y=F(x) линейной для приращений

y=kx

относительно некоторого исходного значения функции y₀=F(x₀) называется линеаризацией.

Значения y₀, x₀ называются режимом покоя нелинейного элемента. Поскольку коэффициенты линеаризованного уравнения (в том числе и дифференциального), а следовательно, и параметры устройства зависят от режима покоя - это понятие очень важно для электроники, а оптимальный выбор режима покоя является достаточно сложной оптимизационной многопараметровой задачей, поскольку характер зависимости отдельных параметров элемента от режима покоя может быть диаметрально противоположным.

Математически переход от нелинейного уравнения к линеаризованному осуществляется путем разложения нелинейной функции в ряд Тейлора в окрестности режима покоя с удержанием в этом разложении только приращения первого порядка.

Для электронного двухполюсника, описываемого на постоянном токе нелинейным уравнением

U=F(i), (2.4)

линеаризованное уравнение примет вид

(2.5)

Очевидно, что коэффициент k уравнения (2.5) имеет размерность сопротивления, которое принято называть дифференциальным сопротивлением или сопротивлением для приращений

U=ri. (2.6)

Переход от нелинейного уравнения (2.4) к линеаризованному (2.6) позволяет при анализе цепи для приращений заменить нелинейный двухполюсный элемент резистором, сопротивление r которого должно быть определено из статического режима.

Рассмотрим пример использования линеаризации для решения конкретной задачи.

На рис. 2.6 изображена схема, содержащая нелинейный элемент НЭ с характеристикой

Рис. 2.6. Нелинейная цепь

u=ai².

В схеме действуют два источника - постоянная ЭДС Е и переменный сигнал U_c(t) произвольной формы. Необходимо определить значение тока i_c(t), потребляемого от источника переменного сигнала.

Допустим, что графоаналитическим методом определено значение постоянного тока I⁰.