3.4.2. Акцепторная примесь

Рис. 3.3. Акцепторная примесь

Уровни этой примеси располагаются близко к потолку валентной зоны. Электроны валентной зоны ионизируют атомы примеси, создавая свободные носители - дырки, которые превалируют над электронами и являются основными носителями

p_P >> n_р.

Такой полупроводник называется дырочным, или р-типа. Уровень Ферми у него согласно (3.5) лежит ниже середины запрещенной зоны (рис. 3.3).

3.5. Р-п - переход

Р-п-переход - это область технологического контакта между слоями полупроводников п- и р-типа. Главной особенностью этого контакта является его ярко выраженная нелинейность - проводимость при одной полярности внешнего напряжения (прямое смещение) намного больше, чем при другой полярности (обратное смещение). И хотя р-п-переход может, как это будет показано, использоваться для разных целей, главное его применение - как элемента с преимущественно односторонней проводимостью (вентильного, выпрямительного элемента).

Рис. 3.4. Энергетическая диаграмма р-п-перехода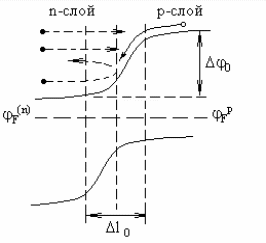

В основном для получения р-п-переходов используют примесные полупроводники с существенно различной концентрацией основных носителей. Рассмотрим пример, когда удельное сопротивление п-слоя значительно меньше, чем у р-слоя:

n_n>>p_n

соответственно на основании (3.4) для неосновных носителей верно обратное неравенство

p_n << n_р.

Поскольку уровень Ферми при равновесном состоянии твердого тела расположен горизонтально, то зонная диаграмма р-п-перехода приобретает вид, изображенный на рис. 3.4.

Хорошо видно, что разность уровня Ферми в п- и р-слоях приводит к энергетическому “искривлению” разрешенных зон: в области контакта появляется потенциальный барьер ₀.

Этот барьер создает поле, препятствующее переходу основных носителей из одного слоя в другой (пунктирная траектория электрона слоя п) и является ускоряющим для неосновных носителей (сплошная траектория для электрона слоя р). Искривление энергетической диаграммы распространяется на ширину l₀, составляющую порядка одного микрона. В этом промежутке свободных носителей практически нет: неосновные быстро “проскальзывают” его за счет дрейфа в ускоряющем поле потенциального барьера, а основные носители, диффузии которых барьер препятствует, практически туда не попадают. Этот участок на границе двух слоев, обладающий очень большим сопротивлением по сравнению с остальными участками п и р слоев собственно и называется р-п-переходом.

Рис. 3.6. Прямое смещение р-п-перехода

Рис. 3.5. Равновесное состояние р-п-перехода

В равновесном состоянии, когда внешнее напряжение, приложенное к р-п-переходу, равно нулю (рис. 3.5), малое число основных носителей, обладающих энергией, достаточной для преодоления потенциального барьера, уравновешивается встречным движением малого же числа неосновных носителей, свободно дрейфующим в поле перехода. В результате ток через переход равен нулю.

При прямом смещении, когда внешнее напряжение приложено такой полярностью, чтобы снизился потенциальный барьер, равновесие нарушается в сторону основных носителей, которыми обуславливается прямой ток I_n (рис. 3.6).

Зависимость величины прямого тока от приложенного напряжения U_п очень резкая, почти экспоненциальная. Следует обратить внимание на сужение области р-п-перехода, последствия которого будут рассмотрены далее.

При обратном смещении внешнее поле, суммируясь с полем потенциального барьера, делает практически нулевым поток основных носителей, в то время как дрейф неосновных носителей остается почти неизменным. Ток через переход меняет направление (рис. 3.7).

Обратный ток I₀ определяется неосновными носителями и поэтому очень мал. Ширина р-п-перехода в обратном включении возрастает.

Математическая связь между приложенным напряжением U_u, протекающим через р-п-переход током I определяется уравнением

(3.6)

где m - коэффициент, зависящий от материала полупроводника (для кремния m=2), I_S - обратный ток насыщения.

На основании (3.6) можно построить график зависимости I=F(U) -- вольт-амперную характеристику, из которого с очевидностью видна преимущественно односторонняя проводимость р-п-перехода (рис. 3.8).

При прямом смещении в (3.6) надо подставлять U>0, при обратном - U<0. Резкое нарастание прямого тока у кремниевых р-п-переходов наступает в районе 0.60.8В. Обратный ток при U₀>>m _т становится независимым от напряжения и равным I_S.

Значение I_S (на примере донорной примеси) соответствует числу неосновных носителей - дырок

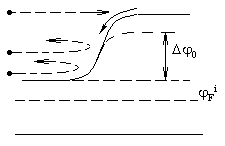Рис. 3.7. Обратное смещение р-п-перехода

где N_д = const - число атомов донорной примеси. Подставляя зависимость n_i от температуры и ширины запрещенной зоны (см. 3.2), получим

, (3.7)

I₀^’=const.

Рис. 3.8. Вольт-амперная характеристика р-п-перехода

Из (3.7) в силу неравенства  _з>>_Т следует резкая зависимость обратного тока от ширины запрещенной зоны (материала проводника). Так, у кремния при прочих равных условиях (концентрации примеси, геометрических размеров р-п-перехода) значение обратного тока почти на 3 порядка меньше, чем у германия.

Из (3.7) можно получить и зависимость I_S от температуры:

I_S(T)= I_S(T₀) e^T, (3.8)

где Т₀=300К (комнатная температура),   0.1 для кремния.

Соотношение (3.8) свидетельствует о резкой зависимости обратного тока от температуры.

Из (3.6) можно получить дуальное соотношение

. (3.9)

Пренебрегая единицей в (3.9), с учетом (3.7) можно записать:

. (3.10)

Из (3.10) следует практически линейная зависимость напряжения на р-п-переходе при прямом смещении от температуры.

Зависимости обратного тока и прямого напряжения от температуры следует учитывать при расчете температурных нестабильностей устройств на основе р-п-переходов. С другой стороны, эти зависимости можно использовать как полезные для построения твердотельных датчиков температуры. Конструктивно оформленный р-п-переход (герметичный корпус, внешние выводы) называется диодом.