Министерство образования Российской Федерации

Томский политехнический университет

В.М. Сергеев

ЭЛЕКТРОНИКА

Часть 1

Элементная база, аналоговые функциональные устройства

Учебное пособие

Томск 2000

УДК

Сергеев В.М. Электроника. Ч.1: Элементная база, аналоговые функциональные устройства: Учеб. пособие. – Томск: Изд. ТПУ, 2000. –128 с.

В пособии в лаконичной форме изложены основные задачи, решаемые электронной техникой, дискретные и интегральные компоненты, необходимые для их решения, основы физических процессов в электронных устройствах и их аналитическое описание. Каждая глава сопровождается резюме, подчеркивающим основные моменты. Пособие подготовлено на кафедре компьютерных измерительных систем и метрологии, соответствует программе односеместрового курса и предназначено для студентов Центра дистанционного образования.

Печатается по постановлению Редакционно-издательского Совета Томского политехнического университета.

Рецензент:

В. А Шалимов ‑ доцент кафедры телевидения и управления ТУСУР, кандидат технических наук.

Темплан 2000

© Томский политехнический университет, 2000

1. Задачи, решаемые электронной техникой, и элементы, необходимые для их решения

Научное определение электроники - изучение и практическое использование взаимодействия электронов с электромагнитным полем - мало о чем говорит. В то же время, всем понятно, что электроника - это телевидение и компьютеры, современные коммуникационные системы (Internet, например) и управление техническими объектами (от космических кораблей до детских игрушек), это медицинские аппараты, заменяющие важнейшие органы человека (как, например, вживляемые человеческие стимуляторы), и так далее. Применение электроники в современной цивилизации стало практически необъятным. Тем не менее ее возможности можно легко систематизировать, рассмотрев суть решаемых ею задач. По большому счету, таких задач две.

Первая - преобразование информации, представленной электрическими сигналами, с целью удобства ее передачи, приема, хранения или отображения.

Вторая - преобразование электрической энергии с целью удобства ее транспортирования или использования.

Информация, сигналы являются объектом изучения в специальных курсах. Здесь же мы затронем лишь представления о них, минимально необходимые для изучения курса основ электроники.

Любая задача преобразования как информации, так и электрической энергии требует для ее решения широкого круга специальных знаний. В этой главе даются самые первые представления об этих проблемах с тем, чтобы у читателя возникло системное представление о предмете электроники и понимание необходимости изучения последующих разделов данного курса.

1.1. Электрические сигналы. Временное и спектральное представление

Информация - это сообщение о новом событии, передаваемом от источника к потребителю информации, в качестве которого могут выступать как люди, так и аппараты.

В электронике носителями информации являются электрические сигналы - изменение во времени параметров электромагнитного поля.

Далее будут рассматриваться сигналы в виде изменения во времени электрического напряжения (тока).

Аналитически сигналы можно описать двумя способами: представлением во временной области (функция времени) - S(t) или разложением в виде суммы элементарных колебаний (спектра).

Важнейшей характеристикой сигнала во временном представлении является его периодичность. Периодом сигнала Т является отрезок времени, для которого справедливо равенство

Рис. 1.1. Временное представление периодического сигнала

пилообразной формы

S(t+nT) = S(t), n=0,1,2,...

На рис. 1.1 изображен периодический сигнал пилообразного типа

.

На рис. 1.2 изображен гармонический сигнал с начальной фазой .

.

Рис. 1.2. Временное представление гармони- ческого сигнала с начальной фазой 

Спектральное представление сигнала в виде суммы элементарных колебаний может быть приведено с помощью широкого класса полиномов и функций: Лежандра, Чебышева, Лагерра, Эрмита, Хаара, Радемахера, Уолша и др.

Однако для спектрального представления периодических сигналов наибольшее практическое применение нашло разложение в виде суммы гармонических составляющих (гармоник) - ряда Фурье:

, (1.1)

где – круговая частота первой гармоники.

Коэффициенты a_n, b_n вычисляются по формулам:

Амплитуда A_n и фаза _n n-гармоники выражаются через a_n и b_n:

.

Совокупность коэффициентов A_n ряда Фурье называется частотным спектром периодического сигнала.

Как следует из (1.1) частотный спектр периодического сигнала носит дискретный характер, так как состоит из отдельных “линий” высотой A_n, соответствующих дискретным частотам 0, ₁, ₂, ₂=2₁, ₃=3₁ и т.д. (рис. 1.3).

Рис. 1.3. Пример частотного спектра сигнала

Хотя ряд Фурье и содержит бесконечное число гармоник, амплитуды этих гармоник у большинства реальных сигналов убывают с увеличением номера гармоник n. Физически это означает, что влияние высших гармоник на общую энергию сигнала и его форму может быть незначительным, что позволяет при анализе искусственно “урезать” спектр, ограничившись наиболее “влиятельными” низкими гармониками.

Частотный спектр пилообразного напряжения, изображенного на рис. 1.1, имеет вид

Рис. 1.4. Форма пилообразного сигнала при удержании пяти первых гармоник спектра

Как видно, амплитуды гармоник убывают с частотой по закону 1/n. При “удержании” в спектре, например, пяти первых гармоник форма сигнала принимает вид, изображенный на рис. 1.4 (сплошная линия), для многих случаев такая погрешность представления сигнала может оказаться приемлемой.

К сожалению, чем больше скорость изменения сигнала во времени, тем медленнее снижаются амплитуды гармоник по мере увеличения n. Для периодической (с периодом Т) последовательности прямоугольных импульсов с амплитудой Е и длительностью  амплитуда n-ой гармоники определяется по соотношению

и при , когда sinx х

то есть амплитуды всех гармоник (от 0 до ) становятся одинаковыми, спектр становится равномерным.

Увеличение ширины спектра при увеличении скорости изменения сигнала является основным препятствием для увеличения скорости передачи информации по каналам связи.

Разложение сигнала на гармонические составляющие (ряд Фурье) нашло широкое практическое применение по той причине, что гармоническое колебание является единственным физически существующим сигналом, форма которого не меняется при прохождении через линейную цепь (изменяется только амплитуда и фаза). Это свойство делает возможным при определении установившейся реакции цепи на гармоническое воздействие применение удобного символического метода - метода комплексных амплитуд.

Рис. 1.5. Возможный вид АЧХ цепи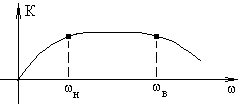

Как известно из электротехники, амплитуду выходного гармонического колебания можно определить по амплитудно-частотной характеристике цепи (АЧХ), которая может быть определена как аналитически, так и (что очень важно для сложных цепей) экспериментально. АЧХ - это зависимость

отношения амплитуды выходного и входного колебания (К) от частоты, которая может, например, иметь вид, представленный на рис. 1.5.

В пределах полосы частот (от _н до _в) АЧХ имеет равномерный характер. Это значит, что все гармоники сложного сигнала, “умещающегося” на этом частотном отрезке, пройдут через цепь практически с одинаковым усилением (или ослаблением, если К<1), что приведет лишь к изменению масштаба сигнала, а форма его останется неизменной. Если же полоса равномерной передачи цепи много меньше ширины спектра входного сигнала, то сигнал пройдет через такую цепь с большими искажениями, называемыми частотными.

Так, если через цепь, имеющую АЧХ (рис. 1.5), пропустить периодическую последовательность прямоугольных импульсов S₁(t), то выходной сигнал S₂(t) будет значительно отличаться по форме от входного (рис. 1.6).

Рис. 1.6. Искажения сигнала, прошедшего через цепь с “узкой” полосой пропускания

Таким образом, введение понятия частотного спектра сигнала позволяет сопоставить свойства канала связи (его широкополосность) с шириной спектра сигнала. Например, телевизионный сигнал, ширина спектра которого превышает 1010⁶Гц, невозможно передать по телефонной проводной паре, полоса пропускания которой составляет всего несколько десятков килогерц.

Для непериодического сигнала можно при анализе полагать Т. Это означает, что как значение частоты первой гармоники, так и интервал между соседними гармониками будет стремиться к нулю, т.е. спектр становится сплошным, а амплитуды гармоник (коэффициенты ряда Фурье) станут бесконечно малыми.

Рис. 1.7. Спектральная плотность S() одиночного импульса

Предельный переход от дискретного ряда Фурье к сигналу с Т описывается интегралом Фурье

,

где - спектральная плотность, физически означающая распределение мощности сигнала по диапазону частот.

На рис. 1.7 для примера приведена спектральная плотность одиночного импульса с амплитудой А и длительностью t_и.