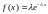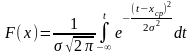111Equation Chapter 1 Section 1

1. Общие положения

1. Целью проведения практических занятий является овладение научными методами анализа, систематизация и обобщение теоретических знаний, приобретенных при изучении лекционного материала по дисциплине «Вероятностно-статистические модели эксплуатации ЛА»; приобретение навыков и умений применять теоретические знания к решению практических задач, возникающих при эксплуатации летательных аппаратов.

2. Практические занятия включают решения задач по всем основным темам дисциплины: формирование вероятностно-статистической модели и проверка ее соответствия экспериментальным данным с помощью критериев согласия; проведение точечной и интервальной оценок характеристик случайных величин объектов эксплуатации; анализ различных моделей изменения параметров объектов и характеристик процессов их функционирования; формирование моделей статистического контроля объектов; анализ марковских и полумарковских процессов эксплуатации объектов.

3. Пособие по каждому практическому занятию содержит название темы и цель занятия, краткие теоретические сведения по теме занятия и собственно задание для самостоятельной работы. По каждому занятию предусмотрено несколько вариантов исходных данных. Кроме того, преподаватель может выдать студентам дополнительные варианты.

4. По результатам выполнения каждого практического занятия студентом составляется отчет. Отчет должен содержать тему занятия, исходные данные выполненного варианта, необходимые теоретические зависимости, результаты расчетов в виде таблиц или графиков и выводы. В каждом отчете студент проставляет дату выполнения работы, указывает номер группы, свою фамилию и подписывает отчет.

2. Практические занятия

   1. Практическое занятие №1.

Тема: Формирование вероятностно-статистической модели с использованием законов распределения непрерывных случайных величин.

Цель работы: Приобрести навыки формирования вероятностно-статистических моделей на основе непрерывных законов распределения случайных величин.

1. Необходимые теоретические сведения

Для формирования вероятностно-статистических моделей объектов эксплуатации ЛА применяют следующие законы распределения непрерывных случайных величин: нормальный, экспоненциальный и Вейбулла.

Исходным материалом создания модели являются статистические данные, отражающие характер функционирования и особенности эксплуатации летательных аппаратов. Этот исходный материал представляет собой совокупность значений случайных величин: X₁, X₂, …X_n.

Первой операцией статистической обработки результатов является построение вариационного ряда – расположение совокупности чисел в порядке возрастания. Затем статистические данные необходимо сгруппировать в интервалы. Приближенная оценка длины интервала может быть сделана по следующей формуле

212\* MERGEFORMAT (.)

Используя сгруппированные данные, строят гистограмму плотностей распределения и гистограмму частостей.

Значение статистической плотности распределения в некотором i-м интервале рассчитывается по формуле:

313\* MERGEFORMAT (.)

где - число членов выборки, попавших в i-й интервал.

Частость, отражающая вероятность нахождения случайной величины X в i-м интервале, равна

414\* MERGEFORMAT (.)

По виду гистограммы, сравнивая ее с графиками плотностей распределений, приведенных в таблице 1.1, делают предположение о виде закона распределения, т. е. формируют вероятностно-статистическую модель рассматриваемого процесса эксплуатации.

Следующим шагом является определение параметров выбранной в качестве модели эмпирической функции распределения – математического ожидания m и дисперсии Д (среднеквадратического отклонения ). Эти величины определяются методом моментов с использованием гистограммы частостей.

Математическое ожидание исследуемой случайной величины есть начальный момент первого порядка

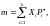515\* MERGEFORMAT (.)

где k – число интервалов разбиения вариационного ряда,

X_i – расстояние от середины i-го интервала до начала координат.

Дисперсия, характеризующая разброс случайной величины около математического ожидания, есть центральный момент второго порядка

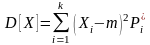616\* MERGEFORMAT (.)

Как известно,

717\* MERGEFORMAT (.)

Для завершения формирования вероятностно-статистической модели необходимо определить параметры теоретического закона распределения, принятого в качестве математического выражения модели.

Экспоненциальный закон распределения (см. табл. 1.1) определяет один параметр - , при этом

818\* MERGEFORMAT (.)

Нормальный закон распределения определяется двумя параметрами: математическим ожиданием m и среднеквадратическим отклонением , определенными методом моментов в соответствии с формулами (1.4), (1.5) и (1.6).

Распределение Вейбулла является двухпараметрическим: величина a есть параметр масштаба и величина b – параметр формы распределения. Чтобы определить эти величины необходимо воспользоваться таблицей 1.2. Сначала определяется коэффициент вариации

919\* MERGEFORMAT (.)

По таблице 1.2 для этого значения коэффициента вариации определяется значение параметра b и значения величин K_b и C_b. Параметр a определяется по формуле

10110\* MERGEFORMAT (.)

или по формуле

11111\* MERGEFORMAT (.)

2. Варианты заданий

Статистические данные наработки до отказа

элементов авиационной техники (в часах)

1 вариант	70	133	178	212	283	317	420	460	500	532
	595	645	742	788	822	856	929	995	1079	1126
	1193	1279	1366	1432	1497	1624	1719	1863	2195	2730
2 вариант	43	127	165	203	278	296	412	449	495	514
	576	638	696	776	803	852	921	995	1072	1124
	1180	1275	1346	1393	1454	1617	1709	1833	1968	2652
3 вариант	31	61	92	121	149	180	209	238	266	295
	322	350	377	400	469	509	554	599	644	688
	700	732	776	790	800	868	936	1003	1069	1136
	1200	1302	1402	1501	1600	1748	1883	2000	2200	2400
4 вариант	46	91	138	181	223	270	313	357	399	442
	483	525	565	600	703	763	831	898	966	1032
	1050	1098	1164	1185	1200	1302	1404	1504	1603	1704
	1800	1953	2103	2251	2400	2622	2824	3000	3300	3600
5 вариант	20	60	120	180	250	300	320	350	370	410
	460	520	650	700	720	750	780	850	900	950
	1000	1100	1130	1180	1250	1300	1350	1400	1500	1550
	1650	1700	1750	1850	1950	2050	2100	2150	2250	2300
	2500	2600	2650	2750	2850	2950	3000	3250	3500	3950
6 вариант	10	15	17	20	22	25	25	26	30	32
	32	39	41	42	45	45	47	50	52	53
	54	59	60	60	62	64	65	67	67	73
	73	74	74	77	78	79	84	85	86	89
	89	90	92	93	93	96	96	99	100	100
7 вариант	20	50	60	100	150	180	200	250	300	320
	330	350	360	370	380	410	460	520	550	600
	650	700	720	750	780	800	850	900	650	1000
	1100	1130	1180	1250	1300	1350	1400	1500	1550	1650
	1750	1850	1950	2050	2150	2300	2500	2850	3500	3200
8 вариант	50	120	190	250	330	350	420	490	560	630
	700	750	770	810	870	940	1000	1050	1080	1150
	1190	1210	1270	1330	1310	1460	1520	1560	1610	1680
	1760	1820	1900	1910	2050	2120	2200	2280	2350	2410
	2530	2650	2700	2710	2820	2950	3180	3320	3550	3900

Статистические данные замеров времени выполнения работы

путем хронометража (в часах)

9 вариант	Замена передней ноги шасси
	3,4	3,5	3,5	3,6	3,6	3,6	3,7	3,7	3,7	3,7
	3,8	3,8	3,8	3,8	3,8	3,9	3,9	3,9	3,9	3,9
	3,9	4,0	4,0	4,0	4,0	4,0	4,0	4,0	4,0	4,1
	4,1	4,1	4,1	4,1	4,1	4,2	4,2	4,2	4,2	4,2
	4,3	4,3	4,3	4,3	4,4	4,4	4,4	4,5	4,5	4,6
10 вариант	Замена двигателя (без его опробования и облета самолета)
	2,1	2,2	2,2	2,25	2,25	2,25	2,3	2,3	2,3	2,3
	2,4	2,4	2,4	2,4	2,4	2,44	2,44	2,44	2,44	2,44
	2,44	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,5	2,6
	2,6	2,6	2,6	2,6	2,6	2,64	2,64	2,64	2,64	2,64
	2,7	2,7	2,7	2,7	2,75	2,75	2,75	2,8	2,8	2,9

Таблица 1.1. Характеристики некоторых законов распределения

Наименование закона распределения	Параметры	Математические выражения		График
		плотности распределения	функции распределения		плотности распределения	функции распределения
Экспоненциальный
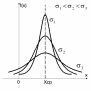
Нормальный	Хср σ
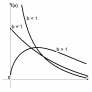
Вейбулла	a b

Таблица 1.2