7. Консервативные и неконсервативные силы.

Определение: Консервативными называются силы, работа которых не зависит от пути

перемещения, а определяется только начальной и конечной конфигурациями системы.

Таким образом, работа консервативных сил не зависит от пути перехода. Сила тяжести - консервативная

сила.

Можно ввести другое определение консервативных сил: работа консервативных сил по замкнутому

контуру равна 0. Легко увидеть, что это эквивалентное определение, рассмотрев работу по произвольной

замкнутой траектории.

Поле центральных сил.

Сила называется центральной, если она направлена к одной и той же точке (или от

нее) и зависит от расстояния до этой точки, которую называют силовым центром.

Выводы: работа центральных сил не зависит от пути перехода. Все центральные силы консервативны.

Неконсервативные силы.

К неконсервативным силам относятся все остальные силы. Среди них выделяют диссипативные и

гироскопические силы.

1) Диссипативные силы.

Силы трения. Важно, что для замкнутой

системы работа диссипативных сил всегда отрицательна, т.к. направление силы всегда против направления

перемещения или скорости.

Итак, определение: диссипативными называются такие силы, полная работа которых при любых

движениях в замкнутой системе всегда отрицательна.

2) Гироскопические силы.

Гироскопические силы зависят от скорости движения материальной точки и действуют

перпендикулярно этой скорости. Работа этих сил всегда равна нулю. Примеры гироскопических сил – сила.

Неупругие столкновения - это такие столкновения, при которых часть кинетической энергии переходит

во внутреннюю. Степень неупругости зависит от того, какая часть энергии переходит во внутреннюю. В

качестве примера - пуля пробивает доску и теряет часть энергии, которая идет на изменение внутренней

структуры и теплоту. Так, абсолютно неупругий удар - когда оба тела

сливаются в одно общее. При этом выполняется закон

сохранения импульса, а в законе сохранения энергии необходимо

учитывать, что часть кинетической энергии удара переходит во

внутреннюю энергию частиц.

1.14.3. Упругие столкновения

Столкновение двух частиц называется упругим, если оно не сопровождается изменением их

внутреннего состояния. В законе сохранения энергии внутреннюю энергию тел можно не учитывать.

9.Вращение твердого тела. Разобьем вращающееся тело на малые элементы Δm_i. Расстояния до оси вращения обозначим через r_i, модули линейных скоростей – через υ_i. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина 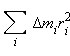зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

В пределе при Δm → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг·м²). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.

В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы.

Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I_C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела. Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δm_i – некоторый малый элемент массы твердого тела. По определению момента инерции:

Выражение для I_P можно переписать в виде:

Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно, I_P = I_C + md²

где m – полная масса тела. Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения).

Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δm_i. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть Ее можно разложить на две составляющие: касательную составляющую и радиальную Радиальная составляющая создает центростремительное ускорение a_n.

Касательная составляющая вызывает тангенциальное ускорение массы Δm_i. Второй закон Ньютона, записанный в скалярной форме, дает Δm_ia_iτ = F_iτ = F_i sin θ  или  Δm_ir_iε = F_i sin θ,

где – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r_i, то мы получим:

Здесь l_i – плечо силы , M_i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге: Iε = M.

Это и есть основное уравнение динамики вращательного движения твердого тела.

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L: L = Iω.

11.

15. Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как а = - w²·х,  то согласно II закону Ньютона справедливо следующее равенство: F = m·a = - m·w²·х = - k·x,   где k - постоянная величина. На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд: |F(x)| = k·x + k₁·x² + k₂·x³ + ... и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться. Уравнение динамики собственных колебаний. Рассмотрим колебания груза на пружине, считая, что вся масса сосредоточена в грузе, а упругость - в пружине. При х = 0 пружина не деформирована (см. рис. 10.1). Предположим, что сила трения в системе отсутствует F_тр = 0. В случае смещения тела от положения равновесия возникает сила упругости, действующая на тело и стремящаяся возвратить его в положение равновесия. Поскольку при малых деформациях х эта сила равна F = - k·x, то уравнение динамики движения груза согласно II закону Ньютона можно записать в виде: m·a = - k·x.      (10.2) Поскольку ускорение - есть вторая производная от координаты по времени, то решив дифференциальное уравнение (10.2), найдем зависимость x(t). В теории дифференциальных уравнений показано, что общим решением уравнений типа x'' + w₀²·x = 0 выражается зависимостью вида: x = A·cos(w₀·t + ₀). Можно рассуждать также следующим образом. Из (10.2) имеем, что для гармонических колебаний a = - w₀²·x, т.е. ускорение а пропорционально х и направлено в противоположную к нему сторону. Следовательно, колебания груза в случае выполнения условия (10.2) являются гармоническими и описываются уравнением:x = A·cos(w₀·t + ₀),    (10.3) где w₀ = (k/m)^1/2 - собственная частота колебаний.

Значение w₀ зависит только от физических свойств системы и не зависит от начальных условий.Физический маятник. Физическим маятником называется система, способная совершать колебания около положения равновесия, при этом массу системы нельзя считать сосредоточенной в одной точке. Введем обозначения: O - точка вращения; С - положение центра масс маятника; l - его длина;  - угол отклонения от положения равновесия. Уравнение динамики вращательного движения для физического маятника в проекции на ось вращения в случае его малых колебаний запишем в виде:M_z = ·'' = - m·g·l·sin = - m·g·l·.Решение этого уравнения имеет следующий вид:(t) = _max·sin(w₀·t + ₀), где w₀ = (m·g·l/I)^1/2.Для математического маятника момент инерции и значение собственной частоты колебаний будут равны: I = m·l² и  w₀ = (g/l)^1/2.Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:w₀ = (g/l_прив)^1/2, где l_прив = I/(m·l) - приведенная длина маятника.

Математический маятник.

Математический маятник- подвешенный к тонкой нити груз, размеры которого много меньше длины нити, а его масса много больше массы нити (т.е. груз можно считать материальной точкой, а нить невесомой).

Колебания груза на пружине.

Система, состоящая из тела, скрепленного с пружиной. После выведения этой системы из состояния равновесия пружина окажется деформированной, а на тело будет действовать сила упругости- тело будет колебаться.

12. Колебаниями или колебательными движениями являются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени. Колебания весьма разнообразны по своей природе: колеба­ния пружинного маятника, качания маятников, колебания струн, вибра­ции фундаментов, качка корабля, колебания ветвей деревьев и т.д.

Гармонические колебания- колебания, при которых величина смещения тела от положения равновесия с течением времени подчиняется законам: x=Asin(t+₀), x=Acos(t+₀).

Закон свободных гармонических колебаний: x=Asin(t+₀), x=Acos(t+₀); =x(t)=Аcos(t+₀); a=(t)=-А²sin(t+₀).

Гармонические колебания характеризуют:

1)период- время одного полного колебания; T=2m/k, T=2l/g;

2)амплитуда- максимальное смещение от положения равновесия;

3)частота- число полных колебаний за единицу времени. 1Герц (Гц)- частота такого колебательного движения, при котором колеблющееся тело совершает одно полное колебание за одну секунду.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени: положение маятника в часах, Т – период, v = 1/T.

При изучении кинематики колебательных движений нас интересуют:

- закон, по которое повторяется движение;

- время, через которое тело (система) снова приходит к тому же самому состоянию;

- наибольшие отклонения, которых достигает движущееся тело и т.д.

Изучив эти характеристика колебательного движения, мы можем определить состояние тела (системы) в любой момент времени.

При колебательном движении тела вдоль прямой линии (ось OX), вектор скорости направлен всегда вдоль этой прямой. Скорость υ = υ_x движения тела определяется выражением:

В математике процедура нахождения предела отношения при Δt → 0 называется вычислением производной функции x(t) по времени t и обозначается как или как x'(t), или, наконец, как . Для гармонического закона движения x = x_m cos (ωt + φ₀). Вычисление производной приводит к следующему результату:

Появление слагаемого + π / 2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости υ = ωx_m достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях:

следовательно, ускорение a равно производной функции υ(t) по времени t, или второй производной функции x(t). Вычисления дают:

Знак минус в этом выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, по 2-му закону Ньютона сила, заставляющая тело совершать гармонические колебания, направлена всегда в сторону положения равновесия (x = 0).

10. Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L: L = Iω.

Поскольку уравнение вращательного движения можно представить в виде:

Окончательно будем иметь:

Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.

Если суммарный момент М внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется: ΔL = 0, если M = 0.

Следовательно, L = Iω = const

Это и есть закон сохранения момента импульса. Закон сохранения момента импульса справедлив для любой замкнутой системы тел. Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца .

Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением.

Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением

Ось вращения O проходит через центр масс тела. Моменты силы тяжести и силы реакции относительно оси O равны нулю. Момент M создает только сила трения: M = F_трR.

Уравнение вращательного движения:

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I_C – момент инерции относительно оси O, проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде: ma = mg sin α – F_тр.

Исключая из этих уравнений F_тр, получим окончательно:

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара а у сплошного однородного цилиндра Следовательно, шар будет скатываться быстрее цилиндра.

8. Вращательное движение. Другим простейшим видом механического движения является вращательное движение абсолютно твердого тела. При таком движении его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на одном прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.

Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением. Угол поворота φ - это угол, считанный между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения.

Угловая скорость ω - векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первом производной от угла поворота по времени.

Н аправление вектора ω совпадает с направлением аксиального вектора Δφ, т.е. такого, который имеет длину численно равную углу Δφ в определенном масштабе, а направление совпадающее с осью вращения и определяемое правилом правого винта.

Н аправление вектора ω совпадает с направлением аксиального вектора Δφ, т.е. такого, который имеет длину численно равную углу Δφ в определенном масштабе, а направление совпадающее с осью вращения и определяемое правилом правого винта. Н аправление вектора ω совпадает с направлением аксиального вектора Δφ, т.е. такого, который имеет длину численно равную углу Δφ в определенном масштабе, а направление совпадающее с осью вращения и определяемое правилом правого винта.

Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то έ совпадает по направлению с направлением ω в случае ускоренного вращательного движения и противоположна в случае замедленного вращения.

Связь между линейной и угловой скоростью и ускорением. О тдельные точки вращающегося тела имеют различные линейные скорости v , которые непрерывно изменяют свое направление и зависят от ω и расстояния r соответствующей точке до оси вращения.

Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ.

м обе части равенства на Δt:

, при Δt 0 получим пределы от левой и правой частей равенства:

Но

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. Известно, что

Откуда

И з написанных формул видно, что a_τ, a_n и a растут с увеличением расстояния точек до оси вращения. Формула v = ωr устанавливает связь между модулями векторов v, r, и ω, которые перпендикулярны друг к другу.

Т.к. ω | r ,то можно написать v = ω∙r∙sina это ничто иное как модуль векторного произведения. Таким образом v = [ ω r ] .

Рассмотренные простейшие виды движения твердого тела важны потому, что любое движение твердого тела сводится к ним.

Рассмотрим два последовательных положения тела А₁ и А₂. Из положения А₁ в положение А₂ тело можно перевести следующим образом: вначале А₁ в А¹ поступательно. Затем из положения А¹ в положение А₂ путем поворота на угол φ вокруг произвольной точки 0.

Следует отметить, что в вращательному движению применимы все формулы кинематики материальной точки с заменой в них линейных величин на соответствующие угловые.

Например: