Решение.

Для того чтобы по графику зависимости координаты тела от времени найти скорость тела в некоторый момент времени, необходимо определить тангенс угла наклона графика в соответствующей точке. Из графика видно, что на участке 1 координата бусинки не изменялась, а значит, бусинка покоилась. С другой стороны, на участке 2 координата бусинки изменялась со временем по линейному закону. Следовательно, на этапе 2 скорость бусинки была постоянна. Таким образом, верно утверждение 4.

Правильный ответ: 4.

Ответ: 4

2515

4

A 21 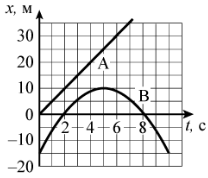 На рисунке приведены графики зависимости координат от времени для двух тел: А и В, движущихся по прямой, вдоль которой и направлена ось Oх. Выберите верное(-ые) утверждение(-я) о характере движения тел.

А. От момента t = 0 до остановки тело В проделало путь, равный 25 м.

Б. В момент времени, равный 2 с, тела А и В встретились.

1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б

Решение.

Тело В останавливается в момент времени , дальше оно начинает двигаться в противоположном направлении. За интервал времени от 0 с до 5 с тело В проделало путь, равный

 

.

Утверждение А верно.

Встречи двух тел соответствует пересечение графиков (в один и тот же момент времени, тела имеют одинаковую координату). Как видно из рисунка, графики не имеют точек пересечения, таким образом, тела А и В не встречались на протяжении рассматриваемого интервала времени. Утверждение Б не верно.

Правильный ответ: 1

Ответ: 1

4954

1

A 22 Массивный брусок движется поступательно по горизонтальной плоскости под действием постоянной силы, направленной под углом к горизонту. Модуль этой силы . Коэффициент трения между бруском и плоскостью . Модуль силы трения, действующей на брусок равен 2,8 Н. Чему равна масса бруска?

1) 1,4 кг 2) 2 кг 3) 2,4 кг 4) 2,6 кг

Решение.

Воспользуемся вторым законом Ньютона. Спроецируем все силы действующие на брусок на вертикальную ось. Брусок движется по горизонтальной плоскости, следовательно, у него нет вертикальной составляющей ускорения. Из второго закона Ньютона имеем:

,

где N — сила реакции опоры, а m — искомая масса. По условию, модуль силы трения равен

.

Отсюда, для массы бруска имеем:

.

Правильный ответ: 2.

Ответ: 2

703

2

A 22 Коэффициент трения резины колес автомобиля об асфальт равен 0,4. При скорости движения водитель, во избежание аварии, должен придерживаться радиуса поворота, не меньшего, чем:

1) 200 м 2) 100 м 3) 40 м 4) 10 м

Решение.

На повороте с радиусом R при скорости автомобиль имеет центростремительное ускорение . Это ускорение должна обеспечивать сила трения между колесами и дорожным покрытием, иначе начнется занос. В проекции на радиальную ось второй закон Ньютона приобретает вид: , где m — масса автомобиля. Для вертикальной оси имеем: , где N — сила реакции опоры. Принимая во внимание связь , реализующуюся как раз в случае минимального радиуса поворота, окончательно для минимального радиуса получаем

.

Правильный ответ: 2.

Ответ: 2

706

2

A 22 На рисунке представлена установка для исследования равноускоренного движения ползунка (1) массой 0,05 кг по наклонной плоскости, установленной под углом к горизонту.

 

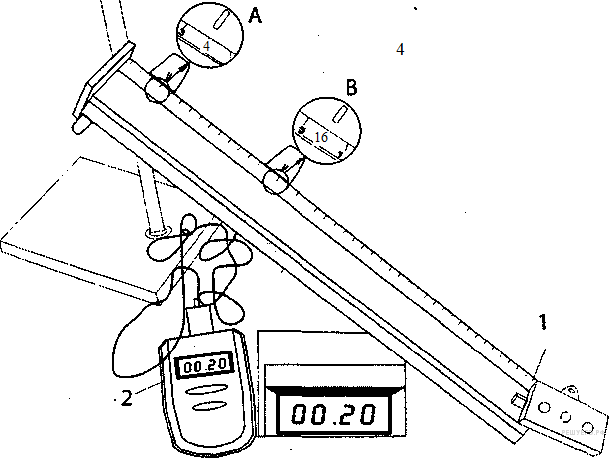
В момент начала движения верхний датчик (А) включает секундомер (2), при прохождении ползунка мимо нижнего датчика (В) секундомер выключается. Числа на линейке обозначают длину в сантиметрах. Секундомер измеряет время в секундах. Ускорение ползунка в любой момент времени вычисляется по формуле

1) 2) 3) 4)

Решение.

Поскольку ползунок начинает движение с нулевой начальной скоростью, путь, пройденный им к моменту времени t определяется выражением . Из рисунка видно, что за время он прошел . Отсюда находим, что ускорение равно

.

Оно остается постоянным на протяжении всего пути.

Правильный ответ: 1.

Ответ: 1

724

1

A 22 На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с. Определите скорость в начале торможения, если общий тормозной путь поезда составил 4 км, а торможение было равнозамедленным.

1) 20 м/с 2) 25 м/с 3) 40 м/с 4) 42 м/с

Решение.

Определим ускорение, с которым тормозил поезд. Рассмотрим последний километр. Начальная скорость на этом отрезке равна 10 м/с, конечная скорость — 0 м/с. Из формулы сразу находим модуль ускорения . Использовав эту же формулу, но теперь уже для всего отрезка торможения, находим начальную скорость: м/с.

Ответ: 1

3437

1

A 22 Шарик, закреплённый на лёгкой нерастяжимой нити длиной см, равномерно движется по окружности, лежащей в горизонтальной плоскости. При этом нить образует с вертикалью угол Определите модуль скорости шарика.

1) 12 м/с 2) 3,5 м/с 3) 3 м/с 4) 2,6 м/с

Решение.

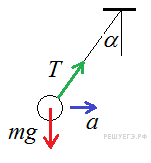Шарик двигается под действием двух сил: силы тяжести и силы натяжения нити . Они сообщают ему центростремительное ускорение , где  — радиус окружности, по которой вращается шарик. Выпишем второй закон Ньютона для шарика в проекции на вертикальную и горизонтальные оси: , .

Поделив одно уравнение на другое, для скорости имеем:

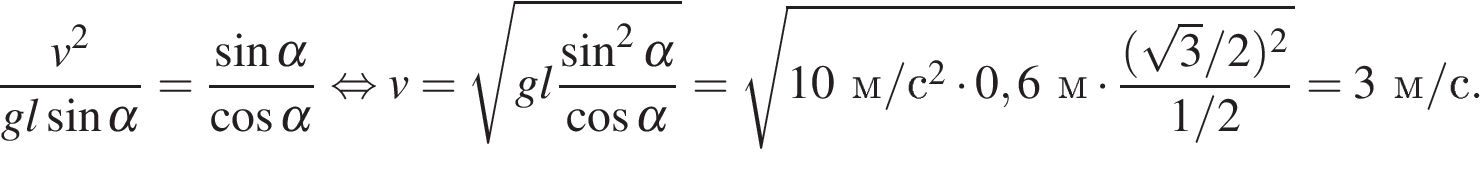
Правильный ответ: 3.

Ответ: 3

4098

3

A 22 Груз начинает свободно падать с некоторой высоты без начальной скорости. Пролетев 40 м, груз приобрёл скорость 20 м/с. На этом участке пути отношение изменения кинетической энергии груза к работе силы сопротивления воздуха равно

1) 1 2) −1 3) 2 4) 4