1.7. Структура плоских важільних механізмів

В основу структурного аналізу та синтезу механізмів покладено принцип, розроблений російським вченим Л.В.Ассуром (1878- 1920). Згідно з цим принципом будь-який плоский важільний механізм 3 кінематичними парами 1-го роду при його аналізі можна розділити на окремі прості частини - групи ланок. Кожна така група ланок утворює кінематичний ланцюг. Найпростіший кінематичний ланцюг, число ступенів вільності якого дорівнює числу ступенів вільності всього механізму, називається групою початкових ланок. Кінематичні ланцюги, число ступенів вільності яких дорівнює нулю, називаються групами з кульовим ступенем вільності або групами Ассура. Таким чином, будь який механізм можна вважати складеним із однієї групи початкових ланок і однієї чи кількох груп Ассура. Всі ці групи визначають структуру механізму, тому їх називають структурними групами.

До складу групи початкових ланок обов’язково входить нерухома ланка (стояк) і одна чи кілька початкових ланок. Число початкових ланок визначається числом ступенів вільності механізму. Якщо ступінь вільності механізму W= 1, то група початкових ланок має цілком визначений вигляд (рис,1.25) і складається із початкової ланки 1 та стояка 2, які утворюють або обертальну, або поступальну кінематичну пару. Якщо ступінь вільності механізму W= 2, то група початкових ланок складається із стояка і двох початкових ланок, які утворюють кінематичні пари із стояком (рис.1.25,а) або одна з одною (рис.1.25,б).

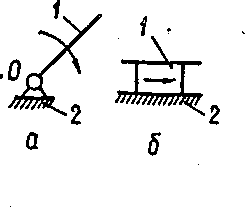
Рис. 1.25. Групи початкових ланок при а – початкова

ланка 1 утворює із стояком 2 обертальну кінематичну

пару; б – початкова ланка 1 утворює із стояком

2 поступальну кінематичну пару

Рис. 1.26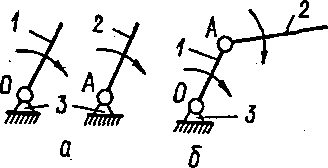 . Два варіанти групи початкових ланок при

W = 2: а – початкові ланки 1 і 2 утворюють кінематичні пари із стояком 3; б – початкові ланки 1 і 2 утворюють кінематичну пару одна з одною

Група Ассура являє собою кінематичний ланцюг, який після приєднання його вільними елементами до стояка має нульовий ступінь вільності і який не можна розділити на простіші кінематичні ланцюги, ступінь вільності яких також дорівнює нулю. До складу груп Ассура входять тільки рухомі ланки.

Нехай n' - число ланок в групі Ассура, - число кінематичних пар 1-го роду в групі Ассура, W'- ступінь вільності групи Ассура. Тоді із основної умови існування групи Ассура:

(1.3)

Рівність (1.3) можна задовольнити, якщо

,

де k - будь-яке ціле число ( К = 1,2,3,..., тощо).

Надаючи числу k різні значення, одержимо такі сполучення чисел ланок і кінематичних пар, що входять у групу Ассура:

k	1	2	3	……..
n'	2	4	6	……...
	3	6	9	………

При k = 1 маємо найпростішу групу Ассура, яка складається із двох ланок і трьох кінематичних пар. Ця група має п’ять видів залежно від кількості обертальних і поступальних пар та їхнього взаємного розташування (рис.1.27). Кінематична пара групи Ассура, за допомогою якої ланки з’єднані між собою, називається внутрішньою. Дві інші пари, якими група приєднується до сусідніх ланок механізму, називаються зовнішніми. Ланки групи, які входять до складу внутрішньої та зовнішньої кінематичних пар, називаються повідками. При k = 1 група Ассура має два повідки, а тому називається двоповідковою групою, або діадою. Кожний вид діади (рис.1.27) умовились позначати відповідним номером і назовати: діада N1, діада N2 тощо.

При k = 2 група Ассура складається із чотирьох ланок і вести кінематичних пар. На рис.1.28 наведено два варіанти групи Ассура при k = 2. Одна з них ( рис.1.28, а) називається триповідковою групою. Характерною ознакою другого варіанту групи (рмс.1.28,б ) є наявність замкнутого контуру. Якщо в цих групах Ассура одну або кілька обертальних кінематичних пар замінити поступальними парами, то можна одержати значну кількість різних

Рис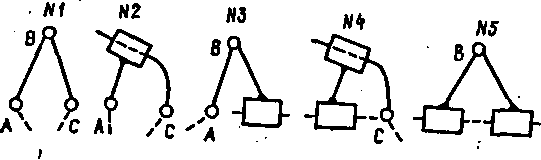 . 1.27. Види двоповідкової групи – діади (групи)

Асура 1-го классу: N1, N2, N3, N4, N5 – номери видів діад

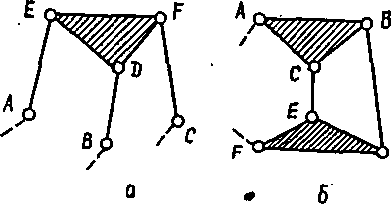
Рис. 1.28. Два варіанти групи Ассура 2-го класу: а-триповідкова група:

б-група із замкнутим контуром

видів груп Ассура при k = 2. Наприклад, тільки триповідкова група Ассура матиме 20 видів.

При k = 3 група Ассура мас шість ланок та дев’ять кінематичних пар і існує в десяти різних варіантах при наявності тіль­ки обертальних кінематичних пар.

Зазначимо, що у переважної більшості сучасних механізмів найчастіше зустрічаються двоповідкові групи Ассура (діади).

Всі групи Ассура за пропозиціє Г.Г.Баранова (1899-1960) ділять на класи залежно від числа k. При k = 1 група ланок називається групою Ассура 1 класу; при k = 2 - групою Ассура 2 класу тощо. Крім того, визначають також порядок групи Ассура (за І.І.Артоболевським) залежно від числа зовнішніх кінематичних пар, за допомогою яких група приєднується до інших ланок механізму. За вказаними ознаками всі діади (при k = 1) є групами Ассура 1 класу 2-го порядку. А зображені на рис.1.28 групи ланок при k=2 будуть групами Ассура 2 класу 3-го порядку (рис.1.28,а) та 2 класу 2-го порядку (рис.1.28,6,).

Розглянемо приклад структурного аналізу механізму повороту антени літакової радіолокаційної станції (рис.1.29}. У цьому механізмі n = 8, р₁ = 10, p₂ = 0, тоді число ступенів вільності

.

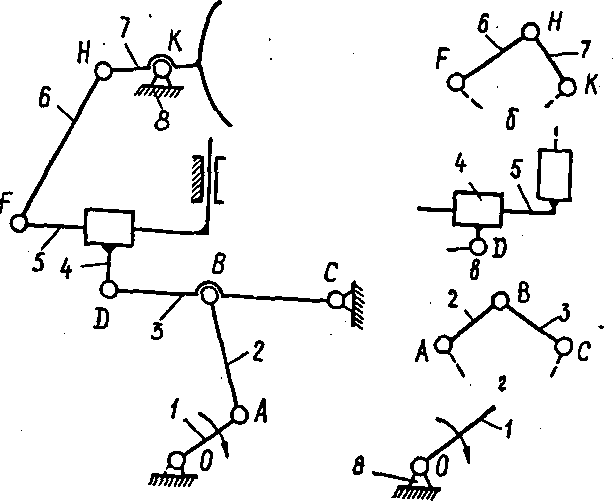
а д

Рис. 1.29. Визначення структури механізму повороту антени

літакової радіолокаційної станції: а – схема механізму; б – діада N1;

в – діада N4; г – діада N1; д – група початкових ланок

Отже, механізм має одну початкову ланку. За початкову вибираємо ланку 1, позначаючи її круговою стрілкою.

Визначити структуру механізму означав встановити з яких структурних груп ланок складається цей механізм та в якому порядку вони прнєднуються одна до другої.

Поділ механізму на структурні групи треба починати з групи Ассура, найвіддаленішої від початкової ланки. Починають із проби від’єднати від механізму найпростішу групу Ассура - діаду (n = 2,p₁ = 3). В нашому випадку це ланки 6 та 7 і обертальні кінематичні пари F , К , Н. Вони утворюють діаду N1 (рис.1.29, б). Частина механізму, яка залишилась, має також ступінь вільності W = 1 (n = 6; p₁= 7). Далі знову можна відділити діаду, яка складається із ланок 4 і 5 і трьох кінематичних пар: обертальної D і двох поступальних, одна з яких зовнішня, а друга - внутрішня. Ланки 4 та 5 утворюють діаду N4 (рис.1.29,в). Таким же чином відділяємо від механізму ланки 2 та 3 з обертальними кінематичними парами А, В, С, які утворюють діаду N1 (рис.І.29,г). Ланки 1 та 8, які утворюють обертальну кінематичну пару O, складають групу початкових ланок (рис.1.29.д).

Отже, запис структури механізму матиме такий вигляд:

ланки 6,7 - діада № І;

ланки 4,5 - діада № 4;

ланки 2,3 - діада № І;

ланки 1,13 - група початкових ланок.

Структурний аналіз в базою кінематичного та силового ана­лізу механізмів. В результаті структурного аналізу визначається ступінь вільності механізму, кількість, клас і вид структуріих груп, цо входять до його складу, та порядок їхнього приєднання до інших ланок механізму.

Ділення механізму на структурні групи дозволяє звести його кінематичне та силове дослідження до дослідження окремих груп ланок. Для структурних груп Ассура різних класів і видів розроблені спеціальні методи кінематичного та силового аналізу, які дозволюяють визначати положення, швидкості та прискорення окре­мих точок, а також зусилля в кінематичних парах будь-яких ва­жільних механізмів.