1.2. Класифікація кінематичних пар

Кінематичні пари класифікують за такими ознаками:

• за числом незалежних між собою можливих рухів однієї ланки відносно іншої, тобто за числом ступенів вільності у від­носному русі ланок, які утворюють кінематичну пару;

• за числом умов зв’язку, які накладаються кінематичною па­рою на відносний рух ланок, тобто за числом втрачених ланкою ру­хів при її входженні в кінематичну пару;

• за формою елементів ланок, що утворюють кінематичну пару.

За класифікацією В.В.Добровольского (1880-1957) залежно від числа можливих незалежних між собою рухів однієї ланки від­носно іншої кінематичні пари діляться на п’ять родів: 1-го роду (однорухомі), 2-го роду(дворухомі), 3-го роду (трирухомі), 4-го роду (чотирирухомі), 5-го роду (п’ятирухомі).

Таким чином, рід кінематичної пари визначається числом мож­ливих незалежних рухів однієї ланки відносно іншої, тобто числом ступенів вільності у відносному русі ланок.

З курсу теоретичної механіки відомо, що вільне абсолютно тверде тіло, що рухається у просторі, має шість ступенів віль­ності (рис.1.2). Таке тіло (ланка 1) може виконувати три оберталь­ні рухи навколо осей Х,Y,Z, та три поступальні рухи вздовж цих самих осей. Входження ланок у кінематичну пару накладає на їхній відносний рух певні умови зв’язку, тобто обмеження у русі однієї ланки відносно другої. Число таких умов зв'язку, тобто число втрачаємих ланкою рухів, може змінюватись у межах від 1 до 5. При цьому число можливих рухів ланки зменшується на відповідне число умов зв’язку і також може змінюватись у межах від 1 до 5. А тому і рід кінематичної пари змінюється в таких же межах.

Розглянемо приклади кінематичних пар. На рис.1.3 показана кінематична пара "куля-площина", Зона є парою 5-го роду, оскіль­ки куля (ланка 1) відносно площини (ланка 2) може виконувати п’ять незалежних рухів: три обертальні рухи навколо осей Х,Y, Z та два поступальні рухи вздовж осей X і Z

На рис.1.4 зображені кінематичні пари "циліндр-площина" (рис.І.4,а) та "куля-циліндр" (рис.І.4,б) . Вони є парами 4-го роду, оскільки в них ланка 1 відносно ланки 2 має чотири ступені вільності. В парі "циліндр-площина" ланка 1 (циліндр) відносно ланки 2 (площини) може обертатись навколо осей Y і Z та рва­тись поступально вздовж осей X і Z. .В парі "куля-циліндр" лан­ка 1 (куля) відносно ланки 2 (циліндра) може виконувати три обер­тальні рухи навколо осей Х,Y,Z та один поступальний рух вздопж всі Z.

Рис. 1.2 Можливі рухи вільної ланки у просторі

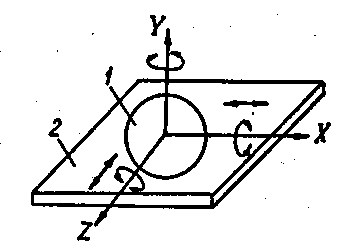
Рис. 1.3. Кінематична пара 5-го роду (куля - площина)

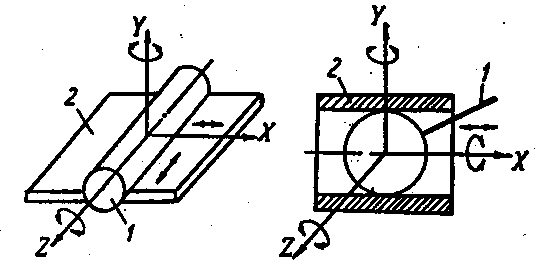
а б

Рис. 1.4. Кінематични пари 4-го роду:

а – циліндр – площина; б – куля – циліндр

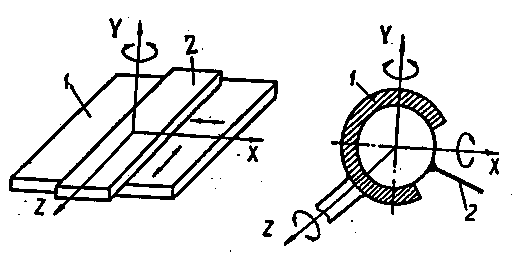
а б

Рис.1.5. Кінематичні пари 3-го роду:

а – площина; б – сферична

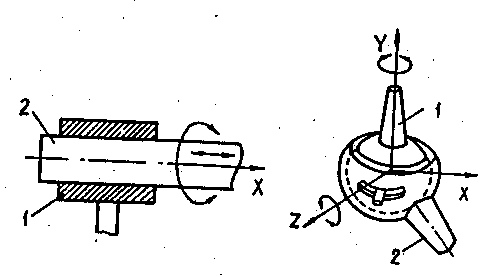
а б

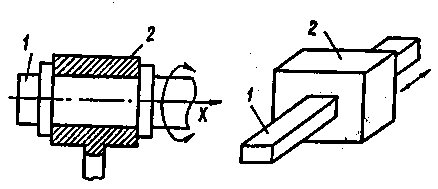
Рис. 1.6. Кінематичні пари 2-го роду:

а – циліндрична; б – сферична с пальцем

а б

Рис. 1.7. Кінематичні пари 1-го роду:

а – обертальна; б – поступальна

Приклали кінематичних пар 3-го роду показані на рис.1.5, 2-го роду - на рис.1.6. та 1-гo рoду на рис.1.7. Можливі рухи однієї ланки відносно-другої вказані стрілками.

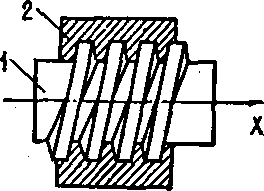
Слід зазначити, oо можливі рухи однієї ланки відносно дру­гої можуть бути або незалежними один від одного, або зв’язаними один з одним будь-якими додатковими геометричними умовами. На­приклад, у гвинтовій парі (рис.1.8) поворот гвинта (ланка 1) від­носно гайки (ланка 2), або, навпаки, ланки 2 відносно ланки І на певний кут викликає переміщання цієї самої ланки вздовж осі X на певну відстань. Але це переміщення ланки є залежним від кута 11 повороту. А числа ступенів кількості ланок кінематичної пари у їхньому відносному русі визначається числом можливих не­залежних рухів. Тому гвинтову пару слід віднести до пар 1-го ро­ду, бо е лише один параметр, що визначав положення гвинта в гайці (кут повороту ланки).

За класифікацією І.І.Артоболевського ( 1905- 1977 ) залежно від числа умов зв'язку, тобто числа обмежень, які накладаються кінема­тичною парою на відносний рух ла­нок, пари діляться на п'ять класів;

Рис.1.8. Гвинтова кінематична пара (1-го роду)

І, П, Ш, ІУ, У . Клас кінематич­ної пари визначається числом втрачених ланкою рухів при її входженні кінематичну пару.

Із визначення роду та класу кінематичних пар випливає, що кі­нематична пара 1-го роду за В.В.Добровольским є парою У класу за І І.Артоболевським; кінематична пара 2-го роду - парою ІУ класу тощо.

За класифікацією Ф.Рело (1829-1905 ) залежно від форми еле­ментів ланок кінематичні пари діляться на нижчі та вищі.

Нижчими називаються кінематичні пари, у яких ланки стика­ються між собою поверхнями (наприклад, обертальна, поступальна, гвинтова, циліндрична, сферична, сферична з пальцем, площинна).

Вищими називаються кінематичні пари, у яких ланки стикають­ся по лінії або в точці ( наприклад, куля-площина, циліндр-площина, куля-цилівдр).

Нижчі кінематичні пари можуть передавати більші зусилля, ніж вищі, завдяки більшій площі контакту міх ланками. Проте втра­ти на тертя у таких парах більші ніж у вищих. Наприклад, втрати на тертя у підшипниках ковзання значно більші, ній у підшипниках кочення.

Розглянуті кінематичні пари можуть бути утворені ланками про­сторових механізмів, тобто таких механізмів, точки ланок яких ру­хаються різних непаралельних площинах. У курсі "Теорія механіз­мів .І машин" будуть розглядатися переважно плоскі механізми, у яких точки всіх ланок рухаються паралельно одній нерухомій площині. У плоских-механізмах кінематичні пари можуть бути тільки 1-го та 2-го родів. Це пояснюється тим, що вільне тверде тіло у плос­кому русі мав тільки три ступені вільності: воно може рухатися поступально вздовж осей X і Z та обертатися навколо осі Y При входженні тіла (ланки) у кінематичну пару воно буде втрачати один або два стулені вільності. Тому кінематична пара буде одно- рухомо або дворухомою.

У плоских механізмах пари 1-го роду зпвкди никчі ( обертальні, поступальні, а пари 2-го роду - завжди вищі, причому можли­вими рухами однієї ланки відносно другої е поступальний та обер­тальний.

1.3. Умовні зображення кінематичних пар і ланок плоских механізмів

При структурному, кінематичному та динамічному дослідженнях механізми прийнято зображати у вигляді схем.

Схемою механізму називають Його графічне зображення, викона­не без масштабу за допомогою умовних позначень ланок та кінема­тичних пар.

Розрізняють також поняття кінематична схема механізму, на якій розміри ланок наводять у масштабі. На схемах механізмів лан­ки та кінематичні пари зображають умовно згідно з ГОСТ 2.770-68.

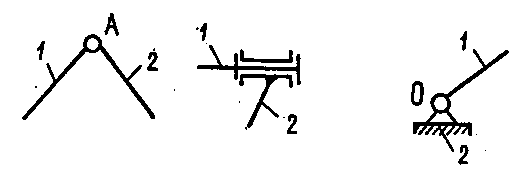
На рис.1.9 показані умовні зображення обертальної кінематичної пари. Центри обертальних пар позначаються великими літерами латинського алфавіту: А, В, С тощо. Ланки позначаються порядкови­ми арабськими цифрами: 1, 2, 3 тощо. Нерухомість ланки показують на схемах штриховкою.

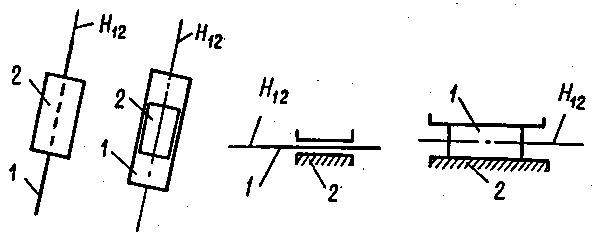
Умовне зображення поступальної кінематичної пари показано на рис.1.10. Напрямну поступальної пари позначають літерами Н з подвійним індексом у відповідності з номерами тих ланок, які утворюють кінематичну пару.

а б

Рис.1.9. Умовні зображення обертальної кінематичної пари:

а – ланки 1 і 2 – рухомі; б – ланка 2 – нерухома

а б

Рис.1.10. Умовні зображення поступальної кінематичної пари:

а – ланки 1 і 2 – рухомі; б – ланка 2 – нерухома

Умовні зображення. плоскої кінематичної пари 2-го роду наве­дені на рис.I .II. Рис а відповідає тому випадку, коли ланки яри роботі механізму послідовно отикаються одна одної всіма свої­ми точками (наприклад кулачок і ролик у кулачковому механізмі). ,.кцо ланки стикаються лише на деякій ділянці профілей (наприклад, зуб*я зубчестих коліс), то використовується аображення, показане на рис.1 11,б.

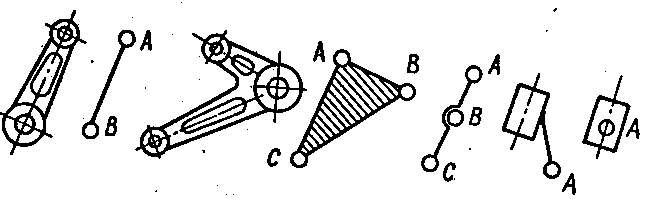
Приклади умовного зображення ланок плоских механізмів наве­дені на рис.1.12. Ланка, яка входить до складу двох чи трьох кінематичних пар, незалежно від конструктивної форми, зображається у вигляді прямої лінії або трикутника, який може заштриховуватися.

Назви та умовні зображення ланок залежно від їхнього харак­теру руху та конструктивної форми наведені у табл.1.1 Ці ланки

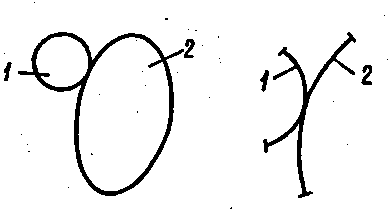
а б

Рис.1.11. Умовні зображення кінематичної пари 2-го роду:

а – ланки стикаються одна одної всіма точками профілей;

б – ланки стикаються на деякій ділянці профілей

а б в г

Рис.1.12. Умовні зображення ланки:

а – ланка входить у дві обертальні пари; б – ланка входить у три обертальні пари, які не лежать на одній прямій лінії; в – ланка входить у три обертальні пари, які лежать на одній прямій лінії; г – ланка входить до складу обертальної і поступально і кінематичних пар

називають: кривошипом - ланка важільного механізму, яка здійснює повний оберт навколо осі, зв'язаної із стояком; коромислом - ланка важільного механізму, яка здійснює неповний оберт навколо осі, зв'язаної із стояком; шатуном - ланка важільного механізму, яка здійснив плоскопаралельний рух; повзуном - ланка важільного механізму, яка здійсню поступальний рух відносно стояка або іншої ланки; кулісою - рухома ланка ванільного механізму, яка с напрямною для повзуна; кулачком - ланка з криволінійним профі­лем; зубчастим колесом - ланка із замкненою системою зуб’їв, яка

Таблиця 1.1

Основні типи ланок механізмів

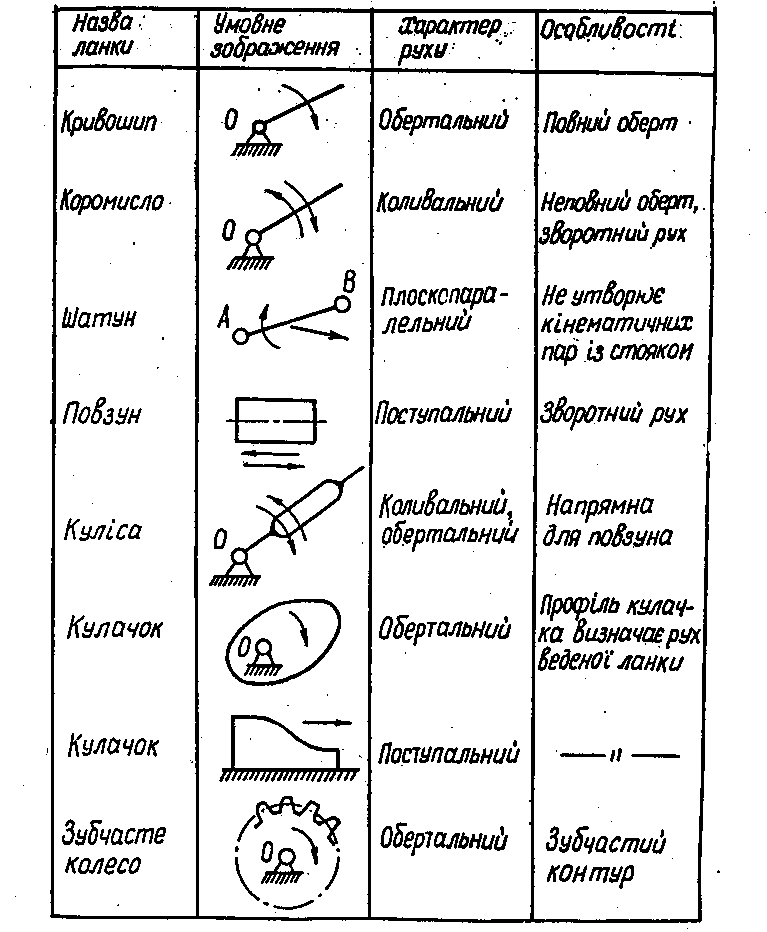
забезпечує за свій повний оберт безперервний рух парного зубчастого колеса.