2.5. Побудова планів швидкостей і прискорень механізму

Розглянемо декілька прикладів побудови планів швидкостей і прискорень механізму.

Кривошипно – повзунний механізм. Вважаємо заданими розміри ланок і закон руху кривошипа . Будуємо план механізму (рис.2.5., а) у вибраному масштабі і заданому кутом φ визначається за формулою (2.1):

.

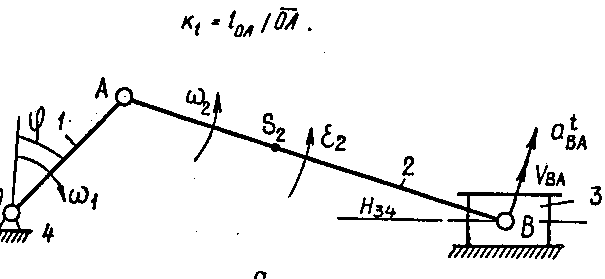
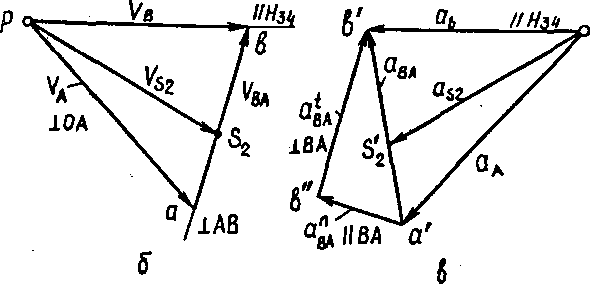
Рис.2.5. Побудова планів швидкостей і прискорень кривошипно – повзунного механізму: а – план механізму; б – план швидкостей; в – план прискорень

Знаючи кутову швидкість кривошипа ω₁ і його довжину , знаходимо швидкість точки А за формулою . Вектор напрямлений перпендикулярно до кровишипа ОА в бік його руху. Вибираємо довжину відрізка , який зображає на плані (рис.2.5.,б) швидкість точки А. Визначамо масштабний коефіцієнт швидкостей

.

Поршень (ланка 3), а, отже, і точка В, яка належить ланці 3 здійснює поступальний рух вздовж напрямної Н₃₄. Одночасно точка В, як і точка А, належить ланці 2 (шатуну). Для визначення швидкості точки В напишемо векторне рівняння

,

де , .

Тут і в подальшому вектор, відомий за значенням і напрямком, будемо підкреслювати двома лініями, а вектор, відомий тільки за напрямком – однією лінією.

Векторне рівняння має визначене рішення, якщо в ньому лише два невідомі елемента. Такими невідомими елементами в останньому рівнянні є значення швидкостей V_B і V_BA. Для визначення цих невідомих елементів у відповідності з векторним рівнянням проводимо через точку а (рис.2.5,б) лінію, яка показує напрямок відносної швидкості , а з полюса р – лінію, яка паралельна напрямку руху повзуна (ǁН₃₄). Точка перетину цих ліній визначає точку b – кінець векторів і . Відрізок визначає швидкість V_B, а відрізок - швидкість V_BA. Знаходимо величини цих швидкостей з формул

та .

Відрізок є планом швидкостей шатуна АВ. А тому точка S₂ яка лежить на ньому, на плані швидкостей, згідно з теоремою подібності, буде лежати на відрізку . Склавши пропорцію

,

Знаходимо довжину відрізка

.