2.4. Теореми подібності для швидкостей та прискорень

При кінематичному дослідженні механізмів часто користуються простим геометричним методом визначення швидкості та прискорену будь-якої точки ланки, якщо знайдені швидкості та прискорення двох інших точок цієї ланки.

Теорема подібності для Швидкостей. Нехай швидкості точок А, В * С деякої ланки (рис.2.4,а) відомі за величиною і напрямом. Зобразимо ці швидкості відрізками ра ,рЬ ,рс , відклавши їх ві однієї точки р (рис.2.4,б). З’єднаємо прямими лініями кінці веторів цих швидкостей (точки а _, Ь , с) . Відрізок ав зображав швидкість точки В відносно точки А (тобто швидкість Vba) відрізок ВС відносну ШВИДКІСТЬ Vcb відрізок ca. - відносну швидкість Vac . Таке графічне зображення називається планом швидкостей ланки, а точка р - полюсом плана швидкостей.

У зв'язку з тим, що всі точки належать очній ланці, швид­кість V ba перпендикулярна прямій АВ на плані ланки, швидкість Vcb┴BC і швидкість Vac ┴ СА. Тaким чином, всі сторони трикутни­ка abc перпендикулярні відповідним сторонам трикутнина АВС . От же, ці трикутники подібні. Звідси одержуємо теорему подібності для швидкостей: прямі лінії, які з’єднують точки на плані ланки, і прямі лініі, які з'єднують кінці векторів швидкостей цих точок на плані швидкостей, утворюють подібні фігури. Фігура на плані швидкостей повернута відносно фігури на плані ланки на 90°.

У подібних фігурах всі відповідні сторони пропорційні. Тому згідно теореми подібності можна написати

Теорема подібності дозволяє знаходити швидкість будь-якої точки ланки, якщо відомі швидкості двох інших точок цієї ланки. Нехай, наприклад, відомі швидкості точок А і В . Знайдемо швидкість точки С . Для цього через точку а (рис.2.4, б) проводимо пряму лінію перпендикулярно АС ,а через точку B - лінію перпендикулярно BС. У перетині цих ліній знаходимо точку с. Відрізок рс зображає швидкість точки С.

Рис.2.4. Визначання швидкостей і прискорень точок однієї ланки:

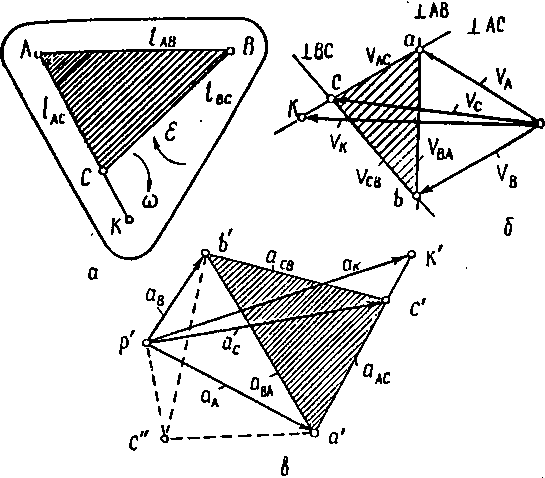
а – план ланки; б – план швидкостей; в – план прискорень

Якщо треба визначити також швидкість точки К , що лежить на прямій АС , то спочатку із пропорції знаходимо відрізок

а потім, відкладаємо цей відрізок від точки С по лінії аС (рис.2.4,б). Таким чином знаходимо положення точки К і, отже, швидкість Vk . При цьому точки а ,c,k на плані швидкостей повинні бути розташовані у тій же послідовності, що і точки ЛСта А на плані ланки (рис.2.4,а).

Теорема подібності для прискорень. Нехай повні прискорення точок А,В і С зображені на плані прискорень ланки(рис.2.4, а) відрізками , які відкладені від точки р' – полюса плана прискорень. З’єднаємо точки а', b' і с' прямими лініями. Відрізки виражають відності прискорення точки В відносно точки А, точки С відносно точки В і точки А відносно точки С. Ці прискорення можна визначити за відомими з теоретичної механіки формули

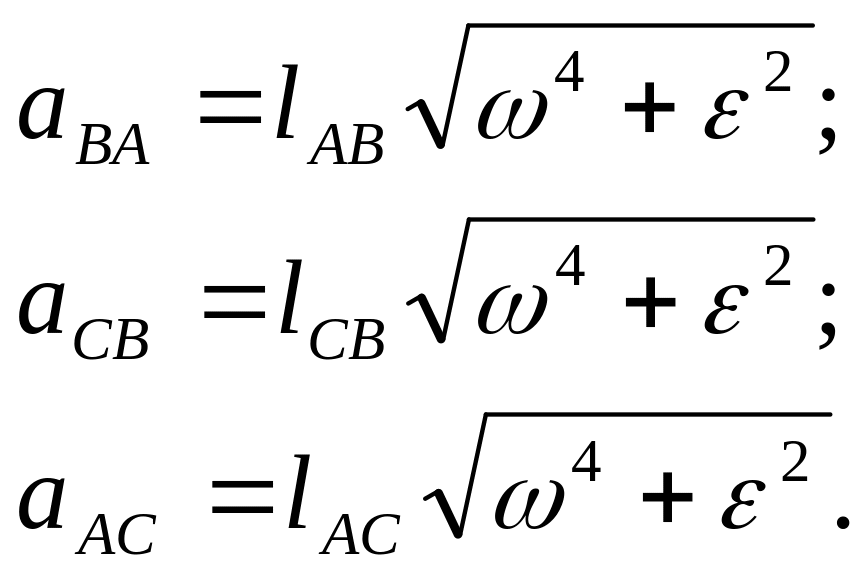
Із цих рівнянь одержимо

або 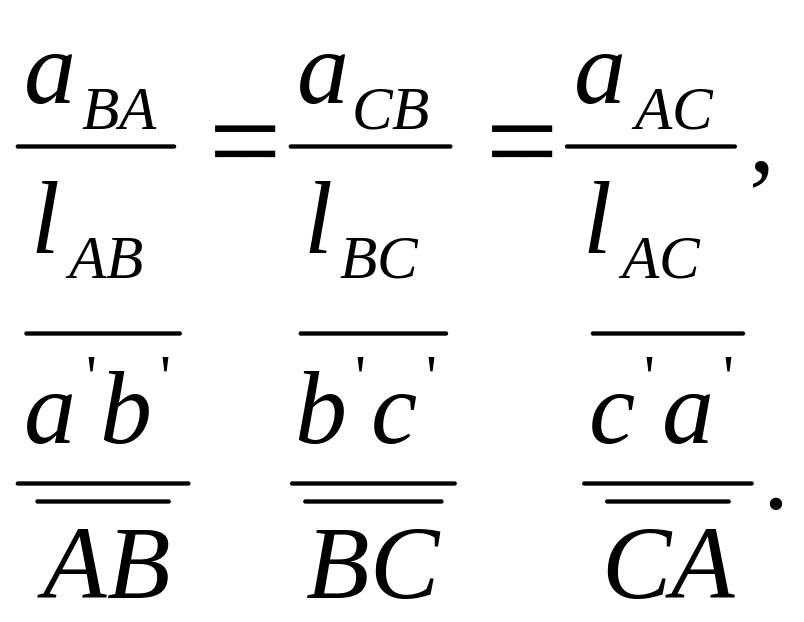(2.5)

З одержаних рівностей випливає, що у трикутників a'b'c' і АВС відповідні сторони пропорційні. Отже, ці трикутники подібні. Звідси одержуємо теорему подібності для прскорень: прямі лінії, які з’єднують точки на плані ланки, і прямі лінії, які з’єднують кінці векторів повних прискорень цих точок на плані прискорень, утворюють подібні фігури.

Користуючись теоремою подібності, визначимо прискорення точки С, якщо відомі прискорення точки А і В. Для цього із пропорції (2.5) знаходимо відрізки

та

і цими відрізками, як радіусами, описуємо кола навколо точок a' і b'. Проведені кола перетнуться в точках С' і С''. Вірною є та точка, яка відповідає правилу обходу контурів. Обійдемо контур (трикутник) АВС (рис.2.4.,а), рухаючись від точки А до точки В а потім до точки С і повертаючись до точки А. Як бачимо, обхід контуру відбувається за годинниковою стрілкою.

При обході контуру (трикутника) a'b'c' (рис.2.4.,в) рух відбувається також за годинникової стрілкою, а при обході контуру a'b'c' проти годинникової стрілки. Тому вірним є положення точки С'.

Якщо треба визначити також повне прискорення точки К, що лежить на прямій АС, то спочатку знаходимо із пропорції відрізок

,

потім відкладаємо цей відрізок від точки С' по лінії a'c' (рис.2.4.,в), зберігаючи порядок розташування точок а', с', k' та точок A, C, K. Відрізок зображає повне прискорення точки К.