5. Приклади побудови нейромережевих систем керування динамічними об'єктами

1. Нейромережева модель системи керування ГТД

Будемо думати, що за результатами спостереження в реальних умовах польоту за функціонуванням авіаційного двувального газотурбінного двигуна (ГТД) потрібно побудувати нелінійну динамічну модель САК ГТД на основі рекурентної НМ. У якості вихідних даних використовуються оцифровані показання бортового самописа (пристрою реєстрації даних), що відповідають деякій ділянці польоту (рис. 5.4.21) тривалістю T = 5 хв 20 с.

При періоді дискретизації, рівному T₀ = 1 c, це означає, що навчальна вибірка містить 320 крапок (часових відліків). Необхідна точність побудови моделі – не гірше (3...4) % в усьому діапазоні часу спостереження. Помітимо, що всі наведені на рис. 5.4.21 змінні є відносними (безрозмірними) і отримані шляхом розподілу вихідних фізичних параметрів ГТД на їх максимальні (гранично можливі) значення. т.т. належать інтервалу [0, 1].

Для рішення завдання ідентифікації за допомогою НМ (див. рис. 5.4.15, а) скористаємося розглянутим у розд. 5.4.6 методом «часового вікна». Відповідно до цього методу, на вхід НМ послідовно подаються L дискретних відліків сигналу u(k -L),u( k - L+1),..., u(k -1), що перебувають у межах часового вікна. У нашім випадку, під входом u(k) розуміється значення сигналу α_ВУД(k), тобто задавального впливу на вході САК в k-й, момент часу (t = kT₀). У якості бажані значень виходів НМ розглядаються значення виходів об'єкта y_і, (і = 1,2,..., m) у моменти часу k - L+1, k - L+2, ..., k. У розглянутому прикладі – це значення вихідних параметрів двигуна T_T^*, n₁ і n₂. Таким чином, таблиця, у якій зберігається L «четвірок» – дані навчальної вибірки НМ у межах зазначеного часового вікна, приймає наступний вид (табл. 5.4.1).

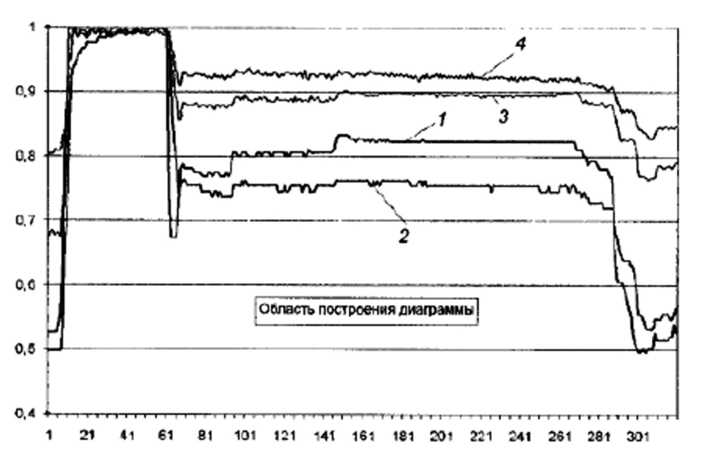
Рис. 5.4.21. Графіки зміни контрольованих параметрів ГТД:

1 – положення важеля управління двигуном ВУД (α_ВУД); 2 – температура загальмованого потоку газів за турбіною T_T^*; 3 – частота обертання ротора компресора низького тиску п₁; 4 – частота обертання ротора компресора високого тиску п₂

Таблиця 5.4.1.

Навчальна вибірка
Час	αВУД	TT*	п1	п2
k - L	………...
k - L + 1		………….	…………..	…………..
…	…	…
к

Вхід НМ Виходи НМ

Базова структура нейромережевої моделі системи, побудованої на основі рекурентної мережі Елмана, представлена на рис. 5.4.22. Тут вхідний шар НМ складається з (σ + 1) нейронів, на входи яких подаються значення сигналів α_ВУД (k) і із затриманих (на один такт) виходів нейронів схованого шару х_i(k + 1),..., х_σ(k + 1); виходами НМ є значення спостережуваних параметрів двигуна T_T^*, п₁, п₂ в (k + 1) -й момент часу.

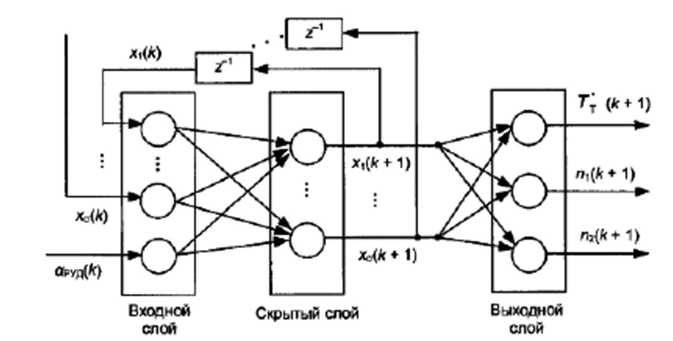
Рис. 5.4.22. Структура нейромережевої моделі