5. Синтез структури багаторежимного нейромережевого регулятора

Як відзначається багатьма авторами, задача вибору структури й параметрів нейромережевого регулятора в замкнутій системі керування динамічним об'єктом залишається багато в чому відкритою. Це пов'язане з нелінійністю характеристик об'єкта керування, необхідністю обліку декількох режимів роботи САК, неоднозначністю завдання вимог до якості процесів керування.

Розглянемо далі формалізовану постановку задачі синтезу нейромережевого регулятора (НМ-регулятора) на основі критерію мінімальної складності, при виконанні заданих вимог до точності, стійкості і якості перехідних процесів на фіксованій множині режимів роботи об'єкта.

Будемо думати, що метою синтезу є вибір:

• типу (архітектури) використовуваної НМ;

• місця включення НМ у САК;

• необхідної складності НМ-регулятора;

• складу навчальної вибірки;

• алгоритму навчання НМ-регулятора.

Постановка задачі синтезу. Вимоги до структури синтезованого НМ- регулятора. Допустимо, що динаміка об'єкта керування (ОК) описується диференціальним рівнянням «вхід - вихід», заданим у неявному виді:

φ(y⁽ⁿ⁾, y^(n-1), …, y; u^(m), u^(m-1), …, u) = 0, (5.4.13)

де u = u(t) і y = y(t) – вхід і вихід досліджуваного об'єкта відповідно; т і n – максимальні порядки похідних u⁽ⁱ⁾ , y^(j) для вхідної й вихідний змінних u(t) і (m ≤ n), φ(•) – деяка нелінійна функція.

Для простоти передбачається, що об'єкт є одномірним (багатомірний випадок розглядається нижче), керованим і спостережуваним.

Потрібно побудувати такий регулятор (у класі нейромережевих структур), що забезпечував би керування об'єктом (5.4.13) при дотриманні наступних вимог до синтезованої системи автоматичного керування:

• астатизм (нульова статична помилка);

• фізична реалізуємість НМ-регулятора;

• стійкість і задана якість процесів керування на фіксованій множині М ={M₁,…, M_R} режимів роботи об'єкта;

• мінімальна складність НМ-регулятора.

Зупинимося докладніше на цих вимогах.

Астатизм. Дана вимога забезпечується шляхом включення інтегруючої ланки (інтегратора) до складу системи керування. Можливі варіанти побудови структурної схеми САК зображені на рис. 5.4.19. а-в.

Найбільш простий варіант побудови дискретного інтегратора для реалізації операції чисельного інтегрування в дискретному часі k = 1,2...., описується різницевим рівнянням:

v(k) = v(k-1)+T₀e(k-1) (5.4.14)

або дискретною передатною функцією:

(5.4.15)

де ; Т₀ - період дискретизації.

Фізична реалізуємість. Будемо думати, що в якості НМ на рис. 5.4.19.а-в приймається рекурентна нейронна мережа на базі 3-шарового персептрона. структура якого зображена на рис. 5.4.20.

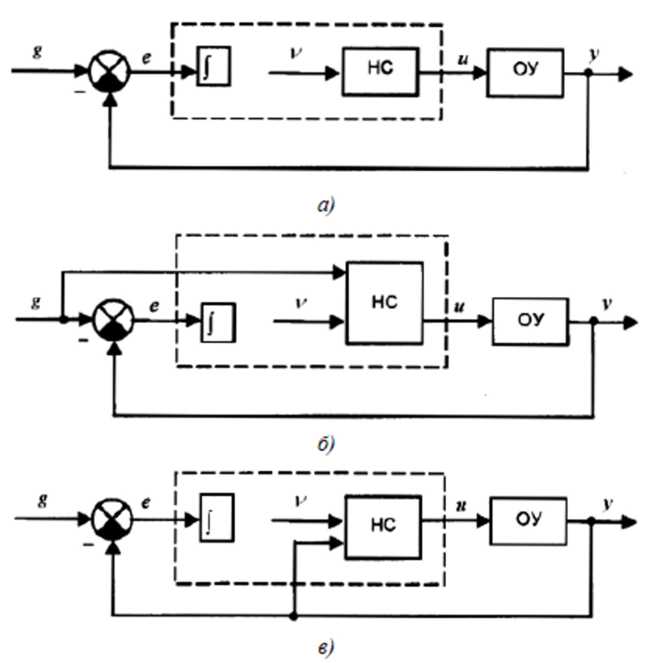
Рис. 5.4.19. Схема астатичних САК з НМ-регуляторами

Досліджуваний НМ-регулятор містить у собі (р + q + 1) нейронів у вхідному шарі, що здійснюють перерозподіл сигналів, що поступають на їх входи між нейронами наступного шару, а також σ нейронів у схованому шарі й один нейрон у вихідному шарі, зв'язок між якими здійснюються за допомогою налаштованої ваги W_αβ, (навченої),

W_β, (α =1,2,…, p + q + 1; β = 1,2,…, σ)

Динаміка даної мережі описується різницевим рівнянням

u(k) = F( u(k – 1),…, u (k – q), v(k),…, v(k – p)), (5.4.16)

де F(•) – нелінійна функція відносно зазначених (р + q + 1) аргументів, конкретний вид якої залежить як від обраних активаційних функцій нейронів, так й від значень ваги синоптичних зв'язків W_αβ, W_β. У якості активаційної функція нейрона може бути прийнята, наприклад, раціональна сигмоїда виду y = х /(c + | х |), де c > 0.

Як видно з рис. 5.4.20. вихідний сигнал НМ u(k) у поточний момент часу k залежить як від поточного значення вхідного сигналу v(k), так і від минулих значень вхідного й вихідного сигналів, затриманих на відповідне число тактів (періодів дискретизації). Таким чином побудова НМ на основі структури, наведеної на рис. 5.4.20, не пов'язана з необхідністю використання майбутніх (що не з'явилися) значень вхідного сигналу, що гарантує фізичну реалізуємість регулятора. В принципі, співвідношення між максимальним числом тактів затримки по входу р і виходу q в (5.4.16) може бути довільним. В окремому випадку, при відсутності елементів часової затримки (р = 0, q = 0), маємо з (5.4.16): u(k) = F(v(k)), що відповідає структурній реалізації звичайного (статичного) персептрона.

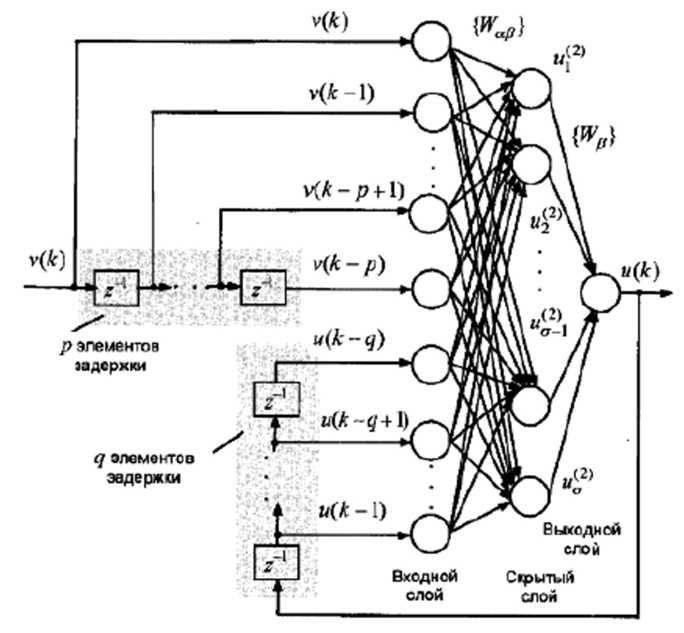
Рис. 5.4.20. Структура рекурентної НМ

Помітимо, що змінні v(k) й u(k) на схемі вважаються нормованими, тобто вони належать інтервалу [-1, 1], що передбачає використання операції масштабування, пов'язаної з переходом від фізичних координат (входу й виходу регулятора) до їх відносних безрозмірних значень.

Стійкість і задана якість процесів керування. Допустимо, що задано деяку множину базових режимів роботи об'єкта керування (ОК), координати, що характеризуються набором, М_r ⁼ (u₀^(r), y₀^(r)) (r = 1,2,..., R), де u₀^(r), y₀^(r) – фіксовані (сталі) значення входу й виходу об'єкта для r-го базового режиму: R – число таких режимів. Як видно із рис. 5.4.19, для того щоб підтримувати задане значення y = y₀^(r) на виході об'єкта, досить подати постійний, задавальний вплив (уставку) g₀^(r) на вхід САК. Необхідною умовою працездатності САК є стійкість замкнутої системи керування на кожному із зазначених базових режимів роботи об'єкта. (Помітимо, що виконання даної вимоги не є тривіальним, оскільки розглянута система є нелінійної й стійкість кожного режиму повинна досліджуватися окремо).