Застосування нейронних мереж у задачах ідентифікації динамічних об'єктів
Нагадаємо, що під ідентифікацією розуміється одержання математичного опису (моделі) об'єкта за результатами спостережень за його вхідними й вихідними змінними в процесі функціонування. Метою ідентифікації є спроба відтворити (змоделювати) реальні характеристики об'єкта керування й виробити в остаточному підсумку правильну стратегію керування об'єктом. Розглянемо можливі підходи до рішення задачі ідентифікації за допомогою НМ, приділивши основну увагу проблемі ідентифікації нелінійних динамічних об'єктів.
Один з таких підходів заснований на так званій нелінійній моделі ковзного середнього (Nonlinear Moving - Average Model). Ідея побудови даної моделі заснована на розкладанні нелінійного функціонала, що описує поводження об'єкта, у ряд Вольтера в дискретні моменти часу:
(5.4.10)
де λ0, λi, λij, – невідомі параметри.
Для апроксимації 1-х членів ряду (5.4.10) можна використовувати зображену на рис. 5.4.17 структуру рекурентної НМ, де символ z-1 позначає елемент затримки на один такт (Т0).
Модель у цьому випадку описується рівнянням:
ŷ(k + 1) = F(u(k), u(k – 1),…, u(k – P)); (5.4.11)
де число Р вибирається виходячи з необхідної точності наближення ряду.
В окремому випадку, коли функція F є лінійною, формула (5.4.11) визначає середньозважене значення відліків вхідного сигналу за (Р + 1) попередніх тактів: звідси – зазначена назва моделі. Навчання НМ зводиться до вибору таких її параметрів, при яких помилка між виходами об'єкта й мережі мінімальна.
Інший можливий підхід заснований на поданні рівнянь динамічного об'єкта в просторі станів, тобто моделі «вхід - стан - вихід». Перш ніж розглянути відповідні рівняння нелінійного об'єкта, нагадаємо, що аналогічна модель для лінійного дискретного об'єкта в просторі станів має вигляд
X(k+1) = AX(k) + BU(k), Y(k) = СХ(k), (5.4.12)
де U (k), Y(k) і X(k) – вектори входу, виходу й стану об'єкта розмірністю l, m ,n; А, В,C – матриці числових коефіцієнтів розміру n x n; n x l; m x n – відповідно.
Графічне подання моделі (5.4.12) показане на рис. 5.4.18. а., де I - одинична матриця розміру n x n.
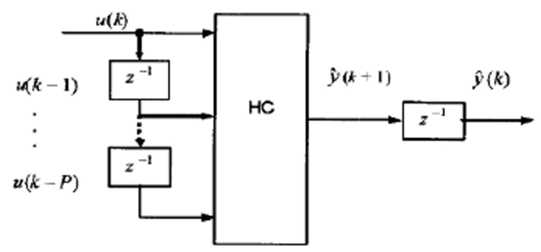
Рис. 5.4.17. Модель сковзного середнього
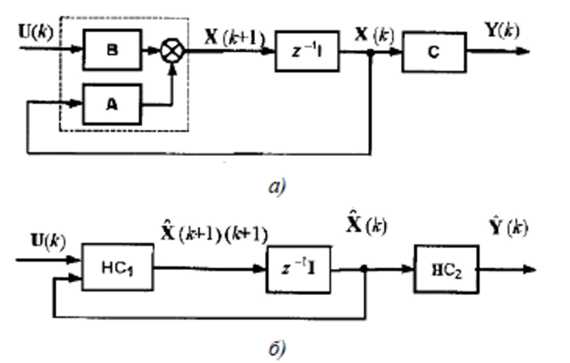
Рис. 5.4.18. Моделі об'єкта в просторі станів
У загальному випадку, рівняння нелінійного динамічного об'єкта можуть бути записані як:
X(k + 1) = F(X(k)),U(k), Y(k) = Н(Х(k)), (5.4.33)
де F і H – невідомі матричні функції (оператори). Тоді реалізацію даної моделі за допомогою НМ можна представити у вигляді схеми, показаної на рис. 5.4.18. б, де нейронні мережі HМ1 і НМ2 використовуються відповідно для апроксимації операторів FH: Ẋ(k) і Ỹ (k) – оцінки вектора стану й виходу об'єкта.
При навчанні HМ1 і НМ2, загалом кажучи, можливі два варіанти. У першому з них, коли вектор стану об'єкта Х(k) доступний виміру, параметри обох мереж можуть налаштовуватися автономно, з умови мінімізації помилок Е(k) = Ẋ(k) -X(k) і Δ(k) = Ỹ(k) -Y(k) відповідно. У другому випадку, коли вектор стану Х(к) не виміряється, процедура навчання HМ1 і НМ2 помітно ускладнюється через неможливість безпосереднього використання алгоритму зворотного поширення.
Ще одна можливість – застосування НМ для побудови нелінійної моделі «вхід - вихід». Для одномірного об'єкта керування, що має один вхід і один вихід (SISO, Single Input - Single Output), подібна залежність визначається рівнянням:
ŷ(k + 1) = F(ŷ (k), ŷ (k – 1),…, ŷ (k – q), u(k), u(k),…, u(k – p)) (5.4.34)
і може бути реалізована за допомогою рекурентної НМ, схема якої представлена на рис. 5.4.12. Конкретний вид апроксимуючої функції F(•) установлюється в результаті налаштування ваги НМ із умови забезпечення мінімуму помилки ε(t) = ŷ(t) - y(t), тобто різниці між виходами нейронної мережі й об'єкта. Перевага даної схеми – менші обчислювальні витрати за рахунок застосування алгоритму зворотного поширення.
Важлива й дуже перспективна область застосування нейромережевих моделей – їх використання як моделей для прогнозування (предикторів). У цій якості вони усе ширше використовуються для прогнозу стану складних динамічних об'єктів, прийняття оперативних управлінських рішень і т.д.