5. Нечіткі нейронні мережі

Порівнюючи описані вище нейромережеві алгоритми з розглянутими в 3-й главі алгоритмами, заснованими на нечіткій логіці, легко бачити, що кожний із цих підходів має свої переваги й недоліки. Нейронні мережі легко навчаються на прикладах, вилучаючи при цьому знання з «сирих» даних, однак цей процес найчастіше є тривалим і можливе «зависання» у локальних мінімумах функції помилки. Крім того, знання, отримані в результаті навчання НМ, «розмазані» по всіх нейронах у вигляді значень вагових коефіцієнтів (тобто навчена мережа – це завжди «чорний ящик» для користувача).

Нечіткі алгоритми, навпроти, зрозумілі й зручні для пояснення одержуваних з їх допомогою висновків. Разом з тим процес формалізації знань у вигляді продукцій до кінця не автоматизований і пов'язаний з певною непередбаченістю. Звідси виникає природний інтерес до застосування гібридних технологій у формі нечітких нейронних мереж (Fuzzy Neural Networks), у яких висновки робляться на основі апарата нечіткої логіки, а відповідні функції приналежності нечітких множин налаштовуються з використанням алгоритмів навчання нейронних мереж.

Нечіткі нейронні (гібридні) мережі є яскравим представником нової галузі обчислювального інтелекту – м'яких обчислень. Термін «м'які обчислення» (Soft Computing) був уперше уведений в 1994 р, «батьком нечіткої логіки» Л. Заде. Згідно Л. Заде, м'які обчислення – це об'єднання методологій обчислень, що базуються на нечіткій логіці, нейронних мережах, генетичних алгоритмах і імовірнісних обчисленнях. Пізніше в цей конгломерат були включені міркування на базі свідчень (Evidential Reasoning), мережі довіри (Belief Networks), хаотичні системи й розділи теорії машинного навчання. У порівнянні із традиційними, «твердими» обчисленнями, м'які обчислення більш пристосовані до всеосяжної неточності реального миру Керівним принципом м'яких обчислень є «терпимість до неточності, невизначеності й часткової істинності для досягнення зручності маніпулювання, робастності, низкою вартісттю рішення й кращого узгодження з реальністю».

У м'яких обчисленнях важливо те, що складові їх методології доповнюють один одного й забезпечують синергетичний ефект, а не конкурують один з одним. Таким чином, спільне використання перерахованих вище технологій дозволяє в багатьох випадках одержати більш високу якість рішення завдання, чим застосування їх окремо, що дозволяє говорити про ключову роль м'яких обчислень у створенні й розвитку інтелектуальних систем керування й прийняття рішень.

5. Загальні принципи побудови нейромережевих систем керування динамічними об'єктами

Як уже відзначалося в розділі 5.4.1, НМ починають відігравати помітну роль при створенні систем автоматичного керування (САК) складними динамічними об'єктами. До таких об'єктів належать сучасні літальні апарати, силові й енергетичні установки. мобільні роботи й ін. Для них характерні відсутність точних математичних моделей або їх надмірна складність, висока розмірність простору станів й прийнятих рішень по керуванню, ієрархічність, різноманіття критеріїв якості, високий рівень шумів і зовнішніх збурень.

На рис. 5.4.14 показані області найбільш ефективного застосування сучасних технологій керування. Як видно з рисунка, класичні методи керування добре працюють при повністю детермінованому об'єкті керування й детермінованому зовнішньому середовищі. Для систем з неповною інформацією й високою складністю об'єкта керування оптимальними є нечіткі й нейромережеві САК, причому в найбільш складних випадках доцільним виявляється застосування нейромережевих систем керування.

Відомий спеціаліст в області теорії керування професор Єльського університету (США) К.С. Нарендра пропонує умовно розділити труднощі, що виникають при побудові САК складними динамічними об'єктами, на три основні категорії:

1. обчислювальні складності;

2. наявність нелінійності;

3. невизначеність.

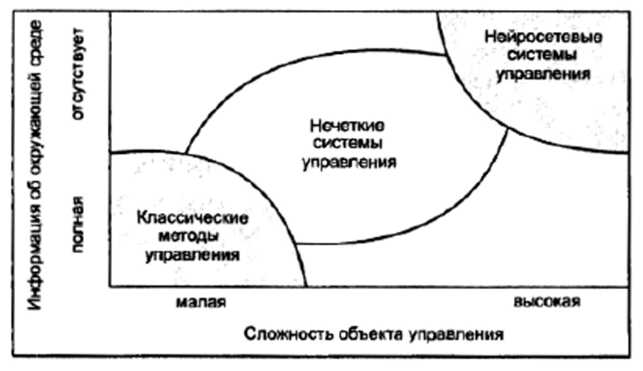
Рис. 5.4.14. Області застосування різних технології керування

Як показують численні дослідження, НМ успішно справляються з усіма трьома категоріями згаданих труднощів. Спочатку паралельна природа цих мереж забезпечує обчислення з високими швидкостями. Мережі, що містять нелінійні компоненти, можуть бути використані для апроксимації нелінійних відображень із будь-яким бажаним ступенем точності. Та обставина, що параметри НМ можуть налаштовуватися в реальному часі з обліком вхідних вихідних даних, указує на те, що вони можуть використовуватися в складі інтелектуальних систем керування, забезпечуючи високу якість функціонування цих систем в умовах істотної невизначеності (недостатності) інформації про об'єкт керування й зовнішнє середовище.

Існують різні способи застосування НМ у системах керування. Так, нейронна мережа може використовуватися для одержання нелінійної математичної моделі y = F(u) об'єкта (процесу) керування по вхідним вихідним даним, тобто для рішення задачі ідентифікації (рис. 5.4.15. а). При цьому порівнюються вихід об'єкта y(t) і вихід нейронної мережі ŷ(t) при тому самому вхідному впливі u(t), а процедура навчання НМ складається в зміні ваги її зв'язків таким чином, щоб зменшити неузгодженість ε(t) = y(t) - ŷ(t) до прийнятної (досить малої) величини.

Інший варіант використання НМ - одержання інверсної (зворотної) математичної моделі об'єкта керування (рис. 5.4.15, б). Тут на вхід нейронної мережі подається вихід об'єкта керування y(t), а під бажаною реакцією НМ розуміється вхід об'єкта u(t).

Таким чином, мінімізуючи величину помилки ε(t) = ŷ(t) - u(t) у процесі навчання НМ, одержуємо в підсумку ŷ (t) ≈ u(t), тобто навчена нейронна мережа відтворює нелінійну функціональну залежність u = F^-1(y) – інверсну модель об'єкта. Даний тип моделей використовується, наприклад, у завданнях керування роботами-маніпуляторами, коли потрібно визначити бажаний закон зміни керуючого впливу u = u(t), що забезпечує зміну вектора керованих координат об'єкта Y(t) у відповідності заданою програмою Y = Y_npoг(t).

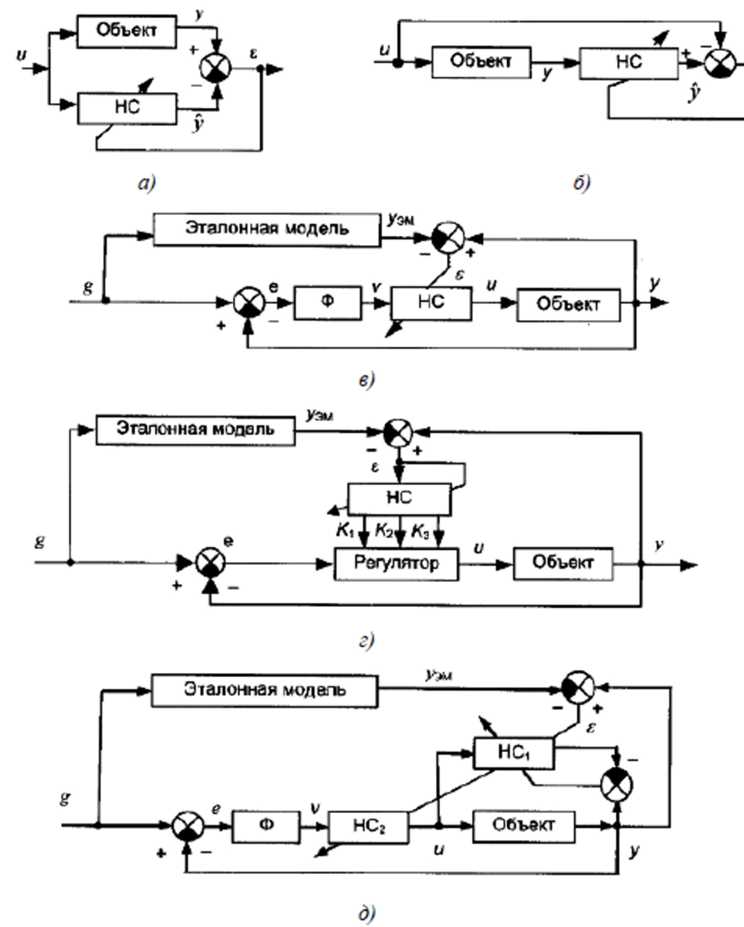
Рис. 5.4.15. Структурна схема САК з використанням НМ

Можливе безпосереднє включення НМ як регулятор у замкнутий контур керування об'єктом (рис. 5.4.15, в). При цьому на вхід нейронної мережі подається сигнал помилки керування з виходу фільтра керування Ф, вихід мережі u(t), одночасно є входом об'єкта; ціль навчання НМ – зменшити величину неузгодженості ε(t) = y(t) - у_ем(t) між виходами об'єкта й еталонної моделі системи. Вибираючи відповідним чином оператори еталонної моделі й фільтра Ф, вдається забезпечити бажану динаміку САК в широкому діапазоні зміни параметрів об'єкта.

Інший варіант використання НМ – її застосування як блок налаштування параметрів основного (лінійного) регулятора (рис. 5.4.15, г). Допустимо, що рівняння динаміки цього регулятора має вигляд:

(5.4.9)

де К₁, К₂, К₃, – коефіцієнти підсилення пропорційної, інтегральної й диференціальної складової відповідно (тобто як лінійний регулятор використовується ПІД-регулятор). Тоді навчання нейронної мережі зводиться до формування такого вектора параметрів К = (К₁, К₂, К₃), при якому забезпечується мінімальна неузгодженість ε(t) = y(t) - у_ем(t).

Загальна процедура синтезу інтелектуальних САК з використанням НМ наведена на рис. 5.4.16.

Зупинимося коротко на кожному з етапів зазначеної процедури.

1. Як видно з рис. 5.4.16. приступаючи до синтезу, розробник повинен мати відповіді на наступні питання.

Для яких цілей створюється система?

Що собою представляє об'єкт керування?

Які завдання ставляться перед системою?

Які засоби є в розпорядженні розробника для рішення зазначених завдань?

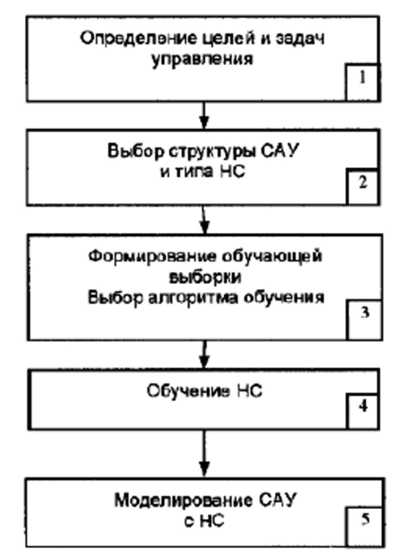
Рис. 5.4.16. Процедура проектування нейромережевої САК

Відповіді на поставлені питання, як правило, знаходяться у технічному завданні (ТЗ) на проектування САК й містять у собі:

• ціль даної розробки;

• позначення конкретного об'єкта керування;

• режими його роботи й умови функціонування;

• основні функції проектованої системи керування;

• вимоги до показників якості САК.

Крім того, передбачається, що розробник має достатній обсяг професійних знань у даній предметній області, має інформацію про близькі по призначенню й технічним параметрам САК (прототипах), а також про результати експериментальних досліджень і математичного моделювання об'єкта.

2. Наступний етап проектування пов'язаний з вибором структури (конфігурації) системи й типу НМ, для досягнення поставлених перед САК цілей. Критерієм вибору структури САК є принцип мінімальної складності: серед всіх можливих алгоритмів керування, заданих вимог, що забезпечують виконання, вибрати найпростіший. Тому варто підкреслити, що використання НМ у САК виявляється виправданим лише в тих випадках, коли застосування традиційних (більш простих) алгоритмів не дає бажаного результату, тобто спроектована система виявляється непрацездатною в силу значної складності (нелінійність, невизначеність, розкид параметрів) об'єкта керування.

Далі виникають наступні питання: «Яка архітектура НМ є в цьому випадку найбільш кращою? Як вибрати необхідну структуру НМ, т.т., кількість вхідних нейронів і кількість зв'язків між ними, у рамках даної архітектури?».

Читач, що ознайомився з матеріалом попередніх розділів 5.4. 3-5.4.5, уже має уявлення про такі архітектури НМ, як:

• багатошарові персептрони;

• радіально-базисні мережі;

• мережі Хопфілда:

• мережі Кохонена;

• рекурентні нейронні мережі;

• нечіткі нейронні мережі.

Безумовно, такий (далеко не повний) перелік способів побудови НМ дає багаті можливості з погляду досягнення цілей, що ставляться перед САК, з урахуванням специфіки об'єкта керування й умов його функціонування. Так, персептрони й РБФ-мережі дозволяють побудувати практично будь-яке нелінійне відображення, тому що є універсальними апроксиматорами. Нечіткі НМ являють собою нейромережеву реалізацію алгоритмів нечіткого керування. Мережі Хопфілда й Кохонена незамінні при рішенні завдань розпізнавання образів (ситуацій) і оптимізації. Рекурентні НМ успішно використовуються при ідентифікації динамічних об'єктів, побудові динамічних регуляторів, прогнозуванні часових рядів.

При виборі структури НМ необхідно виходити з того, що її складність повинна відповідати складності завдання керування (згадаємо вже згадуваний принцип «необхідної розмаїтості» Ешбі). На практиці складність завдання керування звичайно визначається обсягом (розмірністю) навчальної вибірки.

Загальна процедура структурного синтезу нейромережевого регулятора мінімальної складності буде розглянута в розділі 5.4.8.

3. Процес формування навчальної вибірки використовуваної для навчання НМ у складі САК, має свої особливості.