4. Інші архітектури нейронних мереж

Як показує аналіз літератури, персептрони є найбільш поширеними, однак далеко не єдиним способом побудови НМ. На сьогодні відомо більше 200 різновидів (архітектури) НМ, що істотно розрізняються по своїх властивостях, алгоритмам навчання, спектру розв'язуваних завдань. Розглянемо коротко деякі з них.

1. Радіально-базисні мережі

Даний клас мереж, називаних РБФ-мережами (RBFN, Radial Basis Functions Networks), належить до багатошарових НМ прямого поширення й був уперше запропонований в 1988 р. Д. Брумхедом і Д. Лове. Пізніше було доведено, що ці мережі також є універсальними апрксиматорами тобто з їх допомогою можна як завгодно точно апроксимувати будь-яку безперервну функцію декількох змінних.

Архітектура РБФ-мережі включає у себе три шари нейронів. Перший (вхідний) шар виконує розподільні функції. Другий (схований) шар здійснює фіксоване нелінійне перетворення вектора входів X = (х₁,х₂,...,х_n)^T у новий простір U = (и_1,и₂,...,u_р)^T без використання вагових коефіцієнтів, що набудовуються. Вихідний шар поєднує отримані в такий спосіб виходи нейронів схованого шару шляхом обчислення їх лінійної вагової комбінації (рис. 5.4.6).

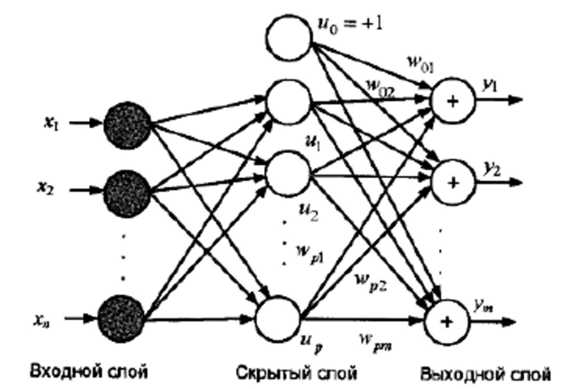
Рис. 5.4.6. Структура РБФ-мережі

Виходи мережі описуються рівняннями

де X = (х₁,х₂,...,х_n)^T – вхідний вектор; w_li – ваги зв'язків. (l = 1,2,...,р, i = 1,2,...,m); w_0i – зсув по i-му виходу мережі. Функції f (X) – це функції активації нейронів схованого шару, визначені як

f_l(X)=φ_l(||X-C_l||), (l=1,2,…,p),

де (||X-C_l||) – норма вектора X-C_l = (x₁ - С_l2, х₂ - C_l2,..., x_n- C_ln)^Т; C₁ = (С_l1,.C_l2,...,С_ln)^Т l-й вектор-еталон, що задається в якості «центра» l-й області вхідних образів: φ_l(•) - радіальна базисна функція (φ_l ≥ 0), що приймає максимальне значення при нульовому значенні аргументу й швидко убуває при (||X-C_l||) → ∞. Це має на увазі, що значення функції φ_l(•) тільки тоді істотно відрізняються від нуля, коли вхідний вектор X близький до вектора С_l.

Функції f_l (X) можуть бути обрані, наприклад, в класі гаусових функцій

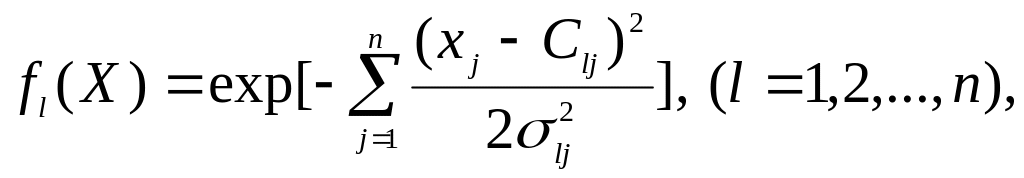(5.4.4)

де ϭ_lj, - параметр, що визначає «ширину» гаусовії функції.

Вид функції f для l-го нейрона прихованого шару показано на рис. 5.4.7.

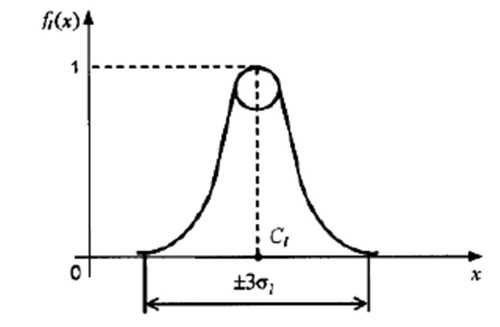
Рис. 5.4.7. Функція активації нейрона прихованого шару

Оскільки параметри мережі, що налаштовуються лінійно пов'язані з виходами у_i, то вони можуть бути знайдені безпосередньо за допомогою методу найменших квадратів. При цьому мінімізується сумарна квадратична помилка мережі

(5.4.5)

де y^r_j – j-й вихід НМ у r-му експерименті, тобто при пред'явленні мережі r-го вхідного образа X^r; d^r_j – бажаний j-й вихід мережі для входу X^r; R – число експериментів (розмірність навчальної вибірки). Обчислюючи часні похідні

і прирівнявши їх до нуля з урахуванням виразів

приходимо до системи з (р + 1)т – лінійних рівнянь відносно (р + 1)т невідомих коефіцієнтів w_0j, w_1j,...,w_pj, .(j = 1,2,....т).

На відміну від ситуації коли використання градієнтних методів при настроюванні ваги персептрона приводить лише до досягнення локальних мінімумів, тут знаходження ваги зв'язків здійснюється швидше й точніше. Цьому сприяє й та обставина, що якщо вхідний вектор Х^r приймає значення, близькі до центрів навчання С_l то реакція цієї радіальної базисної функції φ_l (•) велика: та навпаки, реакція приблизно дорівнює нулю, коли вхід Х^r далекий від С_l. Це також позначається на підвищенні швидкості навчання мережі.

Як показують експерименти, при малому числі входів (n≤3) радіально-базисні мережі мають очевидні переваги над багатошаровими нейронними мережами, забезпечуючи високу точність апроксимації будь-якої безперервної вектор-функції Y = F(X). Це робить їх привабливими для рішення завдань ідентифікації й керування. У той же час для більших значень n число необхідних базисних функцій різко зростає. При цьому необхідно ретельно вибирати розташування центрів С_l базисних функцій, що вимагає знання апріорної інформації про величину (рівні) вхідних сигналів.

2. Нейронні мережі Хопфілда

Мережа Хопфілда була запропонована в 1982 р. американським біофізиком, професором Каліфорнійського технологічного інституту Джоном Хопфілдом. Дана мережа являє собою динамічну систему, побудовану на основі одношарової не здатної до навчання НМ зі зворотними зв'язками (рис. 5.4.8). Кожний компонент u_i вхідного вектора U подається тут на відповідний (i-й) нейрон, тобто число нейронів дорівнює числу входів (і числу виходів) мережі. Всі нейрони зв'язані один з одним зваженими зв'язками причому вага цих зв'язків w_ij фіксована. Кожний вихід мережі y_i являє собою затримане значення виходу відповідного нейрона; z^-1 – оператор часового зсуву на один такт.

Поводження мережі Хопфілда в часі описується системою різницевих рівнянь

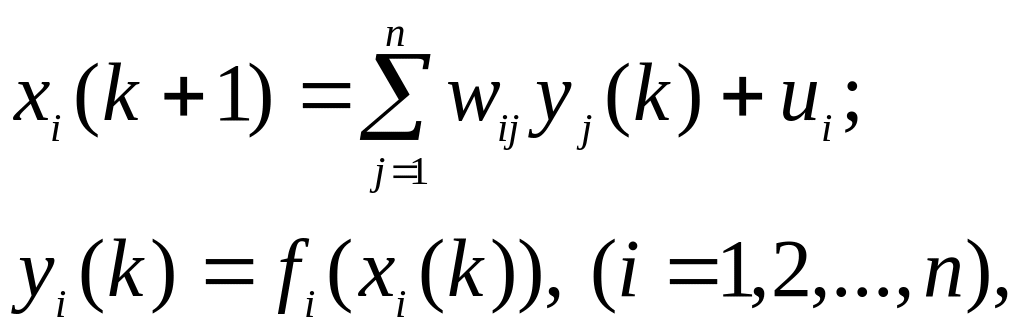(5.4.0)

де х_і – сумарне порушення (змінна стану) і-го нейрона; f_i (•) – функція активації нейрона; к- дискретний час.

Достатні умови збіжності мережі Хопфілда до стійкого стану:

Стан мережі визначає в кожний момент часу деяку крапку у фазовому просторі. Оскільки відповідно до рівняння (5.4.6) сигнал з виходу кожного нейрона подається на входи всіх інших, то стан мережі починає змінюватися до тих пір. поки мережа не прийде в один з найближчих стійких станів. При цьому всі нейрони на кожному наступному кроці будуть виробляти той же сигнал, що й на попередньому.

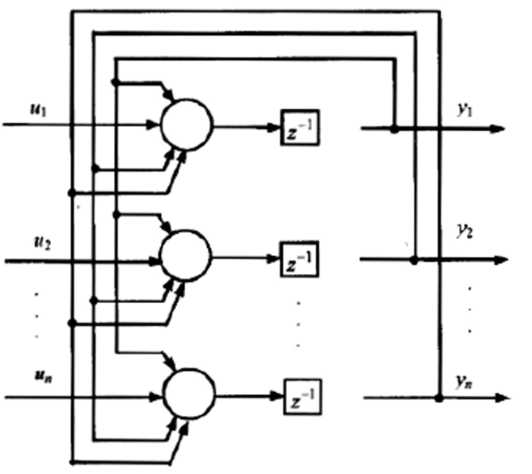
Рис. 5.4.8. Структура мережі Хопфілда

Достатні умови збіжності мережі Хопфілда до стійкого стану:

а) симетричність матриці ваги синоптичних зв'язків (w_ij = w_ji), тобто матриця ваги зв'язків W = (w_ij)_nxn повинна рівнятися своїй транспонованій матриці: W = W^T;

б) всі елементи головної діагоналі матриці W повинні бути нульовими (w_ii = 0 для всіх i = 1,2,...,n).

В окремому випадку, коли f_i(•) є граничною функцією, виходи нейронів u_і, приймають значення 0 або 1. При цьому стійкий стан мережі відповідає однієї з вершин n - вимірного гіперкуба (на рис. 5.4.9 показані можливі стійкі стани бінарної мережі Хопфілда для п = 2 і п = 3).

Рис. 5.4.9. Стани мережі Хопфілда

Конкретне влучення зображучої крапки фазового простору в одну із зазначених вершин залежить від значень синоптичної ваги w_ij а також від входів мережі u_i, що визначають початкові стани нейронів. Сказане можна інтерпретувати в такий спосіб: вибір ваги синоптичних зв'язків (що. загалом кажучи, представляє самостійне завдання) визначає «пам'ять» НМ. т.т., сукупність запам’ятованих образів, кожний з яких зв'язується з деяким стійким станом мережі. Якщо вхідний образ (тобто вектор U) частково неправильний або неповний, то мережа із сукупності запам’ятованих образів вибирає прототип, найбільш схожий на пропонований образ.

Область застосування мереж Хопфілда – розпізнавання образів (у тому числі відновлення повної інформації із фрагментів), побудова асоціативної пам'яті рішення різних завдань оптимізації комбінаторного типу (приклад – широко відома в математиці завдання про комівояжера).

3. Нейронні мережі Кохонена

Дана архітектура була запропонована в 1982 р. професором Хельсінкського технологічного університету (Фінляндія) Тейво Кохоненом. Мережа належить до класу нейронних мереж, що самоорганізовуються, (Self-Organizing Maps), що використовує алгоритми навчання без учителя для налаштування ваги синоптичних зв'язків.

Ідея побудови такої мережі, представленої на рис. 5.4.10. полягає в наступному. Нейронна мережа складається із двох шарів. Перший (вхідний) шар здійснює розподіл вхідних сигналів х₁,х₂,...,х_n між нейронами другого шару, називаного шаром (картою) Кохонена. Нейрони 2-го шару розташовуються на площині й зв'язані між собою зв'язками, сила яких залежить від відстані між нейронами й має звичайно вид «мексиканського капелюха» (рис. 5.4.11).

Подібний характер зв'язків забезпечує взаємне посилення сигналу близькими нейронами й ослаблення впливу далеких нейронів, внаслідок чого порушення якого-небудь нейрона приводить до утворення деякої області із сусідніх збуджених нейронів, що має досить яскраво виражені границі.

Навчання нейронної мережі здійснюється шляхом почергового пред'явлення їй вхідних образів X¹ ,Х² ,...,X^R з наступним налаштуванням ваги зв'язків нейронів 2-го шару, що виробляється з урахуванням відстані між нейронами 2-го шару:

Тут W_ij – ваговий вектор нейрона з координатами (i,j); h(p,t,k) – функція притягання р- го й t-го нейронів; γ = 1/2,(k = 1,2,...); || – норма відповідного вектора.

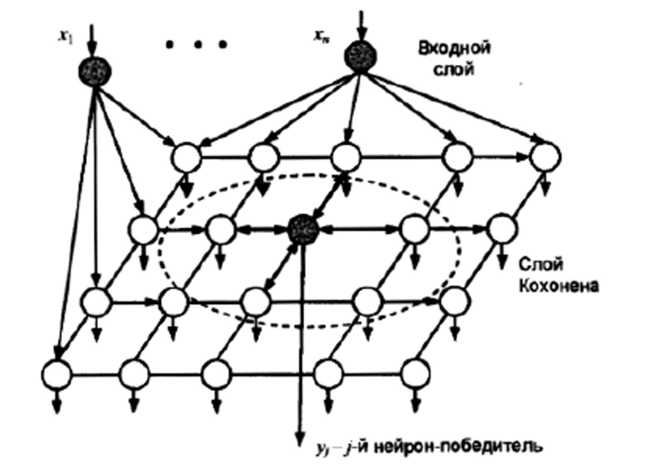
Рис. 5.4.10. Структура нейронної мережі Кохонена

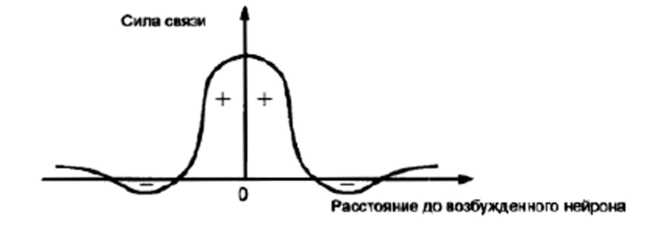
Рис. 5.4.11. Характер взаємозв'язків між нейронами

У результаті навчання виявляється такий нейрон шару Кохонена, який при подачі на вхідний шар деякого образа (вектора) Х^r виявляється збудженим більше інших (нейрон – «переможець»). Даний нейрон є найбільш близьким до пропонованого образа, оскільки вихід кожного нейрона 2-го шару визначається як сума зважених входів мережі.

У своєму найпростішому виді мережа Кохонена діє за принципом «Переможець забирає все». Це означає, що для даного вхідного вектора Х^r тільки один нейрон 2-го шару видає на виході логічну 1. всі інші видають 0. У випадку, коли нейронній мережі пред'являють різні образи, нейрони розбиваються на підмножини, кожна з яких «відгукується» на образи цілком певного типу (тобто «схожі» образи), отже, мережа має навички класифікації (кластеризації) пред'явлених їй образів.

Мережі Кохонена набули широкого застосування в задачах розпізнавання образів, оптимізації й керування.

4. Рекурентні нейронні мережі

Під рекурентними нейронними мережами розуміються НМ, що мають одну або кілька зворотних зв'язків. Вище вже розглядався один зі способів побудови таких мереж - одношарові повнозв’язані мережі Хопфілда (див. рис. 5.4.8). Інший важливий клас рекурентних (динамічних) НМ, що набувли широке застосування в задачах керування, – рекурентні нейронні мережі на базі багатошарового персептрона (RMLP Recurrent Multi - Layer Perceptron).

Уперше найбільш повно подібні мережі були описані у фундаментальних джерелах, де вони були названі нейронними мережами з часовими затримками (TD NN, Time Delay Neural Networks). Структура узагальненої рекурентної НМ, що має р елементів затримки для вхідного сигналу u(k) і q елементів затримки для вихідного сигналу y(k). наведена на рис. 5.4.12. Значення u(к) і y(к) у кожний момент часу k тут є скалярними величинами, тобто розглядається одномірний випадок.

Рис. 5.4.12. Структура рекурентної нейронної мережі

Таким чином, вектор вхідних сигналів персептрона містить у собі наступні компоненти:

• поточне й попереднє значення входу мережі u(k), u(k – 1), …,u(k – p);

• значення вихідного сигналу u(k), u(k – 1), …,u(k – q +1) у попередні моменти часу.

Динаміка мережі, зображеної на рис. 5.4.12, описується нелінійним різницевим рівнянням

y(k + 1) = F(y(k),..., y( k – q + 1), u(k),…, u(k – p); (5.4.7)

де конкретний вид функції F є результатом виконання деякої процедури навчання НМ. Розглянута мережа являє собою, по суті нелінійний адаптивний фільтр із кінцевою пам'яттю (тобто рекурсивний фільтр).

В окремому випадку, при відсутності зворотних зв'язків з виходу НМ одержуємо із рівняння (5.4.7):

y(k + 1) = F(u(k), u(k – 1),…, u(k – p)); (5.4.8)

що відповідає подачі на вході персептрона в кожний (k-й) момент часу «вікна» з (p + 1) часових відліків u(k), u(k – 1), …,u(k – p), сформованих за допомогою p елементів затримки. Дана схема відповідає адаптивному нерекурсивному фільтру й одержала широке поширення в задачах прогнозування часових рядів.

Інший можливий варіант побудови рекурентної НМ був запропонований в 1990 р. Дж. Елманом. У мережі Елмана зворотні зв'язки подаються на входи мережі з виходів нейронів схованого шару. Структура такої мережі для багатомірного випадку, коли U(k) і Y(k + l) - вектори входів НМ розмірністю l й т відповідно, зображена на рис. 5.4.13.

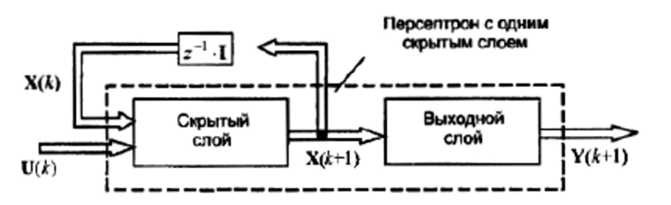
Рис. 5.4.13. Рекурентна мережа Елмана

Тут Х(k) – вектор змінних стану НМ, тобто виходів нейронів схованого шару (розмірності п) у момент часу k, I - одинична матриця розмірності пхп. Таким чином схований шар НМ складається з п нейронів, на входи яких подаються значення компонентів вхідного вектора u₁(k), u₂(k),...u_l(k), а також затримані на один такт значення виходів цих нейронів x₁(k), x₂(k),...x_n(k),

Рівняння динаміки мережі Елмана приймають вид

X(k + l) = F_l(X(k),U(k);

Y(k) = F₂(X(k)), (5.4.25)

де F₁ і F₂ – нелінійні вектор-функції (оператори), що визначають необхідну відповідність «вхід - вихід» нейронної мережі.

Рекурентні мережі отримали широке застосування при рішенні завдань ідентифікації, прогнозування й керування нелінійні динамічні об’єктами. У якості функції активації нейронів при їх побудові звичайно використовується сигмоїдна функція або гіперболічний тангенс. Найпоширеніші алгоритми навчання – алгоритм зворотного поширення і його модифікації (див. розділ 5.4.3).

Більш докладно інформацію про характеристики розглянутих вище НМ, особливостях їх практичного застосування, а також про інші, не менш цікаві способи побудови нейронних мереж (НМ адаптивного резонансу, рециркуляційні мережі, мережі зустрічного поширення, мережі Хеммінга, автоасоциативні НМ й ін.) можна знайти у загальній літературі російською мовою: в области теории нейронных сетей.