3. Багатошарові персептрони

1. Структура нейронної мережі, алгоритми навчання

До числа найбільш популярної архітектури НМ належать так звані мережі прямого поширення (тобто без зворотних зв'язків) – багатошарові персептрони.

Загальна схема побудови багатошарового персептрона показана на рис. 5.4.3. де кружками позначені елементарні перетворювачі інформації - нейрони, а стрілками - зв'язки між цими нейронами, що мають різну «силу» (вага синоптичних зв'язків).

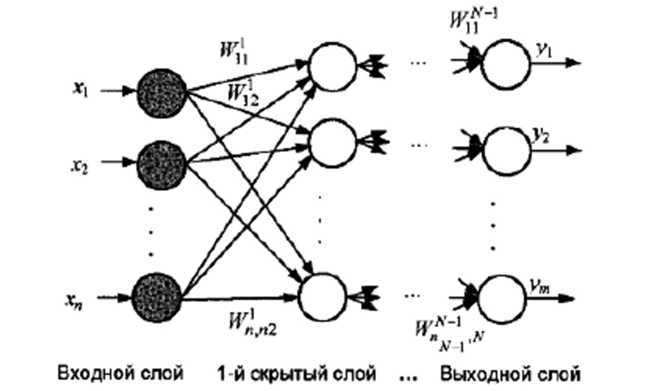
Рис. 5.4.3. Структурна схема багатошарового персептрона

Як видно з рисунка, багатошаровий персептрон складається з декількох шарів нейронів: вхідного шару; одного або більше схованих, або проміжних, шарів (називаних так у силу того, що вони «не видні» користувачеві) й вихідного шару нейронів. Вхідний вектор X = (x_l, x₂,... x_n)^T подається на вхідний шар, а вихідний вектор Y = (y_l, y₂,... y_m)^T визначається шляхом почергового обчислення рівнів активності елементів кожного шару (від 1-го схованого шару до вихідного) з використанням уже відомих реакцій елементів попередніх шарів.

Відмінні риси персептрона:

• нейрони кожного шару не зв'язані між собою;

• вхідний сигнал кожного нейрона надходить на входи всіх нейронів наступного шару;

• нейрони вхідного шару не здійснюють перетворення вхідних сигналів, їх функція полягає тільки в розподілі цих сигналів між нейронами 1-го схованого шару.

5.4.3.2. Завдання апроксимації функції

Важлива обставина, що визначає підвищений інтерес до використання багатошарових персептронів у задачах інтелектуального керування, полягає в їх здатності апроксимувати із заданою погрішністю будь-яку безперервну нелінійну функцію, внаслідок чого ці мережі часто називають «універсальними апроксиматорами».

Доказ даного твердження базується на відомій теоремі А. Н. Колмогорова. відповідно до якої будь-яка безперервна функція п змінних F(x₁, x₂,... x_n) може бути представлена у вигляді суми кінцевого числа одномірних функцій

(5.4.2)

де функції g_j і h_ij є безперервними й одномірними; λ_і - постійні коефіцієнти.

В 1989 р. практично одночасно декілька авторів узагальнили даний результат на багатошарові НМ, ті, яких навчають, за допомогою алгоритму зворотного поширення. Відповідно до доведеній ними теоремі, будь-яку безперервну функцію декількох змінних можна з будь-яким ступенем точності реалізувати за допомогою тришарового (уважаючи вхідний шар) персептрона, що має достатню кількість нейронів у схованому шарі.

Питання про оцінку нижньої границі складності НМ (тобто про визначення мінімально необхідного числа нейронів або кількості ваги, що набудовує НМ) у значній мірі залишається відкритим. Приведемо деякі евристичні міркування на користь вибору такої оцінки. Допустимо, що за допомогою НМ необхідно відновити вид вектор-функції Y = F(X) за результатами спостережень за вектором входів X = (х₁,х₂,...,х_n)^Т і вектором виходів Y = (y₁,y₂,...,y_m)^Т. Нехай число таких спостережень (тобто розмірність навчальної вибірки дорівнює) R, а результати спостережень Х^r = (х^r₁,х^r₂,...,х^r_n)^Т і Y^r = (y^r₁,y^r₂,...,y^r_m)^Т належать деяким обмеженим областям зміни Ω_x і Ω_y. (рис. 5.4.4).

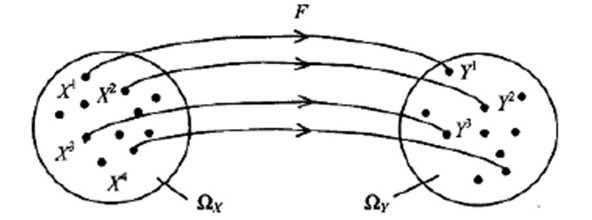
Рис. 5.4.4. Нейронне відображення F: Ω_x → Ω_y

Питання про вибір структури НМ мінімальної складності має принципове значення, оскільки:

а) у випадку (КН) < (КУ), т.т., при «заниженій» складності мережі, можна говорити лише про рішення задачі відновлення функції F з деякою погрішністю (яка тим більше, ніж простіше структура мережі);

б) у випадку (КН) » (КУ), т.т., при надмірно високій складності (надмірності) мережі, виникає ефект «перенавчання» мережі (over-learning), коли у вузлах інтерполяції (X^r, Y^r) забезпечується висока точність рішення, а в проміжках між ними функція F може поводитися досить непередбачене (наприклад, як це показано на рис. 5.4.5).

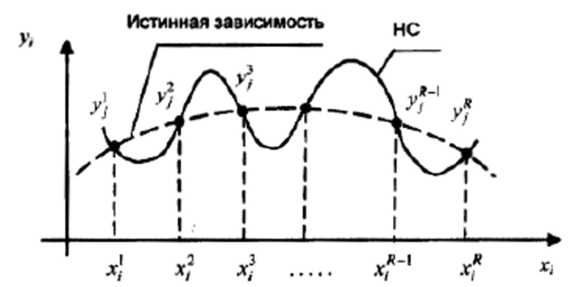
Рис. 5.4.5. Нейромережева інтерполяція функції

І останнє зауваження, пов'язане з рішенням завдання апроксимації. Багатьма авторами (зокрема. Б. Коско й Л. Вангом) показано, що в теоретичному відношенні нейронні мережі й алгоритми нечіткої логіки еквівалентні один одному, тобто одне й те ж завдання апроксимації можна вирішити з однаковою точністю, застосовуючи будь-який з цих підходів. Розходження між ними полягає в тому, що нейронні мережі навчаються на прикладах, автоматично витягаючи знання з «сирих» даних, а алгоритми нечіткої логіки базуються на визначеній системі правил, побудованих експертом, що припускає деяку попередню розбивку (осмислення) цих даних.

Можливий і проміжний варіант, коли базовий обчислювальний алгоритм будується на основі апарата нечіткої логіки, а налаштування параметрів функцій приналежності виробляється з використанням алгоритмів навчання НМ наприклад, за допомогою алгоритму зворотного поширення. Подібні схеми обчислень, називані нечіткими нейронними (або гібридними) мережами, розглядаються більш докладно в розділі 5.4.5.