Задание 2
Необходимо:
- Выбрать в структурной схеме (первое задание) расчёта участок из пяти элементов.
- Произвести расчёт функции надёжности и не надёжности (построить графики) изделия, интенсивность отказа изделия, среднее время наработки на отказ табличным методом, для выбранного участка.
- Сравнить результаты, полученные в первом и втором заданиях.
И теоретически и практически табличный метод вычисления структурной надежности является универсальным, то есть он пригоден для расчета системы любой сложности и конфигурации.
Выбираем участок структурной схемы изделия из первого задания:
Рис.5. Участок структурной схемы изделия.
В
любой строке обозначается один из
состояний,
где n-число
элементов. Множество
состояний
представляет собой полную группу
несовместных сложных событий.
Выход у характеризует состояние схемы: на выходе у будет 1, если в безотказном состоянии находятся элементы 1и, 2 и 4, или, 3 и 5.
Таблица 3 Состояние системы
№ такта |
1 |
2 |
3 |
4 |
5 |
Выход у |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
2 |
0 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
0 |
0 |
1 |
1 |
0 |
4 |
0 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
0 |
1 |
0 |
1 |
0 |
6 |
0 |
0 |
1 |
1 |
0 |
0 |
7 |
0 |
0 |
1 |
1 |
1 |
0 |
8 |
0 |
1 |
0 |
0 |
0 |
0 |
9 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
0 |
1 |
0 |
1 |
0 |
0 |
11 |
0 |
1 |
0 |
1 |
1 |
0 |
12 |
0 |
1 |
1 |
0 |
0 |
0 |
13 |
0 |
1 |
1 |
0 |
1 |
0 |
14 |
0 |
1 |
1 |
1 |
0 |
0 |
15 |
0 |
1 |
1 |
1 |
1 |
0 |
16 |
1 |
0 |
0 |
0 |
0 |
0 |
17 |
1 |
0 |
0 |
0 |
1 |
0 |
18 |
1 |
0 |
0 |
1 |
0 |
0 |
19 |
1 |
0 |
0 |
1 |
1 |
0 |
20 |
1 |
0 |
1 |
0 |
0 |
0 |
21 |
1 |
0 |
1 |
0 |
1 |
1 |
22 |
1 |
0 |
1 |
1 |
0 |
0 |
23 |
1 |
0 |
1 |
1 |
1 |
1 |
24 |
1 |
1 |
0 |
0 |
0 |
0 |
25 |
1 |
1 |
0 |
0 |
1 |
0 |
26 |
1 |
1 |
0 |
1 |
0 |
1 |
Продолжение таблицы 3
№ такта |
1 |
2 |
3 |
4 |
5 |
Выход у |
27 |
1 |
1 |
0 |
1 |
1 |
1 |
28 |
1 |
1 |
1 |
0 |
0 |
0 |
29 |
1 |
1 |
1 |
0 |
1 |
1 |
30 |
1 |
1 |
1 |
1 |
0 |
1 |
31 |
1 |
1 |
1 |
1 |
1 |
1 |
Вероятность
безотказной работы определяется как
сумма вероятностей безотказных
несовместных случайных событий, расчет
которых представлен в таблице 4.
Таблица 4 – Расчет вероятности безотказной работы
№ такта |
Вероятности безотказной работы |
21 |
|
23 |
|
26 |
|
27 |
|
29 |
|
30 |
|
31 |
|
Таким образом, вероятности безотказной работы и отказа всего изделия:
За время T=1000 часов
Интенсивность отказа изделия находится как:
1/ч.
Среднее время наработки на отказ:
ч.
Очевидным является то, что вероятность безотказной работы изделия, рассчитанного во втором задании, равна вероятности безотказной работы блока V изделия, рассматриваемого в первом задании. При этом видно, что расчет табличным методом значительно проще, чем классический метод расчета.
При сравнении полученных результатов видно, что надежность данного изделия меньше, чем изделия, рассчитанного в первом задании, так как у него отсутствует дублирующий элемент. Также у данного изделия на порядок меньше среднее время наработки на отказ и больше интенсивность отказов.
Задание 3
Для мостовой схемы необходимо:
рассчитать общую надежность изделия;
определить среднее время наработки до первого отказа;
определить среднее время наработки на отказ каждого элемента;
определить интенсивность отказа каждого элемента;
построить графики функций надежности и ненадежности;
полученные результаты сравнить с характеристиками пятью последовательно соединённых элементов (с теми же интенсивностями отказа).
Интенсивность отказа элементов берем из первого задания и время работы 1000 часов.
Рисунок
6. Мостовая схема.
Приведем вероятности безотказной работы и отказа каждого элемента:
;
;
;
;
;
;
;
;
;
.
Известно, что для информационных и глобальных систем характерны мостовые структуры.
Наиболее удобным для расчета структурной надежности мостовых схем, является метод с использованием таблиц состояний системы.
Воспользуемся понятиями теории конечных автоматов. Составим таблицу состояний элементов и состояния изделия в целом. Все наборы пронумеруем и упорядочим.
Примем:
1,2,3,4,5 – безотказное состояние элементов ( то есть = 1);
-
отказ этих элементов (то есть = 0);
Y = 1 - изделие, в котором нет отказа элементов;
Y = 0 – отказ элементов.
Также
следует указать, что число состояний m
= 2, количество элементов n
= 5, отсюда следует: k
=
.
При этом для удобства, можно в конце подсчитать только безотказную работу P(Y) или отказ Q(Y), чтобы сократить объем вычислений (в нашем случае рассчитаем P(Y)).
Таблица 5 – Таблица состояния системы
№ |
1 |
2 |
3 |
4 |
5 |
Y |
P(Yi),Q(Yi) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
0 |
1 |
1 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
0 |
1 |
0 |
1 |
0 |
|
6 |
0 |
0 |
1 |
1 |
0 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 |
|
8 |
0 |
1 |
0 |
0 |
0 |
0 |
|
9 |
0 |
1 |
0 |
0 |
1 |
0 |
|
10 |
0 |
1 |
0 |
1 |
0 |
0 |
|
11 |
0 |
1 |
0 |
1 |
1 |
0 |
|
12 |
0 |
1 |
1 |
0 |
0 |
0 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 |
|
14 |
0 |
1 |
1 |
1 |
0 |
1 |
|
15 |
0 |
1 |
1 |
1 |
1 |
1 |
|
16 |
1 |
0 |
0 |
0 |
0 |
0 |
|
17 |
1 |
0 |
0 |
0 |
1 |
0 |
|
18 |
1 |
0 |
0 |
1 |
0 |
0 |
|
19 |
1 |
0 |
0 |
1 |
1 |
1 |
|
20 |
1 |
0 |
1 |
0 |
0 |
0 |
|
21 |
1 |
0 |
1 |
0 |
1 |
0 |
|
22 |
1 |
0 |
1 |
1 |
0 |
1 |
|
23 |
1 |
0 |
1 |
1 |
1 |
1 |
|
24 |
1 |
1 |
0 |
0 |
0 |
1 |
|
25 |
1 |
1 |
0 |
0 |
1 |
1 |
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 |
|
28 |
1 |
1 |
1 |
0 |
0 |
1 |
|
29 |
1 |
1 |
1 |
0 |
1 |
1 |
|
30 |
1 |
1 |
1 |
1 |
0 |
1 |
|
31 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Таким образом, общая надежность безотказной работы всего изделия:
Рассчитаем интенсивность отказа:
1/ч.
Таким образом, функция надежности и ненадежности данной мостовой схемы выглядит следующим образом:
;
.
Построим их графически:
Таблица 6 – Расчет функции надежности для различных значений t
t,час |
P(t) |
1000 |
0,94229961 |
5000 |
0,742925 |
10000 |
0,551938 |
15000 |
0,41 |
18000 |
0,34309 |
20000 |
0,305 |
25000 |
0,226 |
30000 |
0,125 |
Рисунок 7 – Функция надежности
Таблица 7 – Расчет функции ненадежности для различных значений t
t,час |
P(t) |
1000 |
0,0577 |
5000 |
0,257075 |
10000 |
0,4481 |
15000 |
0,59 |
18000 |
0,65691 |
20000 |
0,695 |
25000 |
0,774 |
35000 |
0,875 |
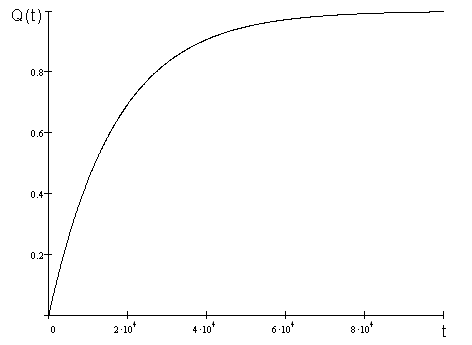
Рисунок 8 – Функция ненадежности
Для подтверждения основных выводов теории надежности приведем расчет вероятности системы, состоящей из тех же элементов, включенных параллельно.
Рисунок 9 – Структурная схема из пяти последовательно соединенных элементов
Таким образом, общая надежность безотказной работы всего изделия за время T=1000 часов:
P(1000) = 0.976*0.956*0.938*0.92*0.9=0.7247
И теоретически и практически метод, приведенный в данном расчете, является универсальным. Он пригоден для расчета схем любой сложности и конфигурации.
Очевидно при рассмотрении и сравнении мостовой и последовательной схем, можно сказать, что надежность мостовой схемы значительно превышает надежность последовательной схемы. А это, в первую очередь, свидетельствует в пользу мостовой схемы, а также подтверждает утверждение, приведенное в задании 1.
Задание 4
Под ЛПС (линейной переключательной схемой) понимается структурная схема алгоритма, построенная на элементах задержки, правило соединения, которых заключается в том, что любое число выходов любого элемента может быть соединено с любым числом входов.
Различают четыре конфигурации алгоритмов:
- без обратной связи (ЛПС –А, ЛПС – В);
- с обратной связью (ЛПС – С, ЛПС – Д).
ЛПС – А и ЛПС – В осуществляют умножение входной последовательности на некоторой характеристический полином h(x), ЛПС – С и ЛПС – Д осуществляют деление входной последовательности на характеристический полином h(x).
В задании предусмотрено исследование алгоритмов ЛПС – С и ЛПС – Д. Требуется произвести анализ надежности реализации этих алгоритмов и сравнить их. Каждой структуре соответствует характеристический полином восьмой степени.
Степень характеристического полинома соответствует числу элементов задержки в схеме (8), а число сумматоров на единицу меньше числа ненулевых членов этого полинома(4).
По заданию задаемся:
Порождающий полином:
h(x)
=
Делимый полином:
Представим
соответствующую ЛПС – Д (со встроенными
сумматорами):
Рисунок 10 – Схема ЛПС - Д
Удобной формой представления этого алгоритма является таблица действующих сигналов. Из этой таблицы можно определить для любого действующего сигнала, сколько элементарных операций он претерпел.
Величина
- число шагов перехода, определяет
сложность обработки действующих
сигналов. Автоматное реальное время
измеряется в тактах.
Каждый элемент задержки в первом полутакте записывает информацию, а во втором считывает. Таким образом, элементарными операциями является запись и считывание. Исходя из выше сказанного, рассчитывается в нижеприведенной таблице.
Таблица 8 – Действующие сигналы ЛПС – Д
t |
p(t) |
p(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z(t) |
|
0 |
- |
- |
0 |
- |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
- |
0 |
- |
- |
0 |
- |
0 |
- |
- |
- |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
3 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
4 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
5 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
18 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
28 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
42 |
8 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
62 |
9 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
90 |
10 |
- |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
129 |
11 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
185 |
12 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
264 |
Вероятности отсутствия и возникновения ошибки на каждом представлены в таблице-9 и рассчитываются по формулам:
,
,
где λ- интенсивность отказов.
Таблица – 9 Вероятности возникновения и отсутствия ошибки
t |
γ(t) |
P(t) |
Q(t) |
0 |
- |
- |
- |
1 |
1 |
0.999 |
0.001 |
2 |
3 |
0.997006 |
0.00299 |
3 |
6 |
0.994 |
0.00597 |
4 |
11 |
0.9891 |
0.0109 |
5 |
18 |
0.9823 |
0.0177 |
6 |
28 |
0.9727 |
0.0273 |
7 |
42 |
0.9597 |
0.0403 |
8 |
62 |
0.9416 |
0.0584 |
9 |
90 |
0.9176 |
0.0824 |
10 |
129 |
0.8862 |
0.1138 |
11 |
185 |
0.8452 |
0.1548 |
12 |
264 |
0.7947 |
0.2053 |
Далее приведен график зависимости вероятностей отсутствия и возникновения ошибок для данной схемы от дискретного времени.
Рис.11. – Зависимость вероятностей отсутствия и возникновения ошибок
Из графика видно, что вероятность наличия и отсутствия ошибки стремиться к максимальной энтропии, то есть к 0,5.
Зависимость числа шагов перехода от дискретного времени представлена на нижеприведенном графике:
Рис. 12. – Зависимость количества возникающих ошибок от числа тактов
Схема ЛПС-С (с вынесенными сумматорами):
Рис.13. – Схема ЛПС - С
Таблица – 10 Таблица действительности для ЛПС-С
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
- |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
0 |
- |
- |
- |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
3 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
13 |
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
15 |
9 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
20 |
10 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
29 |
11 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
39 |
12 |
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
56 |
Таблица – 11 Вероятности возникновения и отсутствия ошибки
t |
γ(t) |
P(t) |
Q(t) |
0 |
- |
- |
- |
1 |
1 |
0,99999 |
0,000010 |
2 |
3 |
0,99997 |
0,000030 |
3 |
5 |
0,99995 |
0,000050 |
4 |
7 |
0,99993 |
0,000070 |
5 |
9 |
0,99991 |
0,000090 |
6 |
11 |
0,99989 |
0,000110 |
7 |
13 |
0,99987 |
0,000130 |
8 |
15 |
0,99985 |
0,000150 |
9 |
20 |
0,9998 |
0,000200 |
10 |
29 |
0,99971 |
0,000290 |
11 |
39 |
0,99961 |
0,000390 |
12 |
56 |
0,99944 |
0,000560 |
График зависимости вероятностей отсутствия и возникновения ошибок для схемы ЛПС-С от дискретного времени:
Рисунок 14 – Зависимость вероятностей отсутствия и возникновения ошибок
Зависимость количества возможных ошибок от тактов работы для схемы с вынесенными сумматорами:
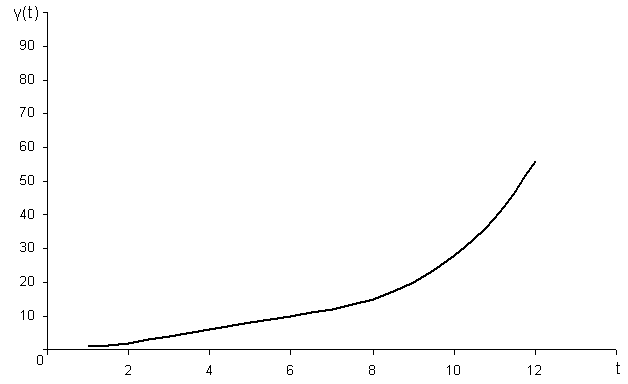
Рис.15. – Зависимость количества возникающих ошибок от числа тактов.
Как видно таблицы действительности частное от деления равно 1, а остаток равен 0. Из чего следует, что схемы ЛПС-С и ЛПС-Д действительно делят входную последовательность на характеристический полином.
Нетрудно видеть, что алгоритм реализации по структуре ЛПС-С обладает большей информационной надежностью, чем алгоритм ЛПС-Д, так как выходной сигнал z(t) для ЛПС-Д характеризуется большим числом шагов переходов (большим числом элементарных операций, которые претерпел каждый бит информации на выходе).