Задание 1
Нормально функционирующее изделие всегда может быть представлено, как некоторая структура, представляющая собой целесообразное соединение элементов. Логические, структурные схемы расчета надежности необязательно совпадают со структурной схемой самого изделия. Для расчета надежности необходимо знать интенсивности отказа или безотказной работы элементов, и время работы.
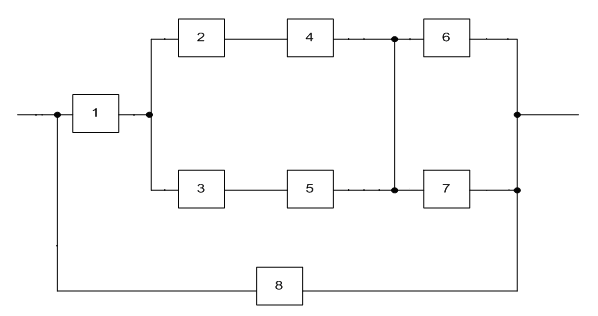
Рис. 1. Структурная схема расчета надежности изделия.
Интенсивности безотказной работы элементов:
1/ч;
1/ч;
1/ч
;
1/ч;
1/ч;
1/ч
;
1/ч.
Время работы: t = 1000 часов.
Необходимо:
сформулировать условия безотказной работы при одинаковом t;
рассчитать общую надежность изделия;
определить среднее время наработки на отказ;
определить интенсивность отказа изделия;
построить графики функций надежности и ненадежности.
Перед расчетом сформулируем условие безотказной работы:
устройство будет безотказно работать, если в безотказном состоянии будет находиться элемент 1 и, 2 и 4, или,3 и 5, и, 6 или 7,или хотя бы элемент 8.
Так как в изделии элементы имеют последовательно-параллельные соединения, то можно применить метод преобразования структурной схемы (декомпозицию), объединяя элементы в более крупные блоки и применяя формулы расчета для элементарных схем надежности.
Для последовательного соединения:
|
|
|
Для параллельного соединения:
|
|
|
Произведем декомпозицию структурной схемы, для чего разобьем ее на последовательные и параллельные соединения элементов. Получим:
Рис. 2. Структурная схема изделия после декомпозиции
Длалее необходимо рассчитать вероятность безотказной работы каждого отдельного элемента по формуле:
.
Таким образом, имеем:
=
0.976 , аналогично вычисляем надежности
остальных элементов, в результате чего
получаем:
0,956;
0,938;
0,92;
0,9;
0,882;
0,859.
Рассчитаем надежности структурных блоков, представленных на схеме. Параллельное соединение равнозначно функции дизъюнкции, а последовательное – конъюнкции.
;
;
;
;
;
;
;
.
Исходя из полученной вероятности всего изделия, получим его интенсивность отказов:
1/ч.
Среднее время наработки на отказ:
ч.
Функции надежности и ненадежности выглядят следующим образом:
,
Таблица 1. Расчет функции надежности для различных значений t
t,ч |
P(t) |
1 |
0,999996 |
10 |
0,9999659 |
50 |
0,9998 |
100 |
0,99966 |
1000 |
0,996596 |
10000 |
0,966475 |
100000 |
0,7110589 |
150000 |
0,599596 |
200000 |
0,5056 |
250000 |
0,42635 |
300000 |
0,3595 |
350000 |
0,3032 |
400000 |
0,25564 |
Таблица 2 - Расчет функции ненадежности для различных значений t
t,ч |
Q(t) |
10000 |
0.0335 |
100000 |
0.2889 |
150000 |
0.4 |
200000 |
0.49 |
250000 |
0.5737 |
300000 |
0.64 |
350000 |
0.6968 |
400000 |
0.744 |
1000000 |
0.96696 |
По полученным таблицам построим функции надежности и ненадежности:
Рис. 3. Функция надежности изделия.
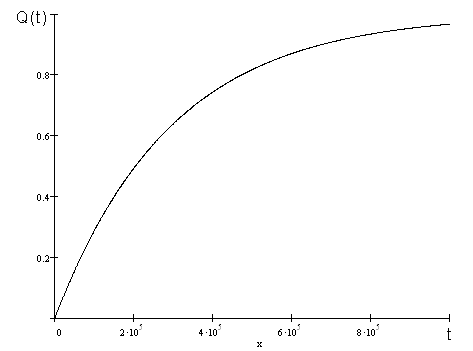
Рис. 4. Функция ненадежности.
Из вышеприведенных расчетов и построенных графиков, очевидно, что выполняется одно из основных положений теории надежности: при параллельном соединении элементов общая надежность всегда выше надежности самого надежного элемента, а при последовательном соединении общая надежность всегда меньше надежности самого ненадежного элемента.