10. Частотные характеристики сар

В качестве входных воздействий здесь выбираются гармонические (синусоидальные) воздействия. На это есть несколько причин:

1. большинство реальных воздействий может быть представлено в виде суммы гармоник различных частот (разложением в ряд Фурье);

2. в установившихся режимах гармонические сигналы передаются линейными элементами и системами без искажения формы;

3. не представляет затруднений исследовать поведение линейных элементов и систем при гармонических воздействиях и экспериментально.

Пусть на вход стационарного линейного элемента воздействует гармонический сигнал вида: , где и Т – его амплитуда, фаза, угловая частота и период. Тогда на выходе с течением времени устанавливается гармонический сигнал той же частоты: , но (в общем случае) с другой амплитудой и фазой.

Изменение амплитуды и фазы зависит как от свойств объекта (его диф. уравнения и параметров), так и от угловой частоты сигнала.

Отношение

(1.5.1)

при изменении частоты  от 0 до  называют амплитудно-частотной, а разность

, (1.5.2)

– фазочастотной характеристиками данного элемента или системы.

Амплитудно-частотная A() и фазочастотная () характеристики показывают, как линейный элемент или система изменяют амплитуду и фазу гармонического сигнала: амплитуда уменьшается или увеличивается (в А раз) и сдвиг по фазе увеличивается или уменьшается на  градусов (или радиан).

При этом сами частотные характеристики A() и () зависят только от свойств этого элемента или системы и не зависят от амплитуды и фазы входных гармонических сигналов. Исключив из уравнений (1.5.1) и (1.5.2) частоту  получим зависимость:

, (1.5.3)

которую называют амплитудно-фазовой характеристикой.

Частотные характеристики всякого элемента (системы) связаны с их передаточными функциями. Подставив в передаточную функцию W(s) вместо s мнимую частоту j, получим комплексную функцию , которую называют частотной передаточной функцией или комплексным коэффициентом передачи. При каждом значении j_i она является комплексной величиной, которую можно записать в показательной форме:

,

где , а , т.е. модуль и аргумент частотной передаточной функции представляют собой амплитудно-частотную и фазочастотную характеристики.

Функция может быть представлена и в алгебраической форме записи как , где , и V() = Im называют соответственно вещественной (действительной) и мнимой частотными характеристиками. Они не имеют конкретного физического смысла, но их удобно использовать при расчетах.

Годограф функции [геометрическое место точек (траектория) конца вектора при изменении частоты от 0 до ] – называется амплитудно-фазо­вой частотной характеристикой (АФЧХ) (рис. 8).

Эту характеристику строят на комплексной плоскости в декартовых или полярных координатах. В 1-ом случае по оси абсцисс откладывают вещественную ЧХ U(), по оси ординат – мнимую ЧХ V(). Во 2-ом случае – проводят вектор длиной A()под углом , причем угол отсчитывается от положительной полуоси абсцисс против часовой стрелки.

В се частотные характеристики связаны между собой соотношениями:

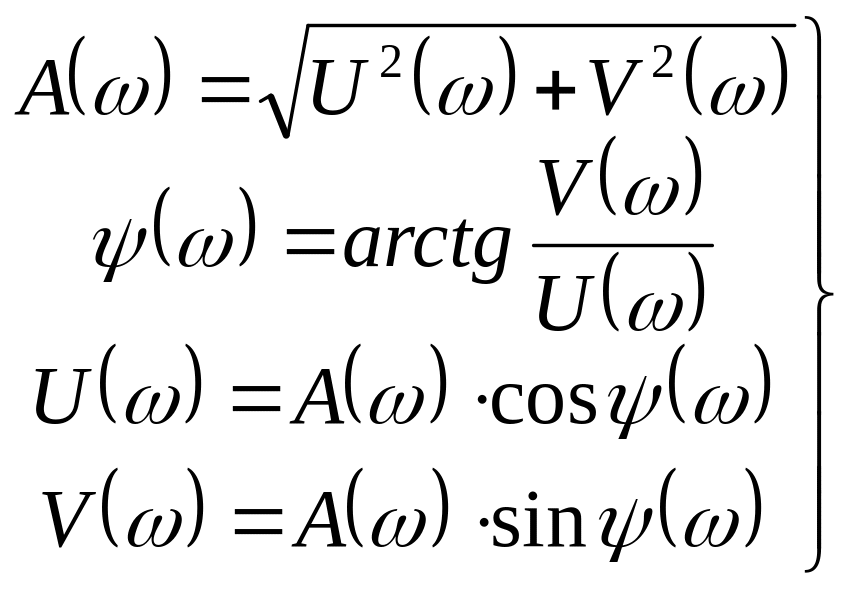
При графическом построении частотных характеристик широко пользуются логарифмическими масштабами, а построенные характеристики называют логарифмической амплитудно-частотной (ЛАЧХ) и логарифмической фазочастотной (ЛФЧХ) характеристиками. При этом по оси абсцисс графика наносят отметки, соответствующие lg, но около меток указывают значения самой . Отрезок оси абсцисс, соответствующий изменению частоты в 10 раз, называется декадой, изменению частоты в 2 раза – октавой.

Для ЛАЧХ по оси ординат откладывают в равномерном масштабе логарифмическую амплитуду: L = 20 lgA, [dB].

На таком графике начало координат расположено специфично. Нуль логарифмической амплитуды соответствует значению А=1. Нуль оси абсцисс лежит слева в бесконечности (т.к., ), поэтому вертикальная ось может помещаться в любой точке. Обычно её выбирают так, чтобы график охватывал нужный диапазон частот.

Для ЛФЧХ ось абсцисс размечают также, а по оси ординат в равномерном масштабе откладывают фазу в градусах (или радианах). Обычно ЛФЧХ строят под графиком ЛАЧХ, чтобы изменение фазы можно было сопоставить с изменением амплитуды.

Для построения асимптотической ЛАЧХ нужны лишь весьма простые вычисления. Для получения эквивалентной ЛАЧХ двух последовательно соединенных звеньев можно очень просто графически суммировать характеристики ЛАЧХ каждого звена (т.к. ).

Типичные асимптотические ЛАЧХ имеют следующие графики:

1. При значении модуля частотной передаточной характеристики . Здесь L=20lg k есть постоянная величина, а ЛАЧХ представляет собой прямую, параллельную оси абсцисс (рис. 9а).

2. П ри . Здесь L=20lgk-20lg; при имеем L=20lg k и на протяжении одной декады (с увеличением частоты 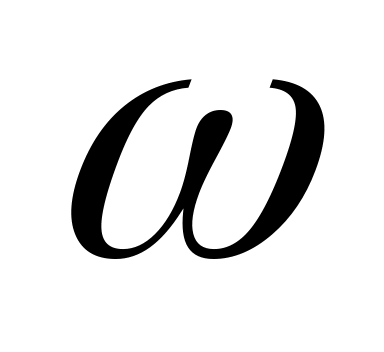в 10 раз) 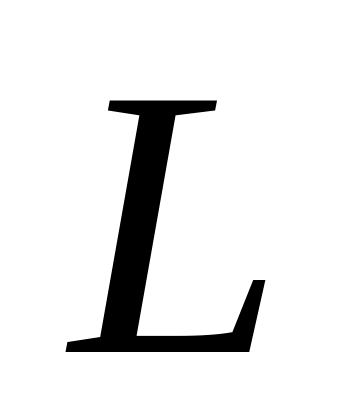уменьшается на 20 dB. ЛАЧХ представляет собой бесконечную прямую с наклоном, равным -20 dB/дек, проходящую через точку с координатами [1; 20lgk] (рис. 9б).

3. П ри 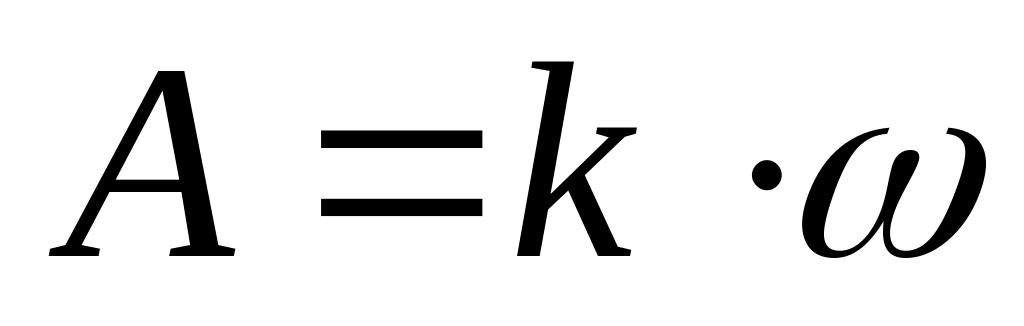имеем: L = 20lgk -20lg ; всё как в предыдущем случае, только наклон составит +20 дB/дек (рис. 9в).

4. П ри . Получается, что . При малых частотах, когда 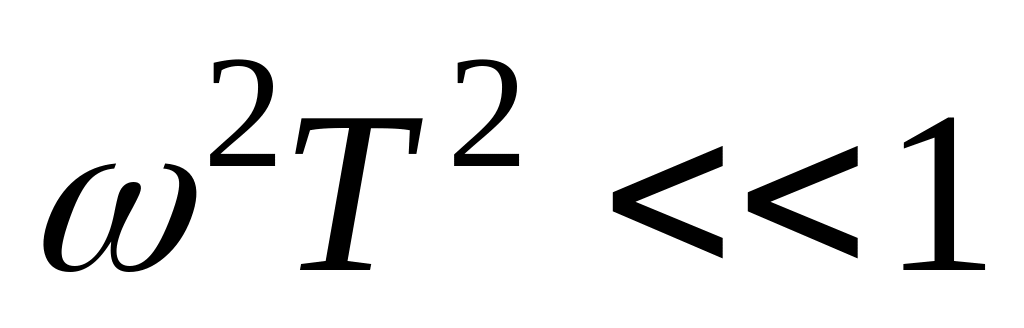, имеем L=20lg k ; на больших частотах (при ) 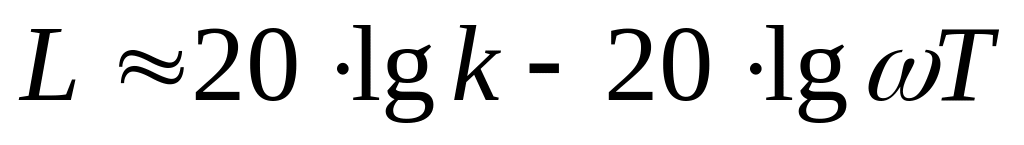. На частоте «среза» асимптоты сопрягаются (рис. 9г).

5. При будем иметь 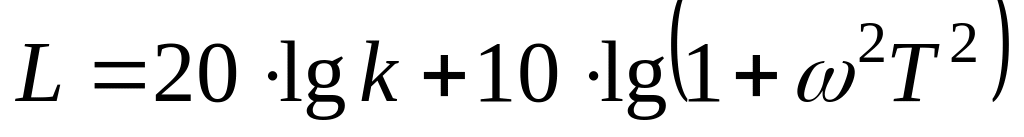. Всё, как в предыдущем случае, только 2-я асимптота имеет положительный наклон (рис. 9д).

П ри , когда 0< <1. Здесь выражение для ЛАЧХ будет На малых частотах L=20lgk, на высоких . Асимптоты сопрягаются на частоте среза , причем вторая асимптота имеет наклон -40 dB/дек (рис. 9е).