1. Понятие "объект управления". Задача управления и задача регулирования

объект управления (ОУ), т.е. некий механизм, агрегат или устройство, некоторый технологический, энергетический или транспортный процесс, для которого должно быть обеспечено желаемое поведение.

Задача управления заключается в формировании такого закона изменения управляющих воздействий, при котором поведение объекта достигается независимо от изменения поступающих на него возмущений.

Задача регулирования состоит в том, чтобы одну или несколько выходных величин объекта регулирования сделать равными некоторым эталонным функциям времени (задающим воздействиям).

2. Функциональные схемы: разомкнутой сар, разомкнутой с измерением основного возмущения, замкнутой сар

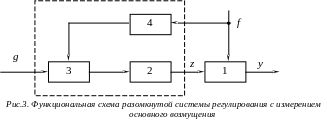
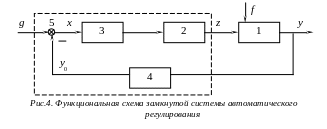
3. Классификация сар

а) по принципу действия различают разомкнутые, замкнутые и комбинированные системы;

б) по цели регулирования – системы стабилизации, программного регулирования и следящие;

в) по характеру сигналов в регуляторе – непрерывные, релейные и дискретные (импульсные и цифровые);

г) по классу диф. уравнений, описывающих динамику системы – линейные и нелинейные: у линейной системы динамика всех элементов описывается линейными диф. и алгебраическими уравнениями.

д) по количеству регулируемых величин – различают одномерные и многомерные (многосвязные) системы;

е) кроме того, системы различаются по статическим свойствам (статические и астатические) и законам регулирования (П, И, ПИ, ПД, ПИД и т.д.).

4. Линеаризация статических характеристик и нелинейных диф. Уравнений элементов сар Линеаризация статических характеристик и диф. Уравнений

Ч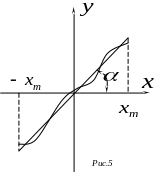 асто встречаются элементы, у которых нелинейна лишь статическая характеристика, т.е. зависимость выходной величины от входной величины в установившемся режиме. Если на некотором участке нелинейная характеристика может быть аппроксимирована прямой с удовлетворительной точностью, то эта прямая и принимается за статическую характеристику данного элемента (рис.5). Следовательно, приближенно , где . Такую простую линеаризацию (метод осреднения) используют в инженерной практике всегда, когда гладкая, но достаточно сложная по виду характеристика не имеет аналитического описания (алгебраического уравнения).

Другой метод – малых отклонений – применяют для линеаризации существенно нелинейных статических характеристик и нелинейных диф. уравнений. Дело в том, что в устойчивых системах АР отклонения входных и выходных воздействий от их базовых значений принципиально достаточно малы. Поэтому при таких малых отклонениях любую систему в известных пределах можно считать линейной. Это положение строго доказывается математически (разложением в ряд Тейлора), но мы это опустим. Отметим лишь, что метод малых отклонений неприменим, если линеаризуемая функция имеет разрывы непрерывности или неоднозначность по какой-либо из переменных (например, в импульсных и релейных системах).