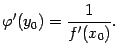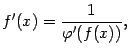43. Дайте вывод формулы производной сложной функции.

Производная сложной функции

"Двухслойная" сложная функция записывается в виде где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.

44. Выведите формулу производной обратной функции.

Пусть   -- непрерывная функция, монотонная на интервале  . Тогда, как мы доказали в гл. 3, функция   имеет обратную функцию  , которая также является непрерывной и монотонной функцией на интервале  , в который функция   переводит интервал  . Пусть   -- фиксированная точка и   -- точка, ей соответствующая. Тогда  .

        Теорема 4.5   Пусть функция   имеет в точке   производную  . Тогда обратная функция   имеет в соответствующей точке   производную  , которую можно отыскать по формуле

(4.14)

        Доказательство.     Дадим аргументу   приращение  , такое что  , и рассмотрим соответствующее приращение  , определяемое равенством  . Тогда, очевидно,  ; при этом  , а из монотонности функции   следует, что  . Поскольку как функция  , так и функция   непрерывны, то условия   и   эквивалентны. Составим теперь разностное отношение для функции   и запишем для него очевидное равенство:

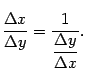
Теперь перейдём в этом равенстве к пределу при   и учтём, что при этом   тоже стремится к 0:

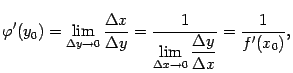
что мы и хотели доказать.      

Заметим, что, очевидно, из формулы (4.14) следует, что

(4.15)

если   -- функция, обратная к  .

45. Приведите пример функции, заданной неявно. Объясните, как найти ее производную.

Определение

Если независимая переменная   и функция   связаны уравнением вида  , которое не разрешено относительно  , то функция   называется неявной функцией переменной  .

Пример

Всякую явно заданную функцию   можно записать в неявном виде  . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение   не разрешимо относительно  , оказывается возможным найти производную от   по  . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию  как функцию от  , а затем из полученного уравнения найти производную  .

Пример

Задание. Найти вторую производную   неявной функции  .

Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что  является функцией переменной  , поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем:

Из полученного равенства выражаем  :

Для нахождения второй производной продифференцируем равенство   еще раз:

Подставив вместо   найденное выше выражение, получаем:

После упрощения получаем:

Из полученного равенства выражаем вторую производную  :

Ответ. 

46. Приведите пример функции, заданной параметрически. Объясните, как найти ее производную.

Определение

Предположим, что функциональная зависимость   от   не задана непосредственно  , а через промежуточную величину —  . Тогда формулы

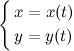
задают параметрическое представление функции одной переменной.

Пусть функция   задана в параметрической форме, то есть в виде:

где функции   и   определены и непрерывны на некотором интервале изменения параметра  . Найдем дифференциалы от правых и левых частей каждого из равенств:

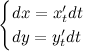
Далее, разделив второе уравнение на первое, и с учетом того, что  , получим выражение для первой производной функции, заданной параметрически:

Для нахождения второй производной   выполним следующие преобразования:

Пример

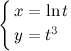Задание. Найти вторую производную   для функции   заданной параметрически.

Решение. Вначале находим первую производную   по формуле:

Производная функции   по переменной   равна:

производная   по  :

Тогда

Вторая производная равна

Ответ. 

47. Найдите производные указанных функций

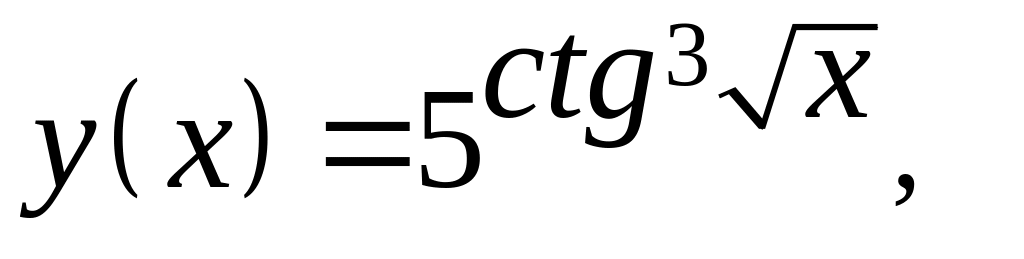
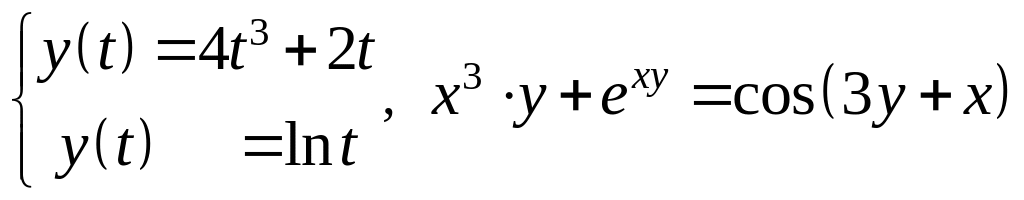
48. Сформулировать теорему о разложении функции по формуле Тейлора с остаточным членом в форме Пеано.

Разность между функцией   и её многочленом Тейлора называется  -м остатком, или  -м остаточным членом; обозначим этот остаток через  :

Формула  , в более развёрнутой форме имеющая вид

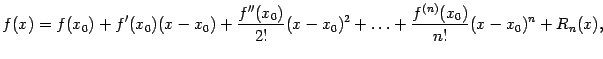
называется формулой Тейлора для функции   в точке  , а представление функции   в таком виде -- её разложением по формуле Тейлора.

Если считать, что остаток   мал, то его можно отбросить без большой погрешности; при этом получается приближённая формула

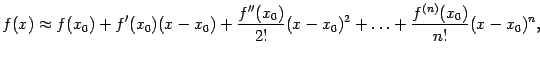
дающая возможность для приближённого нахождения значений функции  .

Выясним, в каком смысле можно понимать "малость" остатка   в формуле Тейлора, чтобы этой приближённой формулой мы могли пользоваться осмысленно.

        Теорема 6.1 (формула Тейлора с остаточным членом в форме Пеано)   Пусть   -- остаток в формуле Тейлора для функции   в точке  , и функция   имеет непрерывную  -ю производную. Тогда   -- бесконечно малая величина того же или большего порядка малости, как  , при  . (Остаточный член  , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.)

49. Что такое формула Маклорена?

Формула суммирования Эйлера — Маклорена — формула, позволяющая выражать дискретные суммы значений функции через интегралы от функции. В частности, многие асимптотические разложения сумм получаются именно через эту формулу.

Формула Эйлера — Маклорена имеет вид:

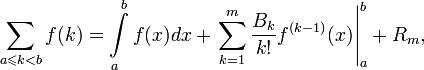
где

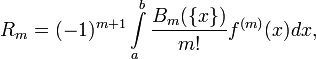
здесь   — натуральное,   — числа Бернулли,   — достаточно гладкая функция, чтобы иметь производные  ,   — многочлен Бернулли,   — дробная часть x. В случае, когда   мало, получаем хорошее приближение для суммы.

Многочлены Бернулли   определяются рекуррентно как

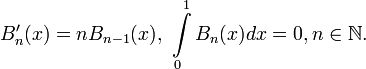
Выражение   называется периодической функцией Бернулли.