6.3.2 Концепція коінтеграція

Наявність трендів у тимчасових рядах, мабуть, можна розглядати як головну проблему емпіричної економетрії. Тренди, як стохастичні, так і детерміновані, можуть стати причиною помилкових регресій.

Але в наявності неспростовний факт: в економіці більша частина тимчасових рядів містить тренди якого-небудь типу. Для рятування від тренда можна виконати перетворення у вигляді переходу до різниць такого порядку, які будуть стаціонарними.

Але це не краще рішення. Застосування оператора узяття, наприклад, перших різниць до змінного приводить до втрати довгострокових властивостей процесів, тому що модель у перших різницях не має довгострокового рішення.

Прагнення одержати модель, що враховувала б короткострокові й довгострокові особливості процесів і в той же час підтримувала б стаціонарність всіх змінних, підштовхнуло до перегляду принципів побудови регресії.

Цей підхід ґрунтується на таких економічних даних, які, будучи нестаціонарними, можуть бути скомбіновані в один ряд, що буде вже стаціонарним. Ряди, що володіють такою особливістю, називаються коінтегрованими рядами .

Якщо, наприклад, виявляється, що змінні є I(1) - інтегрованими першого порядку й звичні методи регресійного аналізу до них не підходять, то в цьому випадку використовують так звану коінтеграційну регресію.

Процеси I(1) є коінтегрированими першого порядку [З(1,0)], якщо існує їхня лінійна комбінація, що є I(0), тобто стаціонарна.

Тобто Y і X, що є I(1), коінтегровані, якщо існує множник , такий, що є I(0).

Легко зобразити на малюнку два таких нестаціонарних I(1) процеси, які зв'язані один з одним стаціонарною лінійною комбінацією с. У цьому випадку, як би будуть «рухатися паралельно» у часі.

Приклад рядів, лінійна комбінація яких нестаціонарна.

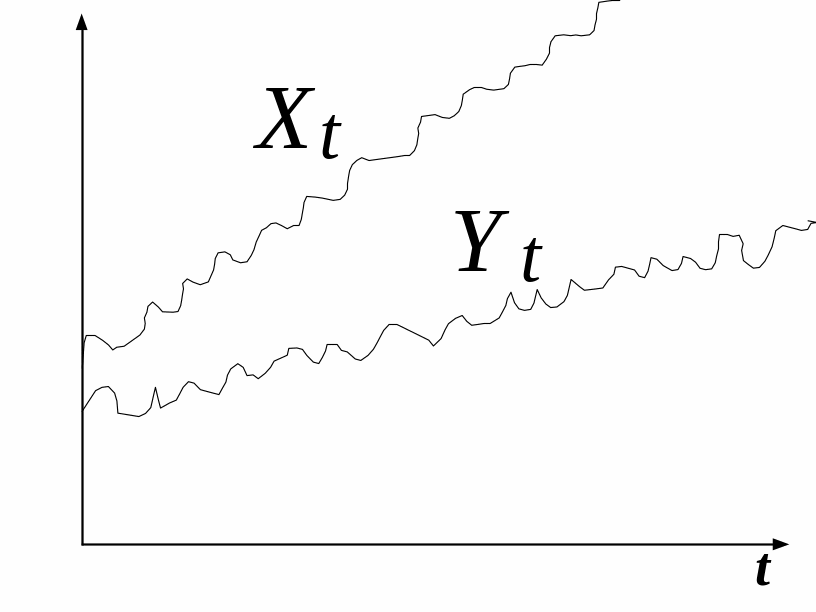
Однак у другому випадку можна підібрати таке , що різниця буде стаціонарною. Наприклад,

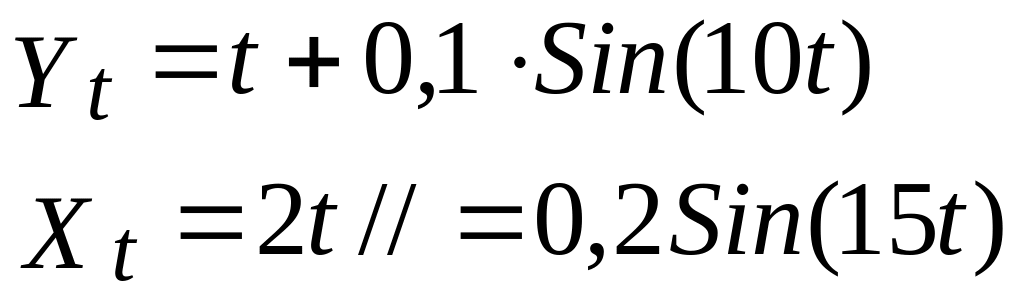
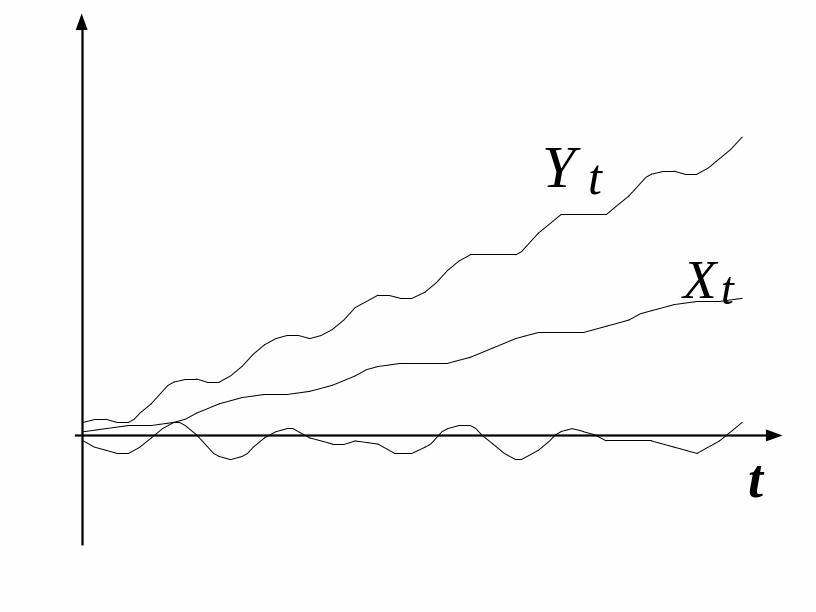
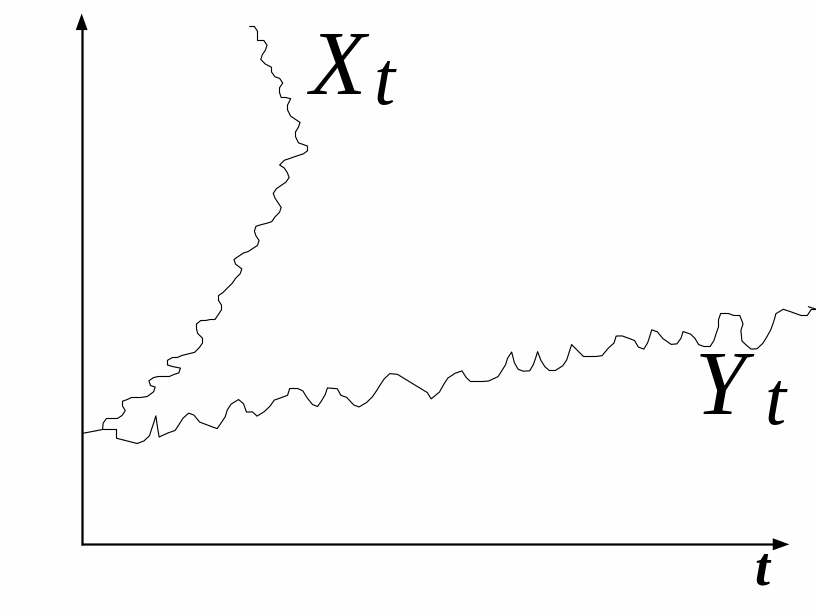
Різниця буде стаціонарною (це можна перевірити на комп'ютері), тобто при змінні можуть і не змінюватися в часі однаково, точніше один змінна може рости швидше іншої. Але!!!

Очевидно, що коінтегрованими можуть бути тільки такі два тимчасових ряди, які інтегровані однакового порядку. Якщо одна змінна I(1), а інша - I(2), вони не можуть бути коінтегрованими.

Формальне визначення коінтеграції двох змінних, розроблене Энглом і Грейнджером (1987).

Тимчасові ряди називаються коінтегрованими порядку d, b, де , - позначається: , якщо:

Обоє тимчасових ряду інтегровані порядку d;

Існує лінійна комбінація цих змінних , котра інтегровані порядку (d-b).

Вектор [ ] називається коінтеграціоним вектором.

Узагальнимо це визначення для випадку n змінних.

Нехай - вектор розмірності [n+1], що включає , причому

Кожна змінна - I(d)

Існує ( )-мірний вектор такий, що - I(d,b), тобто - CI(d,b).

На практиці найцікавіша ситуація, коли ряди трансформовані за допомогою коінтегрующего вектора, стаціонарні, і d = b, а коінтегрующій коефіцієнти, що становлять коінтегрующій вектор, можуть бути визначені на основі довгострокової залежності між змінними.

Зупинимося на ситуації, коли все - I(d).

Якщо - I(1), і довгострокова залежність між ними визначається як

(1)

те коінтегрующій вектор [ ] і відхилення від довгострокової траєкторії - I(0), тобто стаціонарно.

Тут, на цьому етапі важливо показати, що лінійна комбінація дійсно стаціонарна. Для цього пропонується застосувати метод Дикі-Фулера до залишків з коінтеграційною регресіеєю

Тест Энгла-Грейнджера проводиться за допомогою регресії

Розподіл t-статистики для гіпотези в цій регресії буде відрізнятися від розподілу DF-Статистики, але є відповідні таблиці.

Нульовою гіпотезою, отже, є відсутність коінтеграції (відсутність стаціонарності, )

Якщо гіпотеза про відсутність коінтеграції відкидається, то отримані результати не є помилковою регресією.

Після цього можна оцінити модель виправлення помилок, що робить змінні коінтегрованими. У цій моделі (регресії) використовуються перші різниці вихідних змінних і залишки з коінтеграційної регресії, які будуть представляти коригувальний член моделі виправлення помилок.

(2)

Тут залежна змінна й регрессори й - I(0). І тому немає небезпеки одержання помилкової (помилкової) регресії через наявність стохастичного або детермінованого тренда в даних. У такій регресії t-статистики й F-статистики будуть мати звичайні асимптотичні розподіли й можна використовувати їх для перевірки гіпотез про модель. (але не варто намагатися перевіряти гіпотези за допомогою статистик, отриманих у коінтеграційної регресії).

До появи методу Энгла-Грейрджера дослідники, не підозрюючи про те, часто одержували помилкові регресії, або ж оцінювали регресії в нових різницях, що, хоча й приводило до стаціонарності змінних, але не давало можливості враховувати стаціонарний коригувальний член, тобто регресійна модель була невірно специфікована (проблема пропущеної змінної). Тим самим підкреслюється роль коригувального елемента (передбачається, що якщо в попередній період змінна Y відхилилася від свого довгострокового значення, то член коректує динаміку в потрібному напрямку).

Модель включає довгострокове рішення й механізм коректування (виправлення) помилки, якщо _­­­.

Можливі різні варіанти сполучення й коінтеграції в розглянутій моделі (2).

1. Якщо ~ I(1), а ~ I(0), то u_t ~ I(1), і змінні й коінтегровані.

2. Якщо ~ I(1), а ~ I(1), то можливо, що u_t ~ I(0) і змінні й коінтегровані, тільки якщо коінтегруючий вектор дорівнює [λ,-1].

3. Якщо ~ I(0), а ~I(0), то u_t ~ I(0), і про коінтеграції не можна ніщо сказати.

4. Якщо ~ I(0), а ~ I(1), то u_t ~ I(1), і змінні й некоінтегровані.

Отже, у довгостроковій залежності між двома змінними обидві повинні бути інтегровані одного порядку, щоб ряд помилок був I(0).

Стаціонарність помилок особливо важлива, якщо будується модель, що передбачає механізм виправлення помилки.

Завдання істотно ускладнюється, якщо кількість змінних, що включаються в довгострокову залежність, збільшуються.

Розглянемо випадок трьох змінних:

(3)

У цьому випадку допускається, щоб порядок інтеграції в змінних був різним, а ряд помилок був при цьому стаціонарним.

Нехай ~ I(0), ~ I(1) ~ I(1). За аналогією з попереднім аналізом, можна чекати, що u_t ~ I(1). Може, однак, трапитися, що становить коінтегруючий вектор для й , і тоді лінійна комбінація ~ I(0), тому що й ~ I(1) інтегровані одного порядку. У цьому випадку буде стаціонарна, тому що ~ I(0) і ~ I(0). В економіці більше поширена ситуація, коли ~ I(1), ~ I(2) і ~ I(2). Незважаючи на різні порядки інтеграції, змінна помилок буде стаціонарної, тому що ~ I(1). Т.е. якщо , ~ СI(2) з коінтегруючим вектором .