Стохастичний тренд

Допустимо, є вибіркові значення від до й ми хочемо пророчити майбутні значення тимчасового ряду. На момент часу t, оптимальним прогнозом буде умовне математичне очікування :

, (тому що )

Отже, постійна величина - безстороння оцінка для майбутніх значень для всіх S>0. Для інтерпретації помітимо, що збурювання має постійний вплив на всі наступні значення . Мультиплікатор впливу (impact multiplier) на (тобто ) – той же самий, що мультиплікатор на все . Це сталість на пряму відбивається на функції пророкування для . У літературі по тимчасових рядах така послідовність, як говорять, містить стохастичний тренд, якщо вираження повідомляє постійне (хоча й випадкове) зміна в умовне математичне очікування (середню) ряду.

Різні ряди з динамікою темпів не мають особливої тенденції до росту або зниження; так само як не мають якої-небудь тенденції до повернення до даного середнього рівня.

6.2.2 Модель випадкового блукання із дрейфом

Тепер допустимо, що зміни в Y частково детерміновані й частково стохастичні.

Модель випадкового блукання із дрейфом виходить (перетвориться) з моделі випадкового блукання додаванням константи :

(3)

Якщо дано початкове значення , загальне рішення для буде:

(4)

Тут поводження визначається двома нестаціонарними компонентами: лінійним детермінованим трендом і стохастичним трендом .

Якщо ми візьмемо математичне очікування, середнє значення буде , а середнє значення дорівнює (це треба з того, що )

Помітимо, що перша різниця ряду стаціонарна; перехід до першої різниці створює стаціонарну послідовність .

Ясно, що динаміку тимчасового ряду визначає детермінований тренд. У дуже більших вибірках, асимптотична теорія припускає, що це, у всякому разі, має місце. Однак не слід думати, що завжди легко (розпізнати) розрізнити модель випадкового блукання й модель випадкового блукання із дрейфом. У малих вибірках, збільшення дисперсії або зменшення абсолютного значення може перекривати довгострокові властивості послідовності. Помітимо, що багато рядів – включаючи пропозицію грошей і реальний ВНП (GNP) – поводяться як модель випадкового блукання із дрейфом.

ФУНКЦІЯ ПРОГНОЗУВАННЯ

Замінимо в (4) t на t+S:

Взявши умовне математичне очікування від , одержимо

По контрасту із чистою моделлю випадкового блукання, що прогнозує функція не є категорична пряма. Той факт, що середня зміна в завжди константа , відбивається на прогнозі. До того ж взявши за основу, ми прогнозуємо цю детерміновану зміну на S кроків уперед. Отже, модель не містить нерегулярний компонент; випадкове блукання із дрейфом містить тільки детермінований тренд і стохастичний тренд.

6.2.3 Модель випадкового пошуку із шумом

У моделі випадкового блукання із шумом є сума стохастичного тренда й компонента білого шуму. Формально ця третя модель представляється як

(5)

(6)

де - процес білого шуму з дисперсією рівної й і незалежно розподілені для всіх t і S, тобто .

Легко перевірити, що послідовність являє собою стохастичний тренд. При відомій початковій умові , рішення для є

Поєднуючи це вираження з білим шумом, маємо:

Тепер допустимо, що в момент t=0 значення задається , так що рішення для моделі випадкового блукання із шумом може бути записане як

(7)

Ключові властивості цієї моделі такі:

1. Безумовна середня послідовності константа:

і прогноз на S періодів:

Помітимо, що наступні один за іншим збурювання мають постійний вплив на . Отже, є стохастичний тренд .

2. Послідовність має компоненту чистого шуму, і послідовність має тільки тимчасовий ефект із позиції впливу на . Поточна реалізація впливає тільки на , але не на наступні .

3. Дисперсія не постійна:

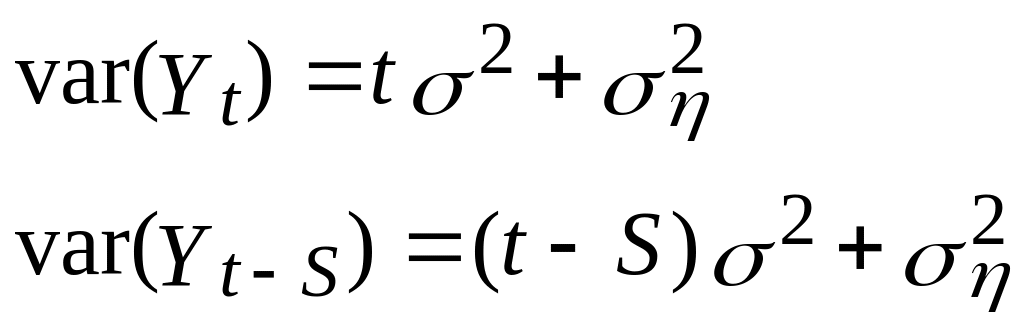
Як і в інших моделях зі стохастичним трендом, дисперсія в міру збільшення t росте нескінченно. Наявність компонента білого шуму означає, що коефіцієнт кореляції між і менше, ніж для чистої моделі випадкового блукання.

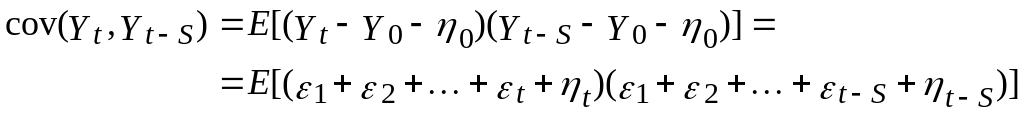
Т.к. і незалежні послідовності білого шуму,

і коефіцієнт кореляції

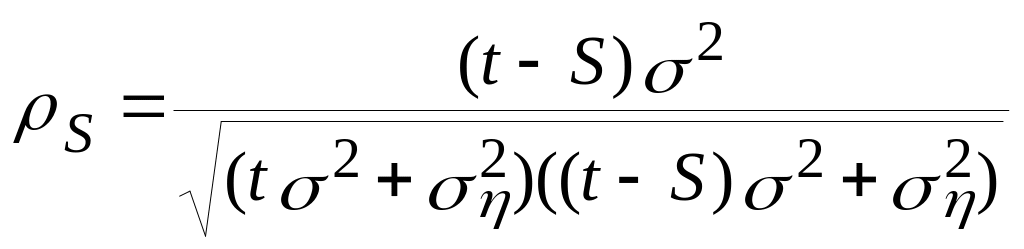
Порівняння з (2) - для моделі чисто випадкового блукання – підтверджує, що автокореляції для моделі випадкового блукання із шумом завжди менше для .

ФУНКЦІЯ ПРОГНОЗУ

Нехай відомі вибіркові значення

Взявши умовне математичне очікування, одержуємо

Таким чином, модель випадкового блукання із шумом містить і тренд, і іррегулярний компонент. Звичайно, має часовий ефект тільки на ; прогноз - поточне значення зменшене на . Постійний компонент - стохастичний тренд .