6 Динамічні регресійні моделі

6.1 Авторегресійна модель із розподіленим лагом

6.1.1 Модель розподіленого лага

У моделі на зміну досліджуваної змінної y впливає не тільки якийсь пояснюючий фактор х, але і його лаги. Тоді модель розподіленого лага ADL можна записати так:

- у векторній формі, (1)

де , де q – величина максимального лага.

Коефіцієнти показують структуру лага й називаються вагами.

У випадку мультиколінеарності лагових змінних звичайно на лагову структуру накладають яке-небудь обмеження, щоб не зменшувати кількість оцінюваних параметрів.

6.1.1.1 Поліноміальний лаг

(2)

- коефіцієнти;

- ступінь багаточлена.

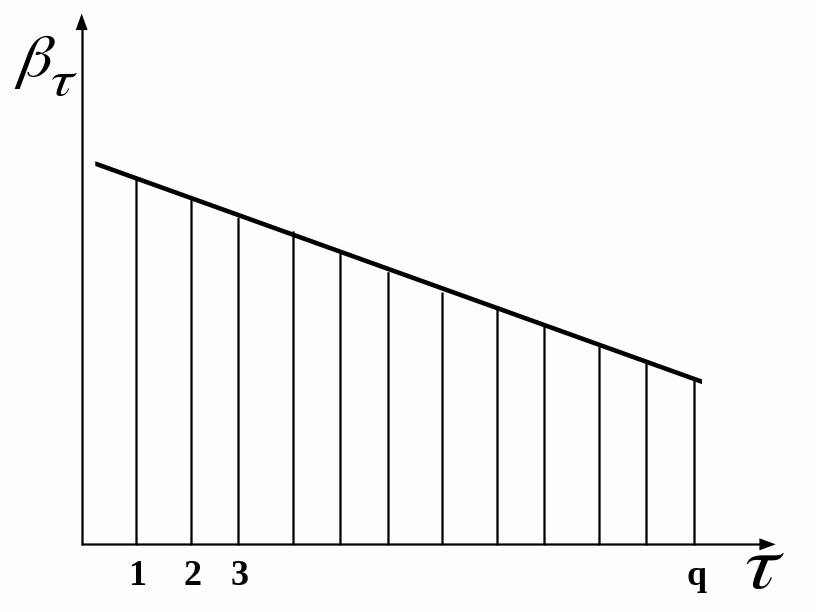
Найпростіший поліноміальний лаг – лінійний, для якого .

Щоб оцінити таку модель, підставимо вираз для у формулу (1), тобто у вихідну модель:

,

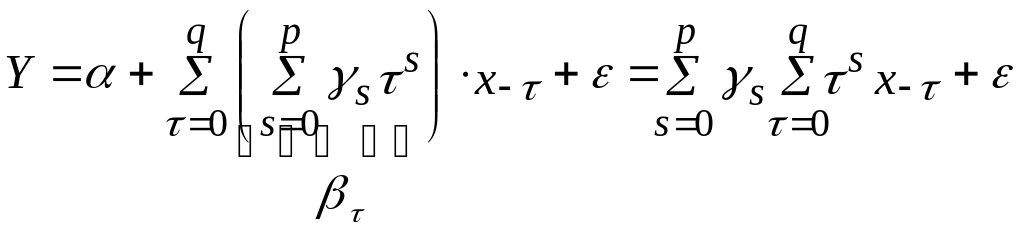т.п. виходить нова змінна

(3)

де , тобто - це перетворені регресори, їхнього значення завжди можна одержати, отже, ми можемо оцінити значення методом найменших квадратів. Підставивши їх в (2), знайдемо величину ваг .

6.1.1.2 Експонентний лаг (геометричний лаг)

Його ваги задаються наступним співвідношенням: .

Т.е. ваги геометричного лага убувають експоненціально зі збільшенням лага, а не лінійно.

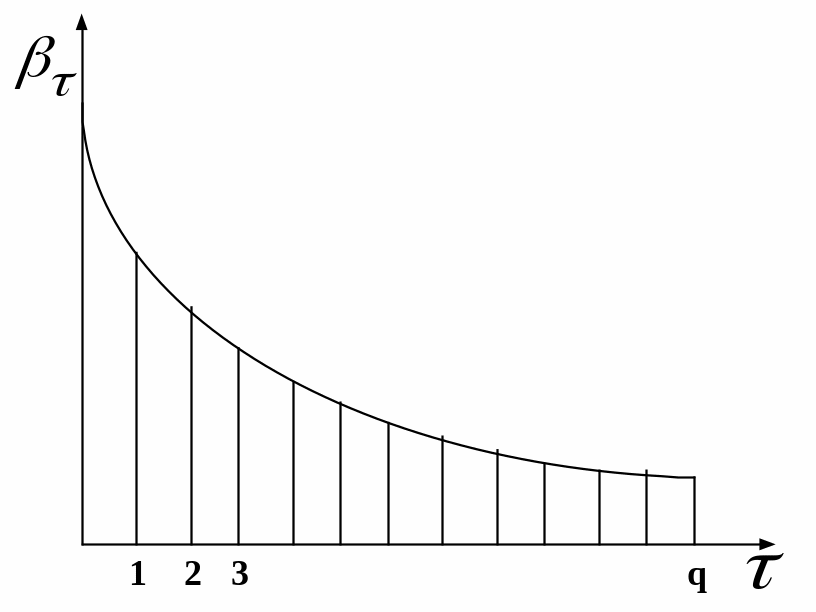
У моделі з геометричним лагом можна застосувати перетворення Койко (Koyck transformation).

Після цього перетворення модель із розподіленим лагом буде виглядати так:

(4)

(модель із експонентної лаговою структурою після перетворення Койко)

(5)

Помножимо обидві частини (4) на , знаючи, що якщо оператор зрушення коштує перед константою, то він неї зберігає.

Проблема, що виникає при оцінюванні моделі розподіленого лага - це визначення величини найбільшого лага. Найпростіший спосіб: взяти модель із досить більшим лагом і перевірити гіпотези по відсіканню хвоста за допомогою t і F-Статистик.

Ar модель із розподіленим лагом

Під динамічною регресією розуміють таку регресію, у якій у якості регресорів використовуються лаги залежної змінної.

Розглянемо досить загальну модель із однієї незалежної змінної (AR модель із розподіленим лагом):

(6)

Перша сума - AR член у вигляді розподіленого лага залежної змінної.

Друга сума - розподілений лаг незалежної змінної.

ADL(p,q) - autoregressive distributed lag.

В операторної формі модель ADL(p,q) така:

(7)

де - багаточлени.

Розглянемо чистий варіант моделі: ADL(1,1):

(8)

Розглянемо найбільше що часто зустрічаються моделі, які є окремими випадками моделі ADL.

1. ADL(0,q): це модель розподіленого лага, що є ні що інше, як AR модель із розподіленим лагом порядку (0,q), тобто в правій частині немає лагів залежної змінної.

2. Модель геометрично розподіленого лага після перетворення Койко є ні що інше, як ADL(1,0) з МА(1)-помилкою й обмеженням, що коефіцієнт 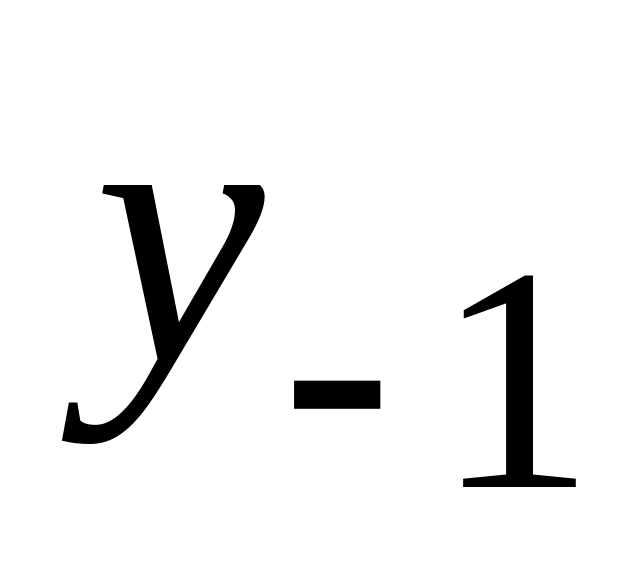дорівнює параметру МА процесу 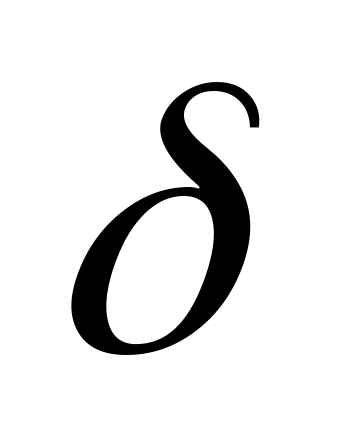зі зворотним знаком, тобто цю модель можна записати так:

3. AR модель – теж окремий випадок ADL: AR(p)=ADL(p,0) з обмеженням

У цій моделі змінна в лівій частині залежить тільки від власних лагів.

4. В економіці не завжди суб'єкти можуть пристосуватися до мінливих умов. Потрібно час на навчання, адаптацію, перехід на нові технології, на зміну умов довгострокових контрактів і т.д. ці процеси можна моделювати за допомогою так званої