8.1.3. График функции распределения

Доказанные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми  ,   (первое свойство).

При возрастании   в интервале  , в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство).

При   ординаты графика равны нулю; при   ординаты графика равны единице (третье свойство).

График функции распределения непрерывной случайной величины изображен на рис. 2.

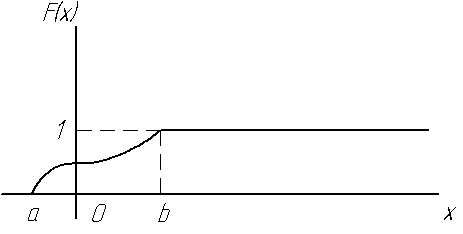
Рис. 8.1

 

Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере.

Пример 8.1. Дискретная случайная величина   задана таблицей распределения

	1	4	8
	0,3	0,1	0,6

 

Найти функцию распределения и вычертить ее график.

Решение. Если  , то   (третье свойство).

Если  , то  . Действительно,   может принять значение 1 с вероятностью 0,3.

Если  , то  . Действительно, если   удовлетворяет неравенству  , то   равно вероятности события   которое может быть осуществлено, когда   примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события   равна сумме вероятностей  .

Если  , то  . Действительно, событие   достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

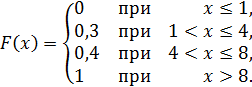
График этой функции приведен на рис. 8.2.

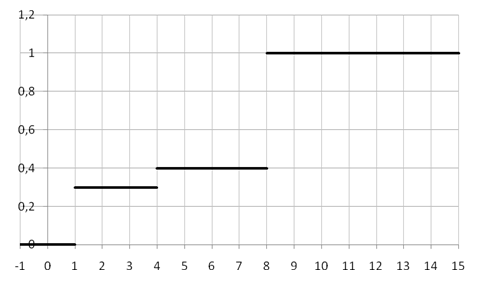
Рис. 8.2.

8.2. Плотность распределения вероятностей непрерывной случайной величины

8.2.1. Определение плотности распределения

Выше непрерывная случайная величина задавалась с помощью функции распределения. Этот способ задания не является единственным. Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют дифференциальной функцией).

Плотностью распределения вероятностей непрерывной случайной величины   называют функцию   — первую производную от функции распределения  :

Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

19.Модель процесса распространения эпидемий

Российские ученые создали математическую модель эпидемии в мегаполисе, которая не только описывает распространение заболеваемости в городе, но и подсказывает, какие меры борьбы с ней более эффективны. Об этом они написали в журнале «Математическое моделирование». Автор исследования: В.Д.Перминов; Корнилина М.А., Институт математического моделирования РАН  Есть немало математических моделей, описывающих процесс распространения инфекционных заболеваний, но они не учитывают демографическую структуру мегаполиса и, сложную систему контактов между его жителями. Новая модель, созданная совместным усилиями ученых Центрального аэрогидродинамического института (ФГУП ЦАГИ) им. Н.Е.Жуковского и Института математического моделирования РАН, - индивидуум-ориентированная. Она учитывает все. Количество жителей в городе, их пол и возраст, социальный статус и семейное положение, места работы и отдыха: насколько вместительно помещение, и все ли сегодня вышли на работу. Необходимы для модели и данные о болезни: ее длительность, варианты течения, образуется ли у переболевшего иммунитет, сделаны ли прививки, какова вероятность заражения в разных ситуациях. Например, в школе или в общественном транспорте. По сути, модель воспроизводит день за днем жизнь большого города в мельчайших подробностях. Столько-то человек заболели и остались дома, столько мамочек сидят с больными детьми, но днем сбегают в магазин, где могут заразиться сами или заразить других. Из вышедших на работу столько-то вирусоносители. Кто-то понесет свой вирус на малое предприятие, а кто-то - на крупное. Избежавший заражения днем добрый молодец пойдет вечером в кино, и есть вероятность, что там-то он и встретит своего вирусоносителя. Какое-то количество людей обратится к врачу, а другие – глотнут колдрексу – и снова в бой - заражать коллег. Все эти сложные и многочисленные контакты определяют распространение болезни. И все они учитываются в новой модели.  На основе статистических данных о Дрездене, представленных главой статистического департамента г. Дрездена доктором У. Шмидтом, и о Москве, ученые создали «модельную эпидемию». Рассмотрев ее в мельчайших подробностях, они сделали некоторые выводы.  Наиболее активное участие в распространении заболевания принимают дети – школьники и воспитанники детских садов. Причем, чем больше детей были вакцинированы, тем меньше горожан заболеет. Велико влияние семьи, которая выступает в роли инфекционного моста между различными учреждениями города.  Нарушение известного правила «заболел – сиди дома» приводит к заметному увеличению числа больных. А привычка объявлять во время эпидемии дополнительные каникулы никак не сказывается на количестве больных, она ведет только к увеличению продолжительности эпидемии. Правда, хорошо выбранное время для каникул, позволит распределить нагрузку на поликлиники более равномерно, избегая характерных для эпидемии пиков.  Имеющие отношение к эпидемиологии скажут, что это известные факты, подтвержденные медицинской статистикой. «И это замечательно, - можем воскликнуть мы, – значит, модель работает». И, убедившись в ее работоспособности, можно моделировать влияние различных противоэпидемических мер и выбирать наиболее действенную.  Все хорошо, есть только одно «но»… Для работы модели необходимы надежные демографические и статистические данные по каждому городу. 

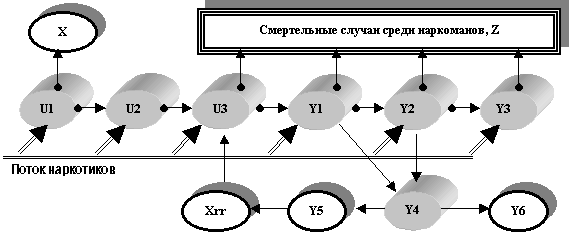
Модель наркотизации. В ядре наркоэпидемии (см. рис. 1) функционирует сложный динамический феномен, связанный с инерцией процесса наркомании у множества лиц, пораженных наркотиками. Поэтому при создании модели наркоэпидемии модель процесса наркотизации играет ведущую роль, т.к. именно эта модель представляет собой "душу" наркомании. Изучение процесса наркотизации людей, пораженных наркотиками, является ключевым моментом в понимании общих закономерностей эпидемического распространения наркомании и поиска рациональных мер борьбы с ней. Известно, что проникновение в организм человека наркотиков вызывает характерную биохимическую реакцию, т.к. в нем формируется определенное патологическое состояние, отражающее состояние наркотизма. В результате регулярного использования наркотиков в организме наркоманов возникают разнообразные патологические состояния - от гибели человека от наркотиков до наркотического опьянения. Изучение и сравнительная оценка характеристик различных форм наркотизма людей, а также обобщение этих форм наркотизма позволили нам выявить диагностически значимые симптомы наркомании и характерные состояния процесса наркотизации (см. рис. 2). При первых контактах восприимчивого индивидуума Xr (потенциальный наркоман) с наркотиками он переходит в первую латентную стадию наркомании - первоначальное состояние процесса наркотизации - U1 (проба различных наркотиков или состояние полинаркотизма). Далее, по мере нарастания интенсивности приема наркотиков, в организме формируется вторая латентная стадия U2 - процесс выбора "своего" наркотика. Эта стадия при продолжении приема наркотиков переходит в третью латентную стадию - синдром измененной реактивности - U3. Синдром измененной реактивности (U3) отражает качественно иное состояние организма, чем до приема наркотиков. Формы проявления этого синдрома и сроки его формирования весьма специфичны и строго индивидуальны, т.к. имеются существенные отличия в биохимических процессах взаимодействия наркотика и защитных систем организма каждого человека. В этом состоянии индивидуум постепенно меняет схему потребления наркотика (нарастает доза). В организме идет процесс изменения толерантности, и формируется процесс потери защитных реакций организма при передозировке наркотика на фоне изменения форм наркоопьянения. Рис. 2. Схема процесса наркотизации с учетом лечения наркоманов. X - невосприимчивые лица (группа минимального риска); U1 - лица на этапе ознакомления с наркотиками и полинаркотизма; U2 - лица на этапе выбора "своего" наркотика; U3 - лица с синдромом измененной реактивности; Y1 - лица с синдромом психической зависимости; Y2 - лица с синдромом психической и физической зависимости; Y3 - лица с синдромом хронической наркотизации (инвалиды); Xrr - восприимчивые к наркотикам (группа повторного риска); Y4 - лица на лечении в наркодиспансерах; Y6 - лица со стойкой ремиссией; Y5 - лица с нестойкой ремиссией;Z - лица, погибшие от наркотиков. Синдром психической зависимости (Y1) включает неудержимое психическое влечение индивидуума к наркотику и способность достижения состояния психического комфорта в интоксикации. Способность достижения психического комфорта в интоксикации заключается в том, что постепенно наркоман начинает осознавать, что только под действием наркотика его психическое самочувствие удовлетворительно. Наркотик становится необходимым условием благополучного психического существования организма человека. Синдром психической и физической зависимости (Y2) включает физическое (компульсивное) влечение, способность достижения физического комфорта в интоксикации и абстинентный синдром. Физическое влечение выражается в неодолимом стремлении к наркотизации; способно замещать все сознание индивидуума в данный момент, при этом вытесняются все другие влечения – жажда, голод, либидо. Физическое влечение начинает определять все поступки наркомана, мотивацию всех его действий. Синдром последствий хронической наркотизации (Y3) включает различные специфические изменения личности наркомана, вплоть до так называемого апато-абулического личностного дефекта, слабоумия при некоторых формах наркоманий. Происходит психологическая инвалидизация, падает психическая активность, ограничивается интеллект и мотивационная сфера, упрощаются побуждения, обедняется эмоциональная гамма, происходит нравственно-этическая деградация, резко снижается социальное функционирование, которое заканчивается смертью больного. Лечение наркомании включает в себя различные курсы, которые могут иметь для наркоманов в стадиях Y1, Y2, Y3 следующие исходы: переход в новое патологическое состояние, связанное с ремиссией Y5 и с последующим переходом в группу Xrr; переход в состояние, связанное с устойчивой ремиссией Y6 и полным отказом от употребления наркотиков. Рассмотренные здесь стадии наркотизации были использованы для количественного описания процессов развития наркоэпидемии в виде соответствующих балансовых уравнений для "потоков" индивидуумов (см. рис. 2). Система уравнений математической модели наркоэпидемии была реализована в виде компьютерной программы, которая позволила провести расчетные исследования по анализу и прогнозу наркоэпидемии на территории России. 4. Прогноз наркоэпидемии в России до 2005 года Объектом исследования была наркоэпидемия в целом для России, которая отражает общенациональные проблемы наркомании - ее масштабы и интенсивность развития. При создании прогностической модели мы исходили из того, что условия для "старта" наркоэпидемии сформировались в России к концу 1991 года. После этого в стране начался подъем наркомании и рост численности наркоманов, а также рост "емкости" российского наркорынка. Для выявления общих закономерностей развития наркомании и верификации компьютерной модели наркоэпидемии были использованы статистические данные, представленные в таблице 4.

 

20. Модель колебательных процессов в физике

Колебательные и волновые процессы изучают в одном разделе. Этим подчеркивается огромная роль учения о колебаниях в современной науке и технике и то общее, что присуще этим движениям независимо от их природы. Колебательным и волновым процессам присущи некоторые характерные закономерности, общие для колебаний различной физической природы. Иначе говоря, характер поведения характеристических кривых колебательных и волновых процессовидентичен характеру поведения кривых соответствующих векторных диаграмм. Бесконечно протяженные характеристические кривые характерны для моделей, описывающих диффузионные процессы, а конечно протяженные кривые характерны для моделей, описывающих волновые процессы. Во втором томе Основ физики рассмотрены: колебательные и волновые процессы, включая оптику, современные представления о физике атомов, молекул, твердых тел и об их важнейших свойствах. Все разделы второго тома, так же как и первого, органически связаны с теорией относительности и квантовой механикой. От читателя требуется основательное знание математики и физики в объеме неполной средней школы. Работа над книгой поможет школьникам изучить курс физики достаточно углубленно и на современном уровне. [4]

Статистическая радиофизика занимается изучением стохастических явлений в колебательных и волновых процессах. В математическом плане дело сводится к решению линейных или нелинейных дифференциальных уравнений со случайными начальными ( или краевыми) условиями, случайными параметрами ( коэффициентами), случайными внешними силами - так называемых стохастических дифференциальных уравнений. [5]

Во многих практически важных ситуациях наиболее адекватным описанием колебательных и волновых процессов оказывается статистическое описание; так, в радиофизике и оптике, наряду с регулярными, появляются случайные колебания и волны. Статистика в радиофизику и оптику приходит потому, что многие источники радио - и световых колебаний представляют собой, по существу, генераторы шума. Хаотически изменяются параметры систем, свойства сред, в которых распространяются радио - и световые волны. Особое место в радиофизике и оптике занимают задачи, связанные с эффектами электромагнитных флуктуации материальной среды. Собственные электромагнитные флуктуации ставят флуктуацион-ный предел чувствительности приемников, точности измерений, оказываются причиной принципиальной невозможности генерирования строго монохроматических колебаний. 

В книге изложены основы теории статистических явлений в колебательных и волновых процессах. В отличие от традиционных курсов статистической радиофизики, в предлагаемой книге большое внимание уделено задачам статистической оптики. Значительное внимание уделено новым теоретическим методам статистической радиофизики и оптн-ки. Ряд разделов книги иллюстрируется экспериментальными данными. В наши задачи не может также входить систематический анализ многочисленных колебательных и волновых процессов, возникающих в плазме. Слишком обширен и сложен материал, и мы ограничимся главным. 

В данной работе на основе асимптотических формул и предельных значений характеристических величинколебательных и волновых процессов проводится сравнительный анализ динамического поведения материалов, свойства которых описываются реологическими моделями ( 4) - ( 7), а также устанавливается аналогия в поведении реологических и динамических характеристиках перечисленных моделей. В более широком смысле под статистической радиофизикой понимают круг задач, связанных с изучением статистических явлений в колебательных и волновых процессах, причем речь не обязательно идет об электромагнитных колебаниях и волнах. В книге дано краткое изложение основных разделов школьного курса физики: механики, молекулярной физики, электродинамики, колебательных и волновых процессов, квантовой физики. Книга призвана оказать помощь с систематизаци; и обобщении знаний по курсу физики VII-XI классов, что нашло твое отражение в ее содержании и структуре. Начиная с изучения ньютоновской механики и теории относительности, мы последовательно рассмотрели основы термодинамики и молекулярной физики, электродинамику, колебательные и волновые процессы, включая учение об электромагнитных волнах и оптику. При этом мы стремились показать, что идеи специальной теории относительности пронизывают всю современную физику и позволяют по-новому осветить многие разделы классической физики. С самого начала курса мы стремились показать, что в атомном мире существуют определенные ограничения для чисто классического описания микрообъектов. В - данном разделе курса физики изучаются механические, звуковые, ультразвуковые и электромагнитные колебания и волны и устанавливаются общие закономерности, присущие колебательным и волновым процессам любой природы. Класс рассмотренных реакций интересен не только тем, что он представляет собой нетривиальное химическое явление, но и тем, что он служит удобной моделью для изучения колебательных и волновых процессов в активных средах. Сюда относятся периодические процессы клеточного метаболизма; волны активности в сердечной ткани и ткани мозга; процессы, происходящие на уровне экологических систем.