18.Розыгрыш дискретной случайной величины
Вспомним, что дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Такой способ задания не является общим: он неприменим, например, для непрерывных случайных величин.
Действительно,
рассмотрим случайную величину 
,
возможные значения которой сплошь
заполняют интервал 
.
Можно ли составить перечень всех
возможных значений
?
Очевидно, что этого сделать нельзя. Этот
пример указывает на целесообразность
дать общий способ задания любых типов
случайных величин. С этой целью и вводят
функции распределения вероятностей
случайной величины.
Пусть 
—
действительное число. Вероятность
события, состоящего в том, что
примет
значение, меньшее
,
т.е. вероятность события 
,
обозначим через 
.
Разумеется, если
изменяется,
то, вообще говоря, изменяется и
,
т.е.
—
функция от
.
Функцией распределения называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее , т.е.
Геометрически это равенство можно истолковать так: есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки .
Иногда вместо термина «функция распределения» используют термин «интегральная функция».
Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называютнепрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
8.1.2. Свойства функции распределения
Свойство
1. Значения
функции распределения принадлежат
отрезку 
:
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
Свойство
2. 
—неубывающая
функция, т.е.
, если 
Доказательство.
Пусть 
.
Событие, состоящее в том, что
примет
значение, меньшее 
,
можно подразделить на следующие два
несовместных события: 1)
примет
значение, меньшее 
,
с вероятностью 
;
2)
примет
значение, удовлетворяющее неравенству 
,
с вероятностью 
.
По теореме сложения имеем
Отсюда
или
|
(8.1) |
Так
как любая вероятность есть число
неотрицательное, то 
,
или
,
что и требовалось доказать.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения на этом интервале:
|
(8.2) |
Это
важное следствие вытекает из формулы
(8.1), если положить 
и 
.
Пример 8.1. Случайная величина задана функцией распределения
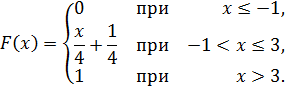
Найти
вероятность того, что в результате
испытания
примет
значение, принадлежащее интервалу 
Решение.
Так как на интервале 
,
по условию,
то
Итак,
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
Действительно,
положив в формуле (8.2) 
,
имеем
Устремим 
к
нулю. Так как
—
непрерывная случайная величина, то
функция
непрерывна.
В силу непрерывности
в
точке
разность 
также
стремится к нулю; следовательно, 
Используя
это положение, легко убедиться в
справедливости равенств
|
(8.3) |
Например,
равенство 
доказывается
так:
Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.
Заметим,
что было бы неправильным думать, что
равенство нулю вероятности 
означает,
что событие 
невозможно
(если, конечно, не ограничиваться
классическим определением вероятности).
Действительно, в результате испытания
случайная величина обязательно примет
одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство
3. Если
возможные значения случайной величины
принадлежат интервалу
,
то: 1) 
при 
;
2) 
при 
.
Доказательство.
1)
Пусть 
.
Тогда событие 
невозможно
(так как значений, меньших
величина
по
условию не принимает) и, следовательно,
вероятность его равна нулю.
2)
Пусть 
.
Тогда событие 
достоверно
(так как все возможные значения
меньше
)
и, следовательно, вероятность его равна
единице.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси , то справедливы следующие предельные соотношения:
