14. Метод Рунге-Кутта решения дифференциальных уравнений

Ме́тоды Ру́нге — Ку́тты (распространено неправильное название Ме́тоды Ру́нге — Ку́тта или даже Ме́тоды Ру́нге — Кутта́) — важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Методы седьмого порядка должны иметь по меньшей мере девять стадий, в схему восьмого порядка входит 11 стадий. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько стадий необходимо для достижения этого порядка точности. Аналогичная задача существует для схем десятого и более высоких порядков

Классический метод Рунге — Кутты четвёртого порядка

Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Рассмотрим задачу Коши

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

Вычисление нового значения проходит в четыре стадии:

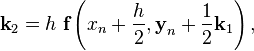
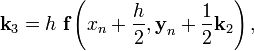
где   — величина шага сетки по  .

Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок   (ошибка на каждом шаге порядка  ).

Прямые методы Рунге — Кутты[править | править исходный текст]

Семейство прямых методов Рунге — Кутты является обобщением метода Рунге — Кутты четвёртого порядка. Оно задаётся формулами

где   — величина шага сетки по   и вычисление нового значения проходит в   этапов:

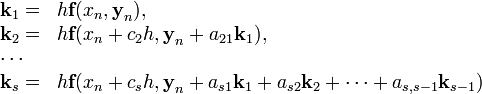
Конкретный метод определяется числом   и коэффициентами   и  . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Бутчера)

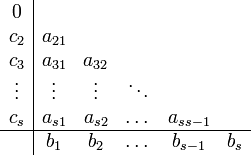
Для коэффициентов метода Рунге — Кутты должны быть выполнены услови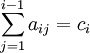я   для  . Если требуется, чтобы метод имел порядок  , то следует также обеспечить условие

где   — приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.

15. Движение тела, брошенного под углом к горизонту

Теория

Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения  ; проекции ускорения на координатные оси равны а_х = 0, а_у = -g.

Л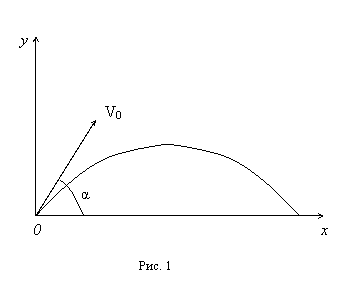 юбое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).

Проекции скорости тела, следовательно, изменяются со временем следующим образом:

,

где   – начальная скорость, α – угол бросания.

Координаты тела, следовательно, изменяются так:

При нашем выборе начала координат начальные координаты   (рис. 1) Тогда

(1)

Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета: 

.

(2)

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.

Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t₀. Подставляя значение (2) в первую формулу (1), получаем:

.

(3)

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.

Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

.

(4)

Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:

и подставить его во второе уравнение. Тогда получим:

.

Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.