5.Численный Эксперемент

6. Задачи линейного програмирования.Примеры

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах  -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

В 1938 году Леонид Витальевич Канторович в порядке научной консультации приступил к изучению чисто практической задачи по составлению наилучшего плана загрузки лущильных станков (фанерный трест). Эта задача не поддавалась обычным методам. Стало ясно, что задача не случайная.^[1]

В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования.

Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида^[3]:

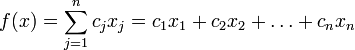
Задача, в которой фигурируют ограничения в форме неравенств, называется основной задачей линейного программирования (ОЗЛП)

,

.

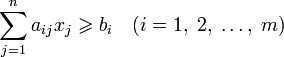Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства^[4]:

,

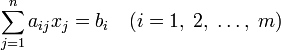Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств^[5].

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты   с обратным знаком.

7. Транспортная модель линейного программирования

8. Многоотраслевая модель экономики Леонтьева

 Каждая отрасль многоотраслевого хозяйства с одной стороны является производите-лем определенной продукции, а с другой – потребителем продукции, выпускаемой другими отраслями. Макроэкономика функционирования многоотраслевого хозяйства требует, чтобы соблюдался баланс по производству и потреблению между отдельными отраслями. Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск i-й отрасли должен быть равен сумме объемов потребления. В простейшей форме балансовые соотношения имеют вид x_i=x_i1 + x_i2 + … + x_in + y_i , i=1, 2, …, n. где x_i – общий объем выпускаемой продукции i–й отрасли; x_ij – объем продукции i–й отрасли, потребляемый j –й отраслью при производстве объема продукции x_j; y_i – объем продукции i–й отрасли конечного потребления (для реализации а непро-изводственной сфере). Для производства продукции j –й отрасли объемом xi нужно использовать продукцию i –й отрасли объемом a_ijx_i , где а_ij – постоянное число, характеризующее прямые затраты. Это допущение позволяет представить модель многоотраслевой экономики в виде системы линейных уравнений, которая в матричной форме имеет вид   ,

где  x- вектор валового выпуска;

       y- вектор объема продукции конечного потребления;

    A - матрица коэффициентов прямых затрат. Приведенная система уравнений может быть представлена в виде  , где E – единичная матрица. Если существует обратная матрица   (матрица полных затрат), то существует единственное решение системы   . Из экономической теории известно несколько критериев продуктивности матрицы А:

1) матрица А продуктивна тогда и только тогда, когда матрица   существует и ее элементы неотрицательны;

2) матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не больше единицы, при чем хотя бы для одного столбца (строки) строго меньше единицы.

Рассмотрим пример решения задачи на применение модели Леонтьева.

Пример 7. В таблице приведены данные по балансу за некоторый период времени между пятью отраслями.

№	Отрасль	Потребление					Конечный продукт	Валовой выпуск (ден.ед)
		1	2	3	4	5
1	Станкостроение	15	12	24	23	16	10	100
2	Энергетика	10	3	35	15	7	30	100
3	Машиностроение	10	5	10	10	10	5	50
4	Автомобильная промышленность	10	5	10	5	5	15	50
5	Добыча и переработка углеводородов	7	15	15	3	3	50	100

Требуется найти векторы конечного потребления и валового выпуска, а также матрицу коэффициентов прямых затрат и определить ее продуктивность.

Решение:1. В диапазон ячеек рабочего листа (B3:F7) введите числа, записанные в столбцах “Потребление” исходной таблицы.2. Введите в диапазон ячеек (H3:H7) значения вектора X, который соответствует последнему столбцу исходной таблицы (см. рис.8).3. Введите в диапазон (I3:I7) значения вектора Y - вектор конечного продукта.4. Матрица прямых затрат А вычисляется путем деления i – того столбца матрицы “Потребление” на i – ую строку вектора Х. Это вычисление можно выполнить используя формулу А= П/Хт, где П – матрица “Потребление”.5. Выделите диапазон ячеек, в котором будет размещаться матрица А и введите в него формулу деления массива “Потребление” на транспонированный “Вектор Х ”: = B3:F7/ТРАНСП(H3:H7) (см рис.) и нажмите комбинацию клавиш Ctrl + Shift + Enter. После выполнения этой операции в выделенном диапазоне будут вычислены значения элементов матрицы А.6. Просуммируйте столбцы полученной матрицы, используя автосуммирование. Значения элементов полученной матрицы положительные, следовательно, первый критерий продуктивности матрицы выполняется. Однако значения сумм в третьем и четвер-том столбцах больше единицы, следовательно, второй критерий продуктивности не выполня-ется. Таким образом, матрица полных затрат для условий рассматриваемой задачи является не продуктивной.