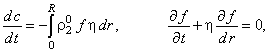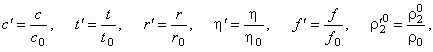23. Обезразмеривание системы уравнений

Значения параметров, получаемые с помощью методов численного решения дифференциальных уравнений, как правило несколько отличаются от их истинных значений из-за наличия ошибки аппроксимации. Поэтому алгоритмы решения уравнений математических моделей, изучаемые в данном пособии, могут оказаться непригодными, если уравнения модели содержат переменные, значения которых отличаются по порядкам. Так, погрешности при определении параметров, порядки которых велики, могут быть не значимы для них самих, но в то же время они будут сильно искажать значения параметров меньших порядков. Поэтому прежде чем перейти к созданию алгоритма для решения уравнений математической модели, необходимо привести эти уравнения к безразмерному виду, т.е. провести операцию обезразмеривания переменных, в результате которой все переменные математической модели будут иметь одинаковый порядок.       Рассмотрим процедуру обезразмеривания на примере математической модели процесса кристаллизации, протекающего в ёмкостном периодическом реакторе идеального смешения:

(2.1)

где с - объёмная концентрация кристаллизующегося компонента;   - плотность кристалла;   - скорость роста кристалла;   - число кристаллов в единице объёма смеси с размером от r до r + dr; R - наибольший размер кристалла.       Безразмерные переменные вводятся с помощью соотношений:

где переменные с индексом (0) соответствуют характерным параметрам процесса.       Как правило, могут быть известны лишь некоторые характерные параметры процесса, например, в данном случае это характерное время процесса (t₀), характерный размер кристалла (r₀) и характерная концентрация кристаллизующегося компонента в растворе (с₀). Кроме этого, обычно принимают равенство:

поскольку в модели (2.1) плотность и концентрация имеют одинаковую размерность. Однако характерную скорость роста кристаллов ( ) и характерное значение плотности функции распределения кристаллов по размерам ( ) непосредственно измерить невозможно. Их значения определяют из безразмерных комплексов характерных параметров согласно методике

24. Движение заряженных частиц в электростатическом поле точечных источнико

На заряженную частицу в электростатическом поле действует кулоновская сила, которую можно найти, зная напряженность поля в данной точке

Эта сила сообщает ускорение

где m — масса заряженной частицы. Как видно, направление ускорения будет совпадать с направлением  , если заряд частицы положителен (q > 0), и будет противоположно  , если заряд отрицателен (q<0).

Если электростатическое поле однородное (  = const), то ускорение   = const и частица будет совершать равноускоренное движение (разумеется, при отсутствии других сил). Вид траектории частицы зависит от начальных условий. Если вначале заряженная частица покоилась   или ее начальная скорость сонаправлена с ускорением  , то частица будет совершать равноускоренное прямолинейное движение вдоль поля и ее скорость будет расти. Если  , то частица будет тормозиться в этом поле.

Если угол между начальной скоростью и ускорением острый О <   < 90° (или тупой), то заряженная частица в таком электростатическом поле будет двигаться по параболе.

Во всех случаях при движении заряженной частицы в электростатическом поле будет изменяться модуль скорости, а следовательно, и кинетическая энергия частицы.

Существенное отличие магнитного поля от электростатического состоит, во-первых, в том, что магнитное поле не действует на покоящуюся заряженную частицу. Магнитное поле действует только на движущиеся в поле заряженные частицы. Во-вторых, сила Лоренца, действующая на заряженные частицы в магнитном поле, всегда перпендикулярна скорости их движения. Поэтому модуль скорости в магнитном поле не изменяется. Не изменяется, следовательно, и кинетическая энергия частицы. Вид траектории заряженной частицы в магнитном поле зависит от угла между скоростью влетающей в поле частицы и магнитной индукцией. Возможны три различных случая.

1. Заряженная частица влетает в магнитное поле со скоростью 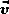 , направленной вдоль поля 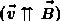  или противоположно направлению магнитной индукции поля  . В этих случаях сила Лоренна 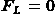  и частица будет продолжать двигаться равномерно прямолинейно.

2. Заряженная частица движется перпендикулярно линиям магнитной индукции (рис. 1), тогда сила Лоренца 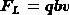 , а следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы. В результате частица будет двигаться по окружности, радиус которой можно найти на основании второго закона Ньютона:

Отношение   — называют удельным зарядом частицы.

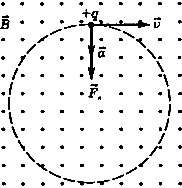
Рис. 1

Период вращения частицы

то есть период вращения не зависит от скорости частицы и радиуса траектории. На этом основано действие циклотрона.

3. Скорость заряженной частицы направлена под углом   к вектору 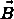  (рис. 2).

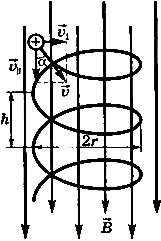
Рис. 2

Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью   и движения по окружности с постоянной по модулю скоростью   в плоскости, перпендикулярной полю. Радиус окружности определяется аналогично предыдущему случаю, только надо заменить   на  , то есть

В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол   с направлением вектора  неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то R и h уменьшаются с ростом B. На этом основана фокусировка заряженных частиц в магнитном поле.

Если на движущуюся заряженную частицу помимо магнитного поля с индукцией  действует одновременно и электростатическое поле с напряженностью  , то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы Лоренца

Характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.