МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Дальневосточный федеральный университет»

(ДВФУ)

ШКОЛА ЕСТЕСТВЕННЫХ НАУК ДВФУ

Исследование затухающих колебаний в колебательном контуре Лабораторная работа № 3. 57 Учебно-методическое пособие

Владивосток 2012

3. 57 Исследование затухающих колебаний в колебательном контуре

Цель работы: изучение процессов в колебательном контуре, возникающих при его возбуждении, исследование влияния параметров контура на протекание этих процессов.

Оборудование: Осциллограф со встроенным генератором импульсов, магазин емкости, магазин индуктивности, магазин сопротивления, провода.

Теория метода

Колебательным контуром называют систему, состоящую из катушки с индуктивностью L, конденсатора электроемкостью С и омического сопротивления R, обусловленного обмоткой катушки и подводящих проводов. Если сопротивлением катушки и проводов можно пренебречь, то такой контур называется идеальным.

Рассмотрим процессы, возникающие в реальном электрическом колебательном контуре, см. рисунок 1. Изображенная на рис. 1 схема называется схемой с сосредоточенными параметрами. Омическое сопротивление катушки и проводов эквивалентно сопротивлению резистора R, включенного последовательно с конденсатором и катушкой, при этом катушка обладает только индуктивностью L.

Р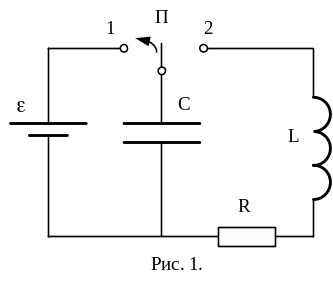 ассмотрим вначале процессы, протекающие в контуре качественно. Для возбуждения в контуре колебаний конденсатор предварительно заряжают от источника постоянного тока ε, поставив ключ П в положение 1, сообщая его обкладкам заряд q. Тогда в начальный момент времени t = 0 между обкладками конденсатора возникнет электрическое поле, энергия которого равна . При замыкании конденсатора на катушку индуктивности (ключ в положении 2) он начинает разряжаться, и в контуре потечёт возрастающий со временем ток, который будет создавать внутри катушки нарастающее магнитное поле. При этом в катушке возникает ЭДС самоиндукции ε, пропорциональная скорости изменения тока:

. (1)

Согласно правилу Ленца ЭДС самоиндукции противодействует нарастанию тока и, следовательно, замедляет разряд конденсатора. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки возрастать. В момент времени t = Т/4 энергия электрического поля обращается в нуль, а ток I и энергия магнитного поля W достигают наибольшего значения: .

Начиная с этого момента, ток в контуре будет убывать, а, следовательно, начнет ослабевать магнитное поле катушки. Это снова вызовет появление ЭДС самоиндукции, но на этот раз направленной на поддержание магнитного поля и, следовательно, в катушке индуцируется ток, направленный в ту же сторону, что и первоначальный ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле стремящееся ослабить ток, который, в конце концов, обратится в нуль. Заряд на пластинах конденсатора, а, следовательно, и энергия электрического поля к моменту t = Т/2 достигнут максимума. Далее те же процессы начнут протекать в обратном направлении, и система к моменту t = T придет в первоначальное состояние. После этого начнется повторение рассмотренного цикла разрядки.

Происходящие при этом процессы изменения заряда на конденсаторе, напряжения между обкладками конденсатора, напряженности электрического и магнитного полей и называются электромагнитными колебаниями. Вследствие необратимых потерь энергии, связанных с преобразованием электромагнитной энергии во внутреннюю на сопротивлении R, эти колебания протекают конечное время.

Рассмотрим далее процесс электромагнитных колебаний количественно. Так как заряд, напряжение между пластинами и др. величины со временем изменяются непрерывно, то для установления закона изменения их со временем следует составить дифференциальное уравнение. Для составления этого уравнения воспользуемся вторым правилом Кирхгофа для цепей постоянного тока, но в данном случае, записанном для мгновенных значений токов, ЭДС и напряжений

Согласно второму правилу Кирхгофа падение напряжения на обкладках конденсатора и активном сопротивлении равно ЭДС, действующей в контуре:

. (2)

Так как , то с учетом (1) уравнение (2) примет вид:

. (3)

Поделив обе части уравнения (3) на L и учитывая, что получим:

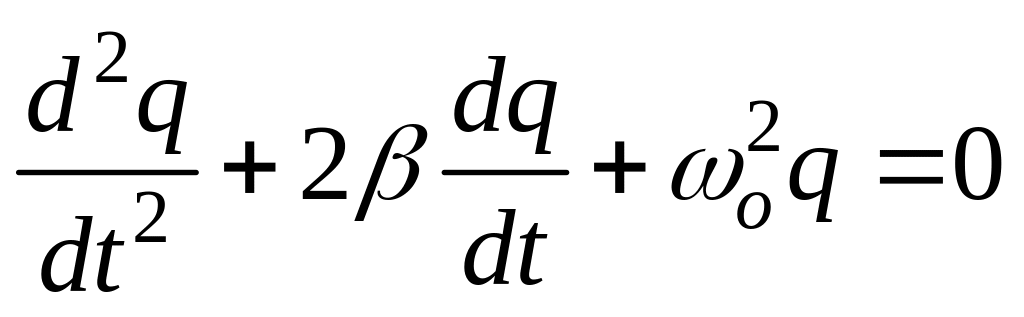, (4)

где введены обозначения:

, . (5)

Уравнение (4) и есть искомое дифференциальное уравнение свободных электромагнитных колебаний при наличии сопротивления. Решение уравнения (4) имеет вид:

, (6)

где q_o – начальная амплитуда колебаний заряда конденсатора, ω – циклическая частота затухающих колебаний, φ_o – начальная фаза.

, (7)

– коэффициент затухания. Более подробное решение показывает, что ω определяется выражением:

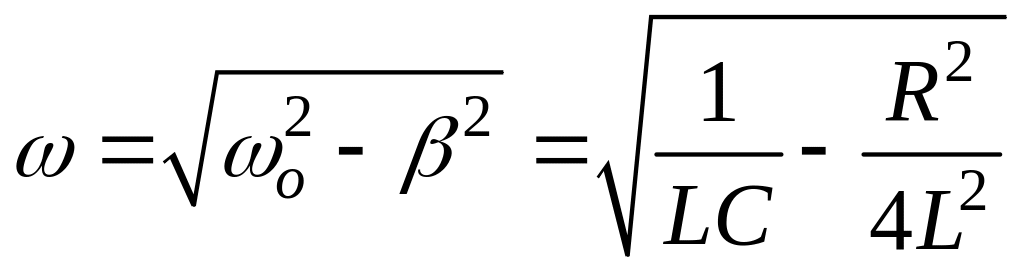, (8)

где ω и ω_о – соответственно циклическая частота колебаний при наличии сопротивления контура и без сопротивления. Циклическая частота – это число колебаний за 2π секунд. Из формулы (8) видно, что наличие сопротивления R в контуре уменьшает частоту колебаний в сравнении с частотой колебания идеального контура.

Так как , то из формулы (6) следует зависимость напряжения на конденсаторе от времени в виде:

. (9)

В уравнениях (6) и (9) выражения и соответственно играют роль амплитуд колебаний заряда и напряжения на конденсаторе колебательного контура. Например, для напряжения амплитуда равна:

(10)

Г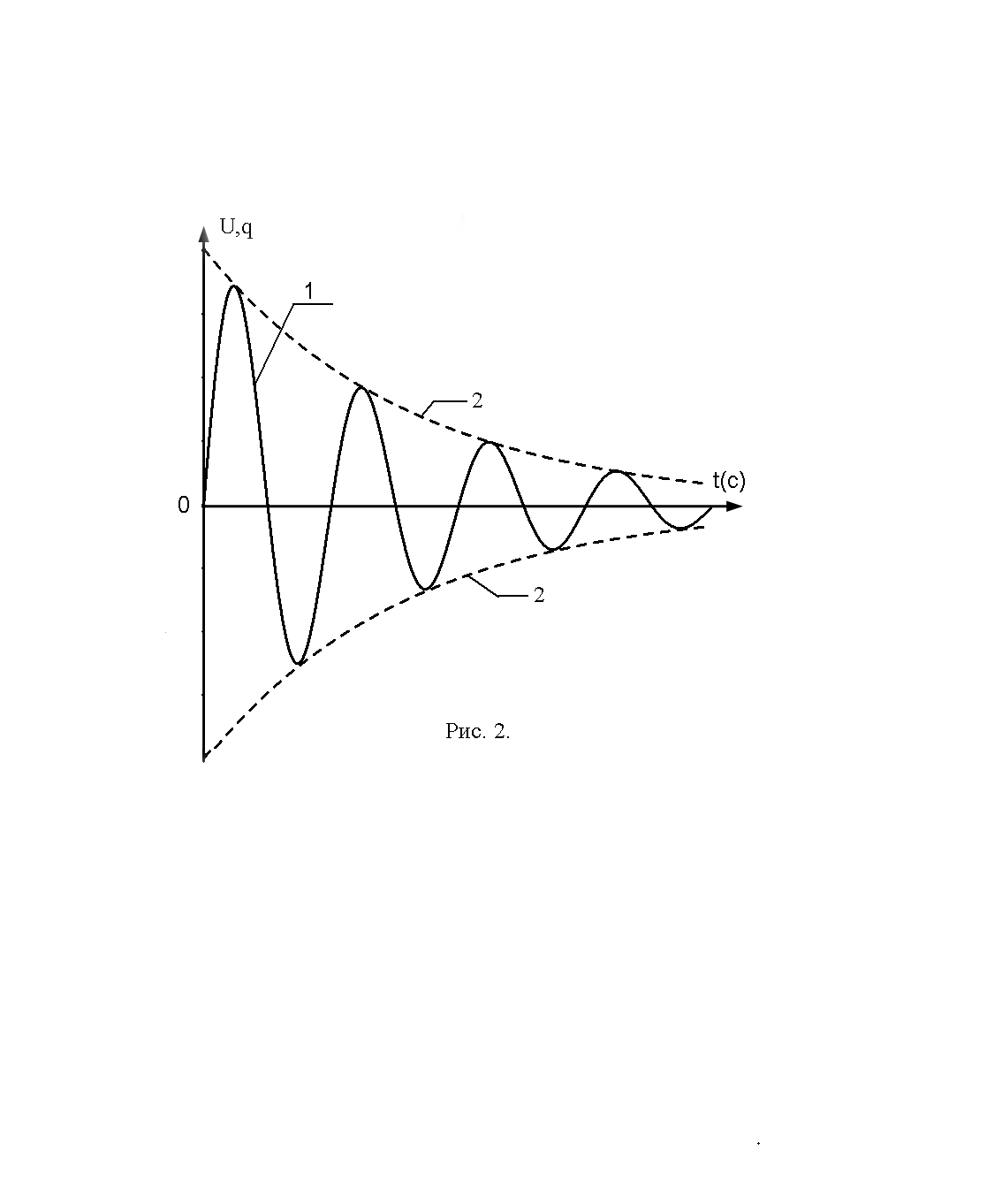 рафики выражений (6) и (9) представлены на рис. 2, кривая 1, пунктирной линией 2 показана зависимость амплитуды напряжения и заряда на конденсаторе в относительных единицах. Как видно из этих графиков, амплитуда колебаний напряжения и заряда на конденсаторе убывают, следовательно, убывает и энергия контура, что связано с джоулевыми потерями энергии на сопротивлении.

Из определения циклической частоты для затухающих колебаний, формула (8), можно рассчитать величину . Как известно из теории гармонических колебаний, она имеет смысл периода Т. В нашем случае эта величина будет определяться выражением:

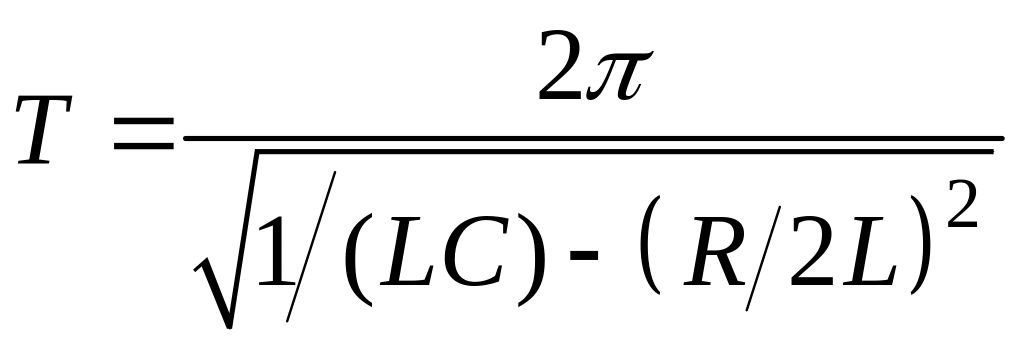. (11)

При записи формулы (11) мы учли выражение (8). Для затухающих колебаний введенное понятие периода Т является условным, так функция U(t), как видно из графика 1 (рис. 2), не является периодической. Использование этого понятия в данном случае можно частично оправдать двумя факторами: 1) расстояние вдоль оси времени между двумя соответствующими точками, определяемое формулой (10) остается постоянным: 2) при малых значениях R функция U(t), см. уравнение (9), мало отличается от гармонической, т.к. экспоненциальный множитель при этом близок к 1. В предельном случае при R = 0 функция U(t) будет строго гармонической. Таким образом, понятие периода для затухающих колебаний в определенной степени оправдано для контуров с малым сопротивлением R, т.е. малым коэффициентом затухания .

Из формулы (11) видно, что при увеличении сопротивления контура R при постоянных значениях L и C, возможна ситуация, при которой подкоренное выражение может стать равным 0, это будет означать, что период колебания Т → ∞, т.е. процесс разрядки конденсатора не будет носить колебательный характер. Такой процесс называют апериодическим. Сопротивление R, при котором имеет место апериодический характер разряда конденсатора в колебательном контуре, называют критическим сопротивлением R_кр. Его можно определить, приравняв 0 подкоренное выражение в формуле (11), тогда получим:

. (12)

При R < R_кр. Разряд конденсатора носит колебательный характер, если R ≥ R_кр., то разряд конденсатора будет апериодическим.

Для затухающих колебаний, протекающих в колебательном контуре кроме введенных выше характеристик колебаний – циклической частоты ω, периода Т и критического сопротивления R_кр. введем еще три характеристики: время релаксации τ, логарифмический декремент затухания λ, добротность Q.

Временем релаксации τ называют промежуток времени, в течение, которого амплитуда колебаний уменьшается в е раз, е – основание натуральных логарифмов, е ≈ 2,718.

Из этого определения и выражения для амплитуды колебания, например напряжения , следует связь между коэффициентом затухания β и временем релаксации τ:

или . (13)

Следовательно, коэффициента затухания β – это физическая величина, обратная времени, по истечении которого амплитуда уменьшается в е раз.

Дадим определение логарифмического декремента затухания λ и добротности колебательной системы Q, а также приведем их связь с параметрами колебательного контура.

Логарифмическим декрементом затухания λ называют физическую величину, равную натуральному логарифму отношения двух последовательных амплитуд колебания, разделенных промежутком времени в один период:

. (14)

Для уменьшения погрешностей в определение λ можно брать отношение амплитуд, разделенных целым числом периодов n. В этом случае формула для определения логарифмического декремента затухания примет вид:

(15)

Используя данное определение и формулу (10) получим связь λ с другими характеристиками затухающих колебаний и параметрами контура:

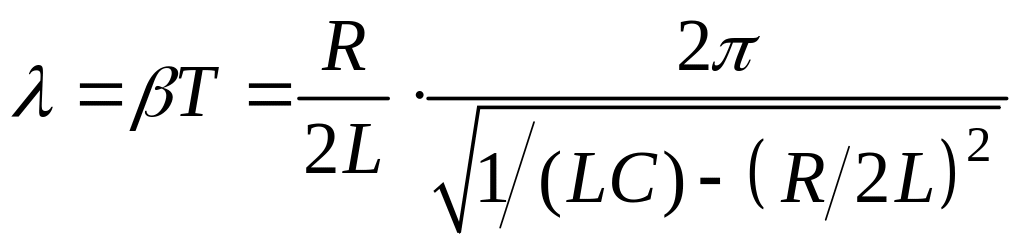. (16)

Добротность колебательной системы характеризует потери энергии запасенной контуром. Добротностью контура Q называют физическую величину показывающую, во сколько раз запас энергии контура W превосходит среднюю потерю энергии ΔW за время, в течение которого фаза колебаний изменяется на 1 радиан:

. (17)

Расчет, проведенный на основе этой формулы в предположении, что затухание колебаний невелико (ω_o >> β, при этом ω_o ≈ ω) дает для добротности выражения (см. например [3, с.290 – 291; 2, с. 310]):

; (18)

; (19)

. (20)

Формула (18) в данной работе служит для экспериментального определения добротности, формула (19) позволяет дать новую трактовку добротности колебательной системы: добротность – величина, пропорциональная числу колебаний, по истечении которых амплитуда уменьшается в е раз. Формула (20) служит для теоретической оценки добротности по известным параметрам колебательного контура. Из всех этих формул также видно, что для идеального контура (R = 0) добротность равна ∞.