Средняя гармоническая (простая и взвешенная)

Средняя гармоническая представляет собой величину обратную средней арифметической из обратных значений признака и применяется в тех случаях, когда не известен знаменатель логической формулы среднего показателя.

средняя гармоническая простая

Например:

Фирма	Фактическая реализация продукции, млн. руб. (М)	Выполнение плана по реализации продукции, % (f)
1	6,0	106
2	8,0	103
	14,0

Определить средний процент выполнения плана по двум фирмам.

%	=	факт	- это логическая формула среднего показателя
		план

средняя гармоническая взвешенная М= х*f

Средняя геометрическая и средняя хронологическая используются в рядах динамики для расчета среднегодовых темпов роста и среднего уровня.

Структурные средние (мода и медиана).

Модой (М_о) в статистике называется наиболее часто повторяющееся значение признака. Медианой (М_е) называется значение признака, приходящееся на середину упорядоченной совокупности. Мода и медиана могут быть рассчитаны для дискретных и интервальных рядов распределения.

Например:

Возраст студента,х	17	18	19	20	21
Число студентов, f	10	20	40	30	15

М_о=19 лет

М_е=19 лет

Показатели вариации

Вариация – изменение количественных значений признака. В статистике различают следующие показатели вариации:

1. размах вариации (R) рассчитывается как разность между максимальным и минимальным значениями признака.

R=х_max - х_min

2. линейное отклонение (d): представляет собой разность между значениями признака и средней величиной в изучаемой совокупности.

3. среднее линейное отклонение (đ):

а) среднее линейное отклонение простое

б) - среднее линейное отклонение взвешенное

4. дисперсия (σ²)

а) простая б) взвешенная

5. среднее квадратическое отклонение (σ):

а) - простое

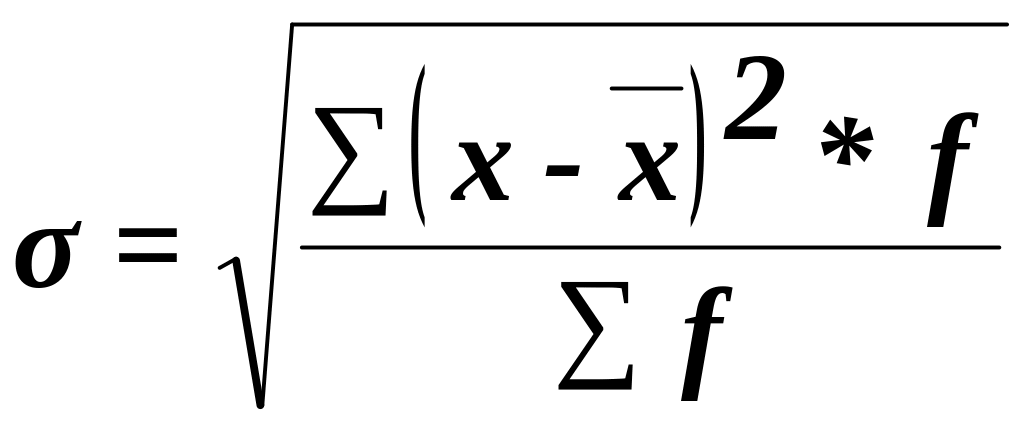б) -среднее квадратическое отклонение взвешенное

В среднем квадратическом отклонении учитываются только положительные значения. Оно выражается в тех же единицах измерения что и признак.

6. коэффициент вариации (ν)

По величине коэффициента вариации < 33% судят об однородности изучаемой совокупности, и он применяется для характеристики вариации признака каких-либо двух совокупностей.

Все показатели вариации именованные и имеют ту же размерность, что и значения признака.

Все показатели вариации подразделяются на абсолютные и относительные.

К абсолютным показателям вариации относятся:

• размах вариации;

• среднее линейное отклонение;

• среднее квадратическое отклонение.

К относительным показателям вариации относится коэффициент вариации.