Тема «Средние величины и показатели вариации» (задачи № 2, № 3)

Средние величины и показатели вариации имеют в статистике важное значение. Они широко применяются для характеристики статистических совокупностей по варьирующим признакам.

В задаче № 3 контрольной работы даются так называемые открытые интервалы, то есть, интервалы, у которых верхняя или нижняя границы точно не определены, а сама граница остается как бы открытой. В этом случае за величину открытого интервала условно принимается величина смежного закрытого интервала. Например, дан вариационный ряд распределения работников магазина:

Группы работников по величине заработка (руб. в месяц)	Число работающих (чел.)
до8000	6
от 8000 до 9000	10
от 9000 до 10000	14
и т.д.

Для определения среднего заработка величина первого (открытого) интервального варианта (если нет индивидуальных данных) принимается также равной 1000 руб.

При определении среднего квадратического отклонения при достаточно большом объеме изучаемой совокупности (n30) применяются формулы:

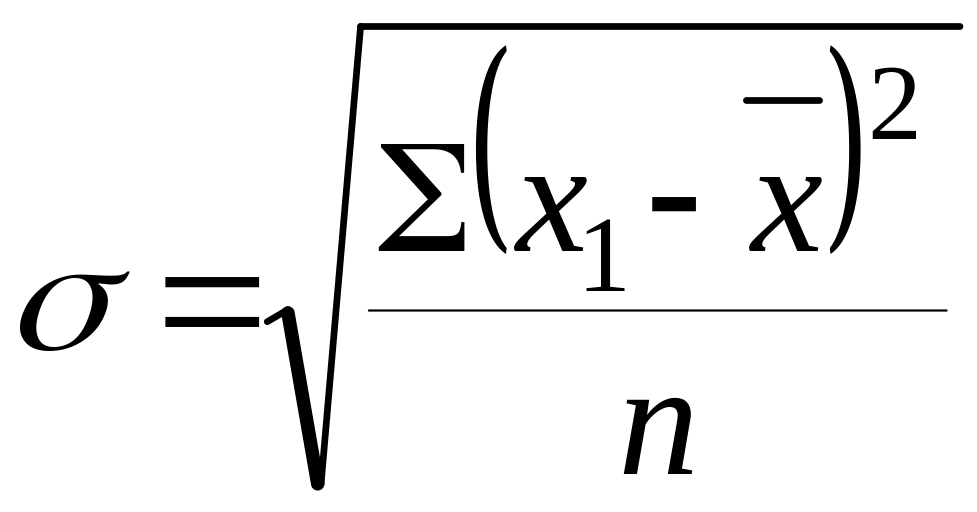(2) – среднее квадратическое отклонение простое (или невзвешенное);

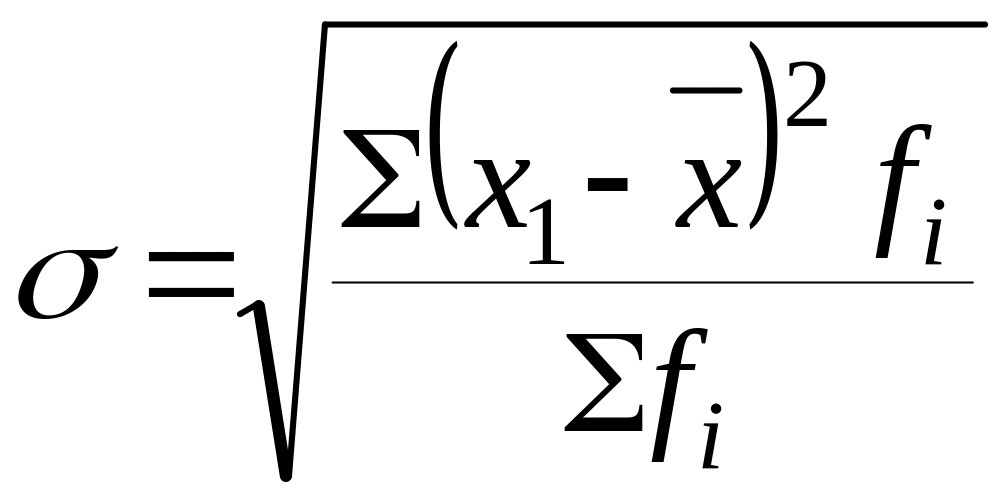(3) – среднее квадратическое отклонение взвешенное, где:

• – значения изучаемого признака (варианты);

• – объем статистической совокупности;

• – средняя арифметическая величина.

• Тема «Выборочное наблюдение» (задача № 3)

Выборочное наблюдение имеет важное значение. Это связано с сокращением и упрощением отчетности в условиях рыночной экономики.

Для вычисления средней ошибки выборки в том случае, когда генеральная совокупность представляется достаточно большой, или отношение численности выборки к численности генеральной совокупности ( ) менее 5 %, то поправкой можно пренебречь и находить ошибку выборки по способу повторного отбора, даже если сама выборка была бесповторной.

Наиболее частой ошибкой является отождествление средней ошибки, выборочной средней и средней ошибки выборочной доли. Изучая эту тему, надо хорошо усвоить, что средняя ошибка выборочной средней определяется по вариации количественного признака ( ):

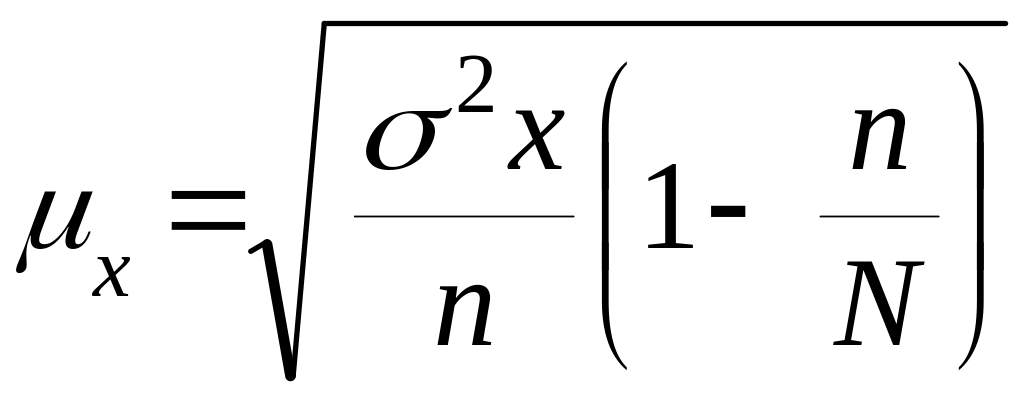(5) – (для поворотного, собственно случайного отбора).

Средняя ошибка выборочной доли (6) – (для поворотного случайного отбора) определяется по показателям дисперсии альтернативного признака , где:

• ;

• – численность единиц выборочной совокупности, обладающих исследуемым признаком.

В решении этих задач часто неверно указывается значение так называемого коэффициента доверия при заданной степени вероятности. Значение определяется по специальным таблицам, которые приведены в учебниках.

Тема «Ряды динамики» (задача № 4)

В теме излагается методология изучения развития социально-экономических явлений во времени.

Для успешного выполнения задач данной темы необходимо уяснить познавательное значение и условия применения показателей, характеризующих изменения уровней ряда динамики : абсолютный прирост , темп роста и прироста и др.

Часто допускаются ошибки при определении среднего уровня ряда динамики. Надо уяснить, что в интервальных рядах динамики (с равными интервалами) средний уровень определяется по формуле:

(8),

где: – число уровней ряда динамики.

В моментных рядах динамики (с равноотстоящими датами времени) средний уровень определяется по формуле:

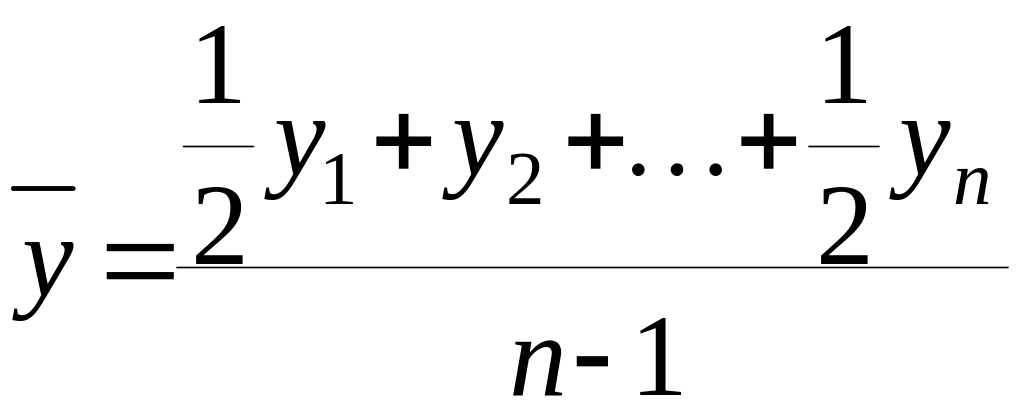(9),

где: – уровни ряда динамики соответственно на 1-ю, 2-ю, …, n-ю даты времени.

При определении среднего (среднегодового) темпа роста по абсолютным уровням ряда используется формула:

(12), где:

• – конечный уровень ряда;

• – базисный (начальный) уровень ряда;

• – средний (среднегодовой) коэффициент роста;

• – число субпериодов в изучаемом ряду динамики.

Например, если продажа товара «А» составляла в 2001 г. 353 тыс. т, а в 2007 г. – 480 тыс. т, то расчет среднегодового темпа роста производится следующим образом:

(в периоде 1998 г. ... 2004 г. – 6 лет).

Для определения среднего (среднегодового) абсолютного прироста по цепным (погодовым) приростам используется формула:

(13),

где – число цепных (погодовых) абсолютных приростов.

Средний (среднегодовой) абсолютный прирост можно определить и по абсолютным уровням ряда динамики:

(14), где:

• – конечный уровень ряда динамики;

• – базисный начальный уровень ряда динамики;

• – число субпериодов в изучаемом интервале времени.

Так, для приведенных выше данных о продаже продукта «А», среднегодовой абсолютный прирост определяется так:

тыс. тонн.

Показатели среднего темпа роста и среднего абсолютного прироста применяются при краткосрочном статистическом прогнозировании (КСП) путем экстраполяции уровня развития изучаемого явления на ближайшее будущее. При КСП предполагается, что выявленная внутри динамического ряда основная закономерность роста сохраняется и в дальнейшем развитии. Поэтому, если в статистическом ряду нет резких колебаний ценных показателей динамики, то для определения экстраполируемого уровня применяются фор мулы:

а) по среднему абсолютному приросту

(15);

б) по среднему коэффициенту роста

(16), где:

• – конечный уровень ряда динамики;

• – срок прогноза (упреждения).

Для КСП может быть использован метод экстраполяции тренда на основе аналитического выравнивания уровней ряда динамики, отображающего динамику развития явления за отдельные периоды экономического развития.

Расчет экстраполируемого уровня производится по формуле:

(17), где:

• и – параметры модели тренда;

• – показатели времени прогнозируемого периода.