- •Порядок проведення роботи
- •Обробка й аналіз результатів
- •Порядок виконання роботи
- •Обробка й аналіз результатів
- •Контрольні питання
- •Порядок виконання роботи
- •Обробка й аналіз результатів
- •Контрольні питання
- •Порядок виконання роботи
- •Обробка й аналіз результатів
- •Контрольні питання
- •5. Лабораторна робота № 5 «визначення коефіцієнтів місцевого опору»
- •Теоретичні основи роботи
- •Порядок виконання роботи
- •Обробка й аналіз результатів
- •Порядок виконання роботи
- •Обробка й аналіз результатів
- •Контрольні питання
- •7. Лабораторна робота № 7 «визначення параметрів шорсткості поверхні»
- •Теоретичні основи роботи
- •Порядок виконання роботи Обробка й аналіз результатів
- •Порядок виконання роботи
- •Виконання роботи
- •Статистична перевірка гіпотез з використанням критерію згоди пірсона
- •Виконання роботи
- •10. Додаток.
- •Десяткові кратні та частинні від одиниць si
- •11. Список літератури
Статистична перевірка гіпотез з використанням критерію згоди пірсона
У ході =100 вимірювань визначаються діаметри ( =1…100) шариків підшипника, похибка вимірювань яких розподілена за нормальним законом з параметрами і .
Визначити
значення статистики
![]() для досліджуваного параметра
(за Таблицею 9.1 визначається досліджуваний
параметр). Використовуючи критерій
згоди Пирсона, показати, наскільки
розподіл похибок площини
головного
перетину
,
осьового моменту інерції
або
,
об’єму
,
поперечного моменту інерції
,
осьового моменту опору
або
шариків підшипника можна вважати
нормальним.
для досліджуваного параметра
(за Таблицею 9.1 визначається досліджуваний
параметр). Використовуючи критерій
згоди Пирсона, показати, наскільки
розподіл похибок площини
головного
перетину
,
осьового моменту інерції
або
,
об’єму
,
поперечного моменту інерції
,
осьового моменту опору
або
шариків підшипника можна вважати
нормальним.
Виконання роботи
За допомогою датчика випадкових чисел RANDOM генерується реалізація випадкової величини ( =1…100), розподіленої рівномірно в інтервалі 0,1.
Для
нормального розподілу з нульовим
математичним очікуванням (
=0,0)
і одиничною дисперсією (
=1,0)
на основі двох послідовно узятих чисел
(
,
),
(
,
),…,(![]() ,
,![]() )
(для 100 значень мається 50 пар чисел)
одержуємо відповідно два числа (
,
),
(
,
),…,(
)
(для 100 значень мається 50 пар чисел)
одержуємо відповідно два числа (
,
),
(
,
),…,(![]() ,
,![]() )
нормально розподіленої випадкової
величини
)
нормально розподіленої випадкової
величини
, ,
( =1,3,…,99).
При одержанні реалізації нормальної випадкової величини з ненульовим математичним очікуванням і стандартним відхиленням , відмінним від одиниці, використовується наступне співвідношення
( =1…100).
Значення вибирають з Таблиці 9.2, величина =0,01 .
Для всіх значень ( =1…100) необхідно визначити реалізацію досліджуваного параметра ( =1…100) відповідно до Таблиці 9.1. Дослідження проводиться за наступною схемою:
Визначити вибіркові оцінки математичного очікування
 і дисперсії
досліджуваного параметра
і дисперсії
досліджуваного параметра
![]() ,
,
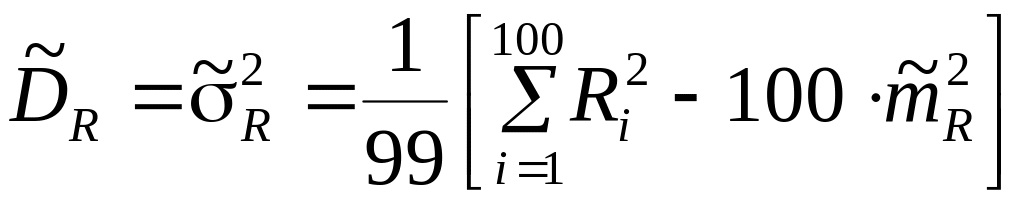 .
(9.4)
.
(9.4)
Визначити мінімальне -
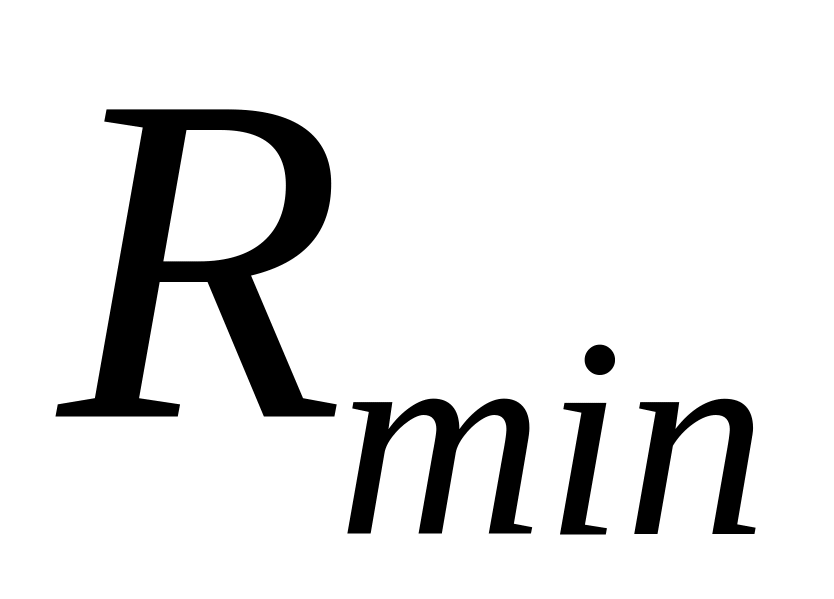 ,
максимальне -
,
максимальне -
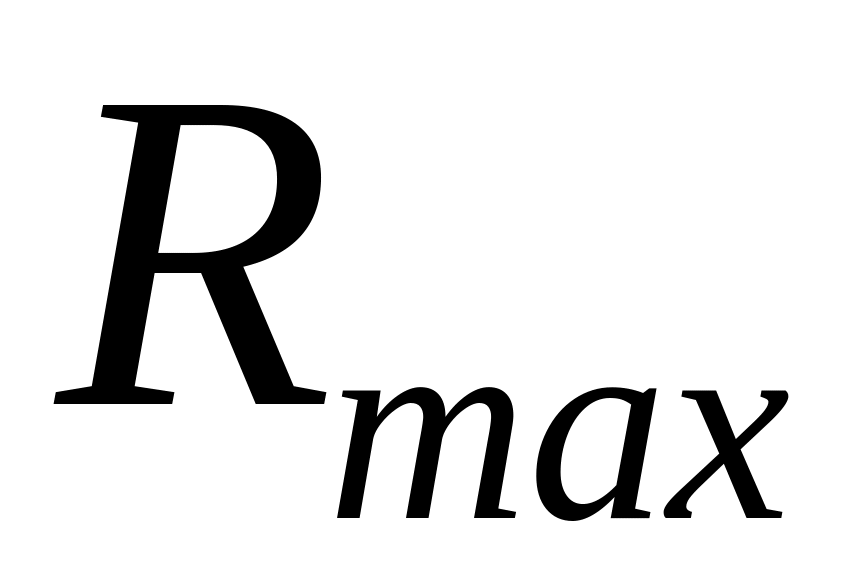 значення, розмах
значення, розмах
 .
Для нормального розподілу майже всі
значення (99,7%) випадкової величини
знаходяться в інтервалі (
.
Для нормального розподілу майже всі
значення (99,7%) випадкової величини
знаходяться в інтервалі (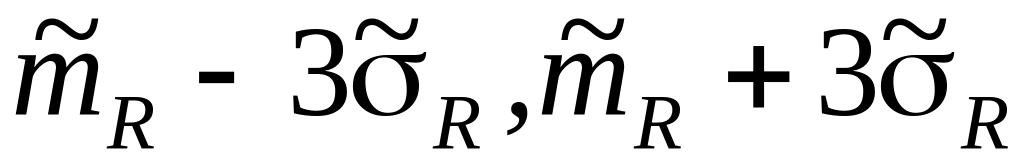 ),
величину
),
величину
 знаходять за формулою (9.4), Але є певні
рекомендації щодо побудови гістограми,
згідно з якими:
знаходять за формулою (9.4), Але є певні
рекомендації щодо побудови гістограми,
згідно з якими:
для кількості дослідів (6< ≤100) інтервал (
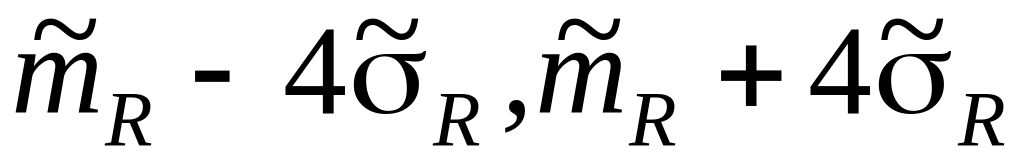 )
)для кількості дослідів (100< ≤1000) інтервал (
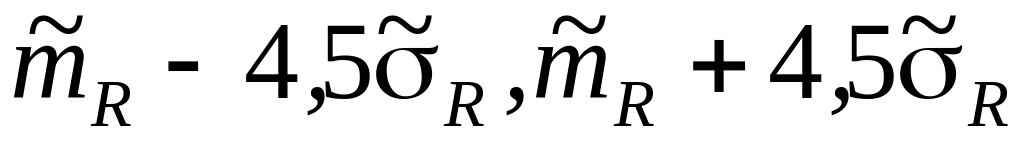 )
)для кількості дослідів (1000< ≤10000) інтервал (
 ).
).
Як
варіант через неоднозначність вибору
![]() та можливість в подальшому отримати
порожні стовпчики у побудові гістограми
можна обрати
.
та можливість в подальшому отримати
порожні стовпчики у побудові гістограми
можна обрати
.
Побудувати гістограму, згрупувавши реалізацію досліджуваного параметра ( =1…100) у
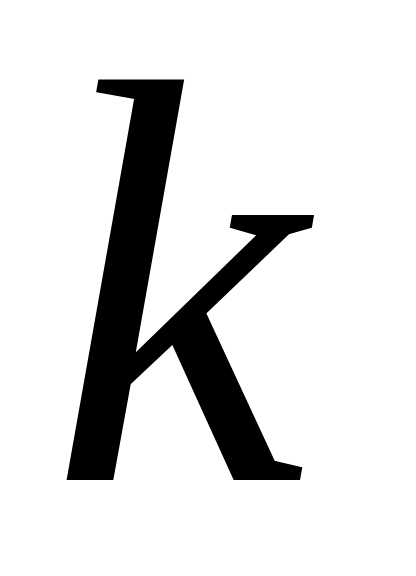 (
(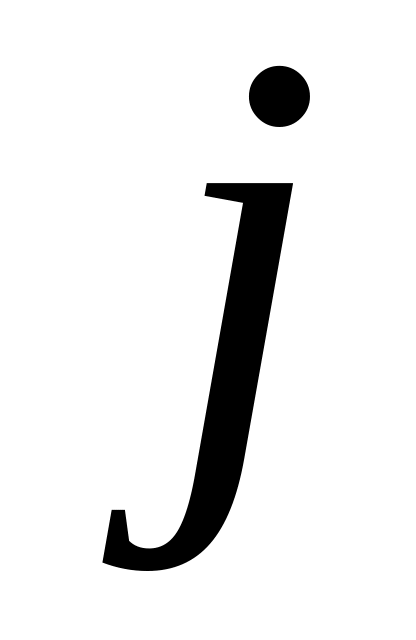 =1..
)
інтервалах (кількість інтервалів
– будь-яке ціле число від 5 до 10, в роботі
рекомендовано прийняти
=7).
Зважаючи на унімодальний характер
розподілу параметра
,
кількість інтервалів має бути непарним
числом, але це не є обов'язковим. Ширина
інтервалу
=1..
)
інтервалах (кількість інтервалів
– будь-яке ціле число від 5 до 10, в роботі
рекомендовано прийняти
=7).
Зважаючи на унімодальний характер
розподілу параметра
,
кількість інтервалів має бути непарним
числом, але це не є обов'язковим. Ширина
інтервалу
![]() .
.
Тоді границі інтервалів визначаються наступним чином:
1-й
інтервал - (![]() )
або (
)
або (![]() ),
),
2-й
інтервал - (![]() )
або (
)
або (![]() ),
),
…………………………………………………………………………………………………………
-й
інтервал - (![]() )
або (
)
або (![]() ),
),
…………………………………………………………………………………………………………
Для останнього -го інтервалу отримаємо
-й
інтервал - (![]() )
або (
)
або (![]() ),
або (
),
або (![]() ).
).
Число влучень значень параметра у кожний -й інтервал записується у вигляді масиву чисел
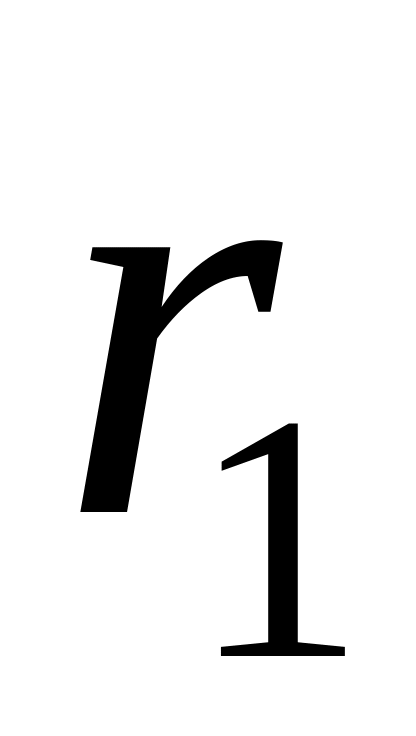 ,
,
 ,
..,
,
..,
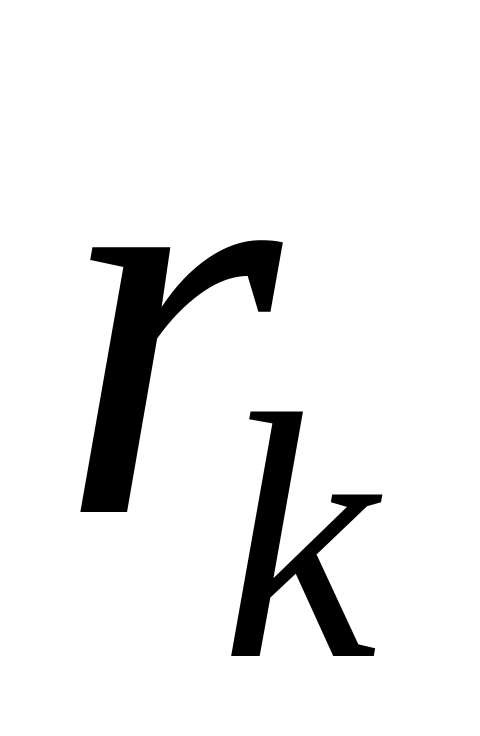 ,
причому сума
,
причому сума
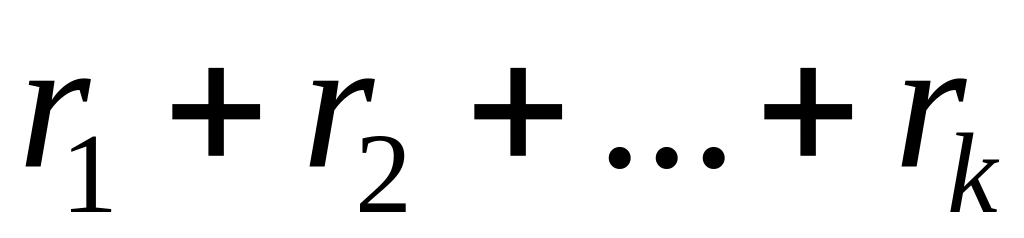 =100.
Є певні проблеми з віднесенням
значення до якогось інтервалу, коли
воно збігається з одним з граничних
значень (
=100.
Є певні проблеми з віднесенням
значення до якогось інтервалу, коли
воно збігається з одним з граничних
значень ( ),
але в даній ситуації можна рекомендувати
віднести таке проблемне значення
до ближчого до центру інтервала. Головне
уникнути подвійного додавання одного
значення до сусідніх інтервалів.
),
але в даній ситуації можна рекомендувати
віднести таке проблемне значення
до ближчого до центру інтервала. Головне
уникнути подвійного додавання одного
значення до сусідніх інтервалів.Знаючи математичне очікування і дисперсію , досліджуваний параметр підкоряють нормальному розподілові
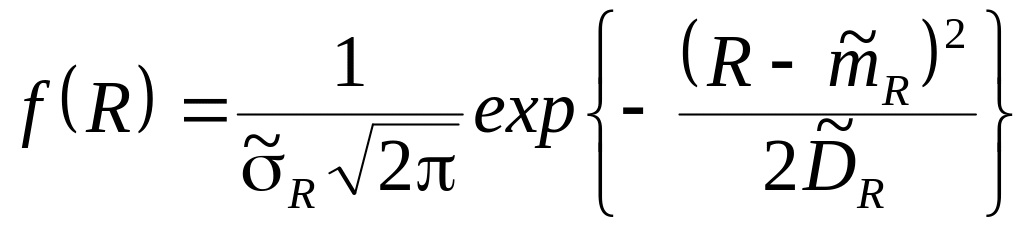 .
(9.5)
.
(9.5)
Для визначення імовірності знаходження випадкової величини, розподіленої за нормальним законом, на заданому інтервалі
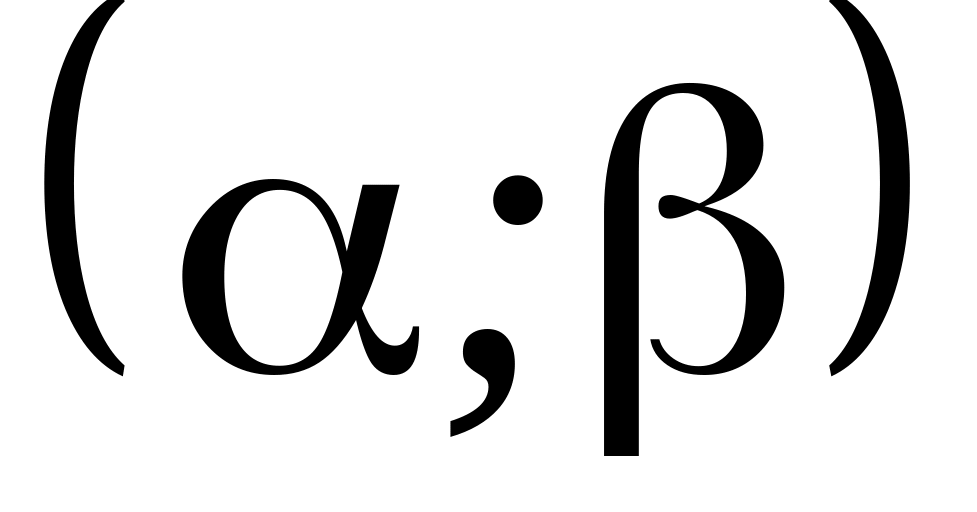 скористаємось загальними співвідношеннями
скористаємось загальними співвідношеннями
 (9.6)
(9.6)
З урахуванням функції
![]() (9.7)
(9.7)
імовірність остаточно записується у вигляді
![]() .
(9.8)
.
(9.8)
Прив’язуючись до введених позначень для границь інтервалів, для -го інтервалу запишемо
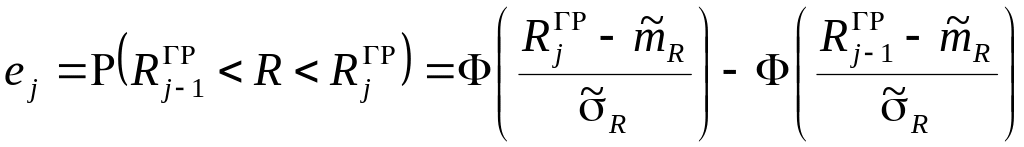 (9.9)
(9.9)
![]() .
.
Функція
![]() є непарною функцією, тобто при розрахунках
необхідно враховувати, що для від’ємного
аргументу
є непарною функцією, тобто при розрахунках
необхідно враховувати, що для від’ємного
аргументу
![]() .
Значення функції тільки для додатного
аргументу приведено в Таблиці 9.4.
.
Значення функції тільки для додатного
аргументу приведено в Таблиці 9.4.
Імовірність
знаходження випадкової величини,
розподіленої за нормальним законом),
на кожному
-му
інтервалі записується у виді масиву
чисел
![]() ,
,
![]() ,
..,
,
..,
![]() ,
причому сума
,
причому сума
![]() =1,0.
Останнє через наближене визначення за
формулою (9.9) доданків
,
,
..,
може не виконуватися та бути на рівні
0,98…0,99.
=1,0.
Останнє через наближене визначення за
формулою (9.9) доданків
,
,
..,
може не виконуватися та бути на рівні
0,98…0,99.
Визначається величина статистики
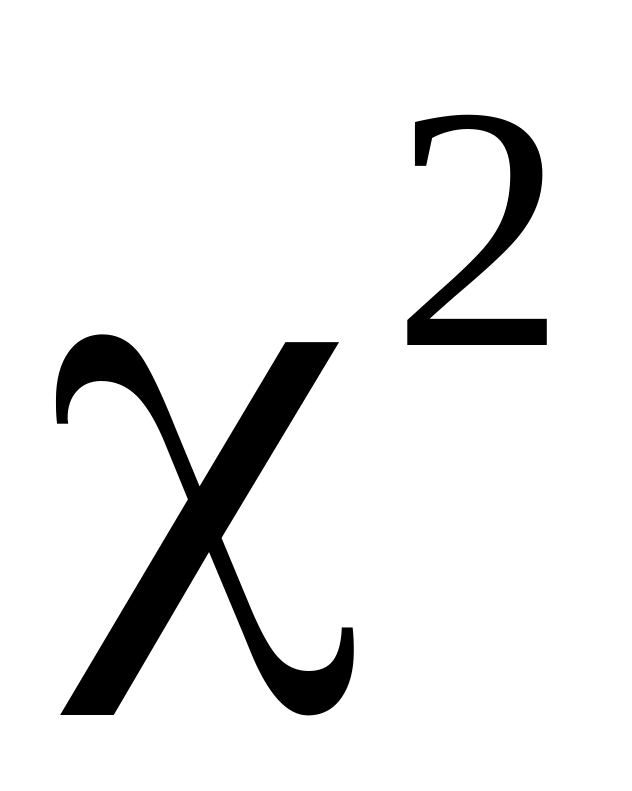 за формулою
за формулою
![]() .
(9.10)
.
(9.10)
За Таблицею 9.5 знаходимо значення
 для параметру
для параметру
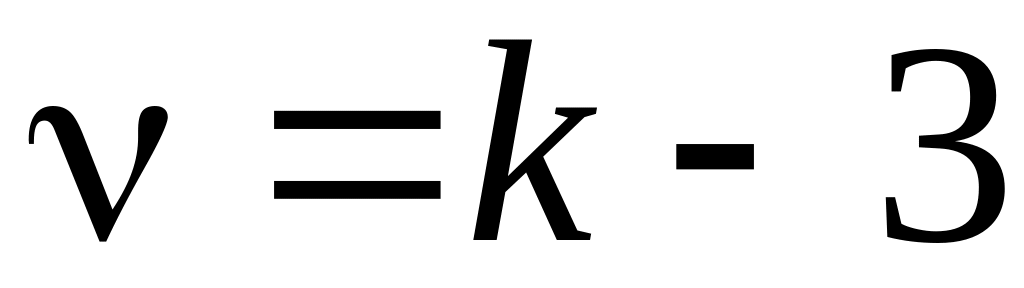 .
Імовірність «збігу» побудованої
гістограми і відповідного до неї
нормального закону визначається
величиною
-значення,
рівного
.
Імовірність «збігу» побудованої
гістограми і відповідного до неї
нормального закону визначається
величиною
-значення,
рівного
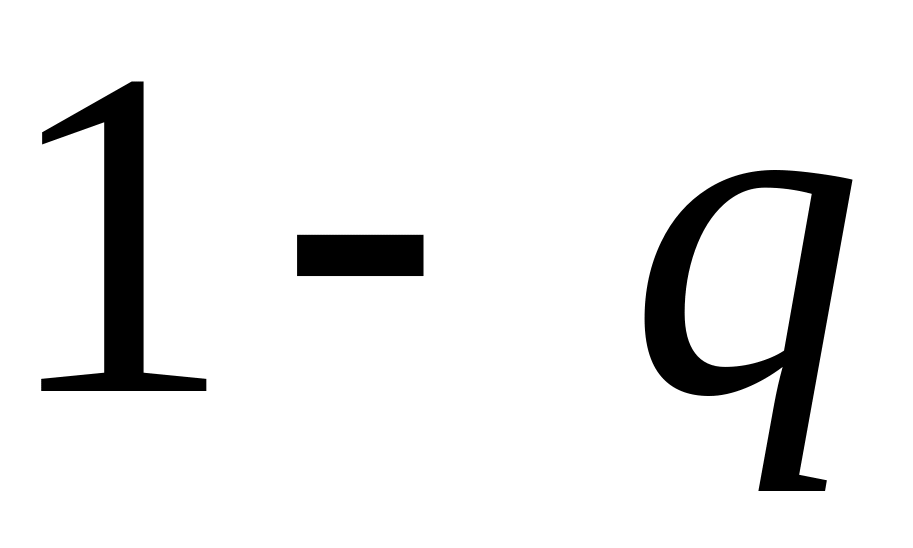 .
.
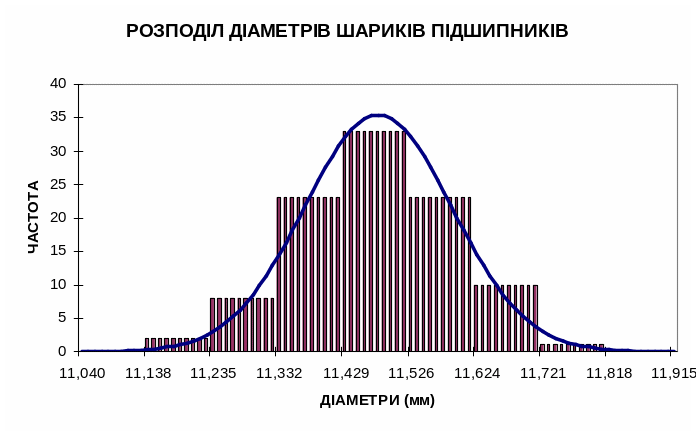
Слід зазначити, що часто при нормальному розподілі похибок прямих вимірів похибки заснованих на них непрямих вимірюваннях можуть бути розподілені за законом, відмінним від нормального. Якщо для діаметрів шариків підшипника похибки вимірювання підкоряються нормальному закону і крива розподілу симетрична щодо середнього значення діаметра, то крива розподілу похибок при обчисленні площі головного перетину, маси, моменту опору, моменту інерції і поперечного моменту інерції (тобто в тих випадках, коли в математичному вираженні величину діаметра беруть у 2-у, 3-у, 4-у ступені) у загальному випадку асиметрична. Це стає особливо помітно зі збільшенням числового інтервалу, у якому знаходяться досліджувані похибки. На рисунках представлені теоретичні криві розподілу (нормальний закон і дійсний закон, що враховує зведення величини діаметра у відповідний ступінь) для різних дисперсій значень. Видно, що в першому випадку (Рис. 9.3) обидві криві практично збігаються, а в другому (Рис. 9.5) відмінність між ними вже істотна. Тому в кожній конкретній задачі, беручи до уваги величину досліджуваних похибок і співвідносячи їх із середнім значенням досліджуваного параметра, питання нормальності розподілу вирішується дослідником.
До протоколу (стор. 62-63) виконання роботи занести такі дані:
Кількість вимірювань
Величину математичного очікування діаметрів шариків підшипників і відповідну величину середньоквадратичного відхилення
Отримані значення діаметрів шариків підшипника
Відповідні до цих діаметрів величини досліджуваного параметра
Мінімальне та максимальне значення діаметрів шариків підшипника та відповідні до них максимальне та мінімальне значення досліджуваного параметра
Послідовно: інтервал значень досліджуваного параметра, кількість значень в цьому інтервалі (емпірична, теоретична за дійсним законом розподілу, теоретична за нормальним законом розподілу)
Величини статистики для обох варіантів порівняння гістограми з теоретичним розподілом
Величина значення (беремо найближче з Таблиці 9.5) та відповідне до нього -значення, які показують ступінь збігу гістограми та розподілу.
Усі необхідні графіки мають бути побудованими.
На стор. 62-63 приведено варіант заповнення протоколу, а далі на Рис. 9.1 -9.5 показані необхідні графіки (графік на Рис. 9.1. для діаметрів не є обов'язковим). Слід зазначити, рисунки, що свідчать про некоректність приймання нормального розподілу для досліджуваного параметра (у разі =0,1 для випадку досліджень, проведених при поясненні розрахунково-графічного завдання), отримані зі суто прикладною метою - показати існуючі розбіжності між розподілами. Насправді, таких похибок при виробництві шариків підшипників не може бути ні в якому разі.
|
Рисунок 9.1. |
В
роботі у якості розмаху
прийняли інтервал (![]() ),
чим і пояснюється порожність крайніх
інтервалів.
),
чим і пояснюється порожність крайніх
інтервалів.
|
Рисунок 9.2. |
|
Рисунок 9.3. Пунктирна лінія – дійсний розподіл, суцільна – нормальний закон |
|
Рисунок 9.4. |
|
Рисунок 9.5. Пунктирна лінія – дійсний розподіл, суцільна – нормальний закон |
ПРОТОКОЛ ВИКОНАННЯ РОЗРАХУНКОВО-ГРАФІЧНОЇ РОБОТИ
(задача 2)
Кількість вимірювань |
|
100 |
Математичне очікування діаметрів шариків підшипника (мм) |
|
11.500 |
Середньоквадратичне (стандартне) відхилення (мм) |
|
0.1150 |
Діаметри шариків підшипника (мм) |
|||||||||
11.553 |
11.587 |
11.509 |
11.446 |
11.413 |
11.585 |
11.541 |
11.519 |
11.320 |
11.374 |
11.388 |
11.376 |
11.543 |
11.677 |
11.498 |
11.421 |
11.525 |
11.560 |
11.535 |
11.512 |
11.357 |
11.440 |
11.478 |
11.629 |
11.460 |
11.394 |
11.488 |
11.437 |
11.561 |
11.421 |
11.505 |
11.343 |
11.575 |
11.533 |
11.570 |
11.327 |
11.499 |
11.559 |
11.387 |
11.414 |
11.555 |
11.529 |
11.378 |
11.456 |
11.603 |
11.560 |
11.454 |
11.402 |
11.719 |
11.498 |
11.409 |
11.580 |
11.497 |
11.513 |
11.533 |
11.489 |
11.312 |
11.743 |
11.428 |
11.418 |
11.663 |
11.454 |
11.452 |
11.321 |
11.469 |
11.235 |
11.553 |
11.340 |
11.668 |
11.406 |
11.342 |
11.626 |
11.358 |
11.308 |
11.288 |
11.719 |
11.450 |
11.536 |
11.633 |
11.432 |
11.176 |
11.505 |
11.529 |
11.639 |
11.495 |
11.423 |
11.364 |
11.345 |
11.309 |
11.456 |
11.429 |
11.485 |
11.533 |
11.553 |
11.501 |
11.325 |
11.685 |
11.443 |
11.479 |
11.523 |
Величини площин головного перетину (мм2) |
|||||||||
104.824 |
105.447 |
104.039 |
102.892 |
102.298 |
105.409 |
104.615 |
104.209 |
100.639 |
101.601 |
101.859 |
101.649 |
104.649 |
107.090 |
103.836 |
102.447 |
104.313 |
104.951 |
104.500 |
104.082 |
101.308 |
102.786 |
103.472 |
106.207 |
103.156 |
101.954 |
103.659 |
102.733 |
104.967 |
102.440 |
103.958 |
101.060 |
105.235 |
104.475 |
105.144 |
100.763 |
103.847 |
104.944 |
101.846 |
102.329 |
104.857 |
104.389 |
101.683 |
103.071 |
105.731 |
104.955 |
103.036 |
102.097 |
107.854 |
103.834 |
102.226 |
105.316 |
103.810 |
104.109 |
104.465 |
103.669 |
100.501 |
108.307 |
102.571 |
102.400 |
106.838 |
103.046 |
103.001 |
100.664 |
103.306 |
99.130 |
104.830 |
100.997 |
106.921 |
102.184 |
101.039 |
106.161 |
101.323 |
100.426 |
100.068 |
107.868 |
102.970 |
104.518 |
106.279 |
102.640 |
98.106 |
103.958 |
104.392 |
106.393 |
103.771 |
102.486 |
101.433 |
101.083 |
100.451 |
103.070 |
102.598 |
103.591 |
104.473 |
104.822 |
103.895 |
100.724 |
107.243 |
102.845 |
103.494 |
104.289 |
Максимальний і мінімальний діаметри (інтервал значень) |
11.0403 |
11.915 |
|||||||
|
|
|
|
|
|
|
|
|
|
Мінімальна та максимальна площина головного перетину (інтервал значень) |
95.7308 |
111.5080 |
|||||||
Інтервали для побудови гістограми |
Частота (гістограма) |
Частота (дійсний зак.) |
Частота (нормал. зак.) |
|||||
95.731 |
- |
97.484 |
|
0 |
|
0.101 |
|
0.115 |
97.484 |
- |
99.237 |
|
2 |
|
1.408 |
|
1.460 |
99.237 |
- |
100.990 |
|
8 |
|
8.802 |
|
8.782 |
100.990 |
- |
102.743 |
|
26 |
|
25.307 |
|
25.105 |
102.743 |
- |
104.496 |
|
35 |
|
34.193 |
|
34.231 |
104.496 |
- |
106.249 |
|
20 |
|
22.100 |
|
22.289 |
106.249 |
- |
108.002 |
|
8 |
|
6.933 |
|
6.920 |
108.002 |
- |
109.755 |
|
1 |
|
1.068 |
|
1.020 |
109.755 |
- |
111.508 |
|
0 |
|
0.082 |
|
0.071 |
|
|
|
|
Σ=100 |
Σ= 99.994≈100 |
Σ= 99.993≈100 |
||
|
|
|
|
|
|
|
|
|
Величина статистики |
0.911 |
Імовірність |
≈0,99 |
|||||
Величина статистики |
0.909 |
Імовірність |
≈0,99 |
|||||
Таблиця 9.1
Номер параметру |
Параметр |
Математичний вираз для параметра |
1 |
Площина головного перетину |
|
2 |
Момент інерції (осьовий) |
|
3 |
Об’єм |
|
4 |
Поперечний (полярний) момент інерції |
|
5 |
Момент опору (осьовий) |
|
Таблиця 9.2
Номер по порядку |
Математичне очікування діаметрів (мм) |
Номер по порядку |
Математичне очікування діаметрів (мм) |
Номер по порядку |
Математичне очікування діаметрів (мм) |
1 |
1,30 |
16 |
9,12 |
31 |
20,60 |
2 |
1,59 |
17 |
9,52 |
32 |
21,40 |
3 |
2,00 |
18 |
10,32 |
33 |
22,23 |
4 |
2,38 |
19 |
11,11 |
34 |
23,02 |
5 |
3,17 |
20 |
11,50 |
35 |
23,81 |
6 |
3,50 |
21 |
12,30 |
36 |
25,40 |
7 |
3,97 |
22 |
12,70 |
37 |
27,00 |
8 |
4,176 |
23 |
13,49 |
38 |
28,58 |
9 |
5,00 |
24 |
14,30 |
39 |
30,16 |
10 |
5,16 |
25 |
15,08 |
40 |
34,92 |
11 |
5,56 |
26 |
15,88 |
41 |
36,51 |
12 |
5,95 |
27 |
16,67 |
42 |
38,10 |
13 |
6,35 |
28 |
17,46 |
43 |
41,28 |
14 |
7,14 |
29 |
19,05 |
44 |
44,45 |
15 |
8,73 |
30 |
19,84 |
45 |
50,80 |

Таблиця 9.4
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0,0 |
0,00000 |
0,00399 |
0,00798 |
0,01197 |
0,01595 |
0,01994 |
0,02392 |
0,02790 |
0,03188 |
0,03586 |
0,1 |
0,03983 |
0,04380 |
0,04776 |
0,05172 |
0,05567 |
0,05962 |
0,06356 |
0,06749 |
0,07142 |
0,07535 |
0,2 |
0,07926 |
0,08317 |
0,08706 |
0,09095 |
0,09483 |
0,09871 |
0,10257 |
0,10642 |
0,11026 |
0,11409 |
0,3 |
0,11791 |
0,12172 |
0,12552 |
0,12930 |
0,13307 |
0,13683 |
0,14058 |
0,14431 |
0,14803 |
0,15173 |
0,4 |
0,15542 |
0,15910 |
0,16276 |
0,16640 |
0,17003 |
0,17364 |
0,17724 |
0,18082 |
0,18438 |
0,18793 |
|
|
|
|
|
|
|
|
|
|
|
0,5 |
0,19146 |
0,19497 |
0,19847 |
0,20194 |
0,20540 |
0,20884 |
0,21226 |
0,21566 |
0,21904 |
0,22240 |
0,6 |
0,22574 |
0,22907 |
0,23237 |
0,23565 |
0,23891 |
0,24215 |
0,24537 |
0,24857 |
0,25174 |
0,25490 |
0,7 |
0,25803 |
0,26114 |
0,26423 |
0,26730 |
0,27035 |
0,27337 |
0,27637 |
0,27935 |
0,28230 |
0,28523 |
0,8 |
0,28814 |
0,29102 |
0,29389 |
0,29673 |
0,29954 |
0,30233 |
0,30510 |
0,30784 |
0,31056 |
0,31326 |
0,9 |
0,31593 |
0,31858 |
0,32121 |
0,32381 |
0,32638 |
0,32894 |
0,33146 |
0,33397 |
0,33645 |
0,33891 |
|
|
|
|
|
|
|
|
|
|
|
1,0 |
0,34134 |
0,34374 |
0,34613 |
0,34849 |
0,35082 |
0,35313 |
0,35542 |
0,35768 |
0,35992 |
0,36213 |
1,1 |
0,36432 |
0,36649 |
0,36863 |
0,37075 |
0,37285 |
0,37492 |
0,37696 |
0,37899 |
0,38099 |
0,38297 |
1,2 |
0,38492 |
0,38685 |
0,38876 |
0,39064 |
0,39250 |
0,39434 |
0,39615 |
0,39795 |
0,39972 |
0,40146 |
1,3 |
0,40319 |
0,40489 |
0,40657 |
0,40823 |
0,40986 |
0,41148 |
0,41307 |
0,41464 |
0,41619 |
0,41772 |
1,4 |
0,41923 |
0,42072 |
0,42218 |
0,42363 |
0,42505 |
0,42646 |
0,42784 |
0,42920 |
0,43055 |
0,43187 |
|
|
|
|
|
|
|
|
|
|
|
1,5 |
0,43318 |
0,43446 |
0,43573 |
0,43698 |
0,43821 |
0,43941 |
0,44061 |
0,44178 |
0,44293 |
0,44407 |
1,6 |
0,44519 |
0,44629 |
0,44737 |
0,44843 |
0,44948 |
0,45051 |
0,45153 |
0,45252 |
0,45351 |
0,45447 |
1,7 |
0,45542 |
0,45635 |
0,45727 |
0,45817 |
0,45906 |
0,45993 |
0,46078 |
0,46162 |
0,46245 |
0,46326 |
1,8 |
0,46405 |
0,46484 |
0,46561 |
0,46636 |
0,46710 |
0,46783 |
0,46854 |
0,46924 |
0,46993 |
0,47061 |
1,9 |
0,47127 |
0,47192 |
0,47256 |
0,47318 |
0,47380 |
0,47440 |
0,47499 |
0,47557 |
0,47613 |
0,47669 |
|
|
|
|
|
|
|
|
|
|
|
2,0 |
0,47724 |
0,47777 |
0,47829 |
0,47881 |
0,47931 |
0,47980 |
0,48029 |
0,48076 |
0,48122 |
0,48168 |
2,1 |
0,48212 |
0,48256 |
0,48298 |
0,48340 |
0,48381 |
0,48421 |
0,48460 |
0,48498 |
0,48536 |
0,48573 |
2,2 |
0,48608 |
0,48643 |
0,48678 |
0,48711 |
0,48744 |
0,48776 |
0,48808 |
0,48838 |
0,48868 |
0,48898 |
2,3 |
0,48926 |
0,48954 |
0,48982 |
0,49009 |
0,49035 |
0,49060 |
0,49085 |
0,49110 |
0,49133 |
0,49157 |
2,4 |
0,49179 |
0,49201 |
0,49223 |
0,49244 |
0,49265 |
0,49285 |
0,49304 |
0,49323 |
0,49342 |
0,49360 |
|
|
|
|
|
|
|
|
|
|
|
2,5 |
0,49378 |
0,49395 |
0,49412 |
0,49429 |
0,49445 |
0,49461 |
0,49476 |
0,49491 |
0,49505 |
0,49519 |
2,6 |
0,49533 |
0,49546 |
0,49560 |
0,49572 |
0,49585 |
0,49597 |
0,49609 |
0,49620 |
0,49631 |
0,49642 |
2,7 |
0,49653 |
0,49663 |
0,49673 |
0,49683 |
0,49692 |
0,49701 |
0,49710 |
0,49719 |
0,49728 |
0,49736 |
2,8 |
0,49744 |
0,49752 |
0,49759 |
0,49767 |
0,49774 |
0,49781 |
0,49788 |
0,49794 |
0,49801 |
0,49807 |
2,9 |
0,49813 |
0,49819 |
0,49825 |
0,49830 |
0,49835 |
0,49841 |
0,49846 |
0,49851 |
0,49855 |
0,49860 |
|
|
|
|
|
|
|
|
|
|
|
3,0 |
0,49865 |
0,49869 |
0,49873 |
0,49877 |
0,49881 |
0,49885 |
0,49889 |
0,49893 |
0,49896 |
0,49900 |
3,1 |
0,49903 |
0,49906 |
0,49909 |
0,49912 |
0,49915 |
0,49918 |
0,49921 |
0,49923 |
0,49926 |
0,49929 |
3,2 |
0,49931 |
0,49933 |
0,49936 |
0,49938 |
0,49940 |
0,49942 |
0,49944 |
0,49946 |
0,49948 |
0,49950 |
3,3 |
0,49951 |
0,49953 |
0,49955 |
0,49956 |
0,49958 |
0,49959 |
0,49961 |
0,49962 |
0,49964 |
0,49965 |
3,4 |
0,49966 |
0,49967 |
0,49969 |
0,49970 |
0,49971 |
0,49972 |
0,49973 |
0,49974 |
0,49975 |
0,49976 |
|
|
|
|
|
|
|
|
|
|
|
3,5 |
0,49977 |
0,49977 |
0,49978 |
0,49979 |
0,49980 |
0,49981 |
0,49981 |
0,49982 |
0,49983 |
0,49983 |
3,6 |
0,49984 |
0,49985 |
0,49985 |
0,49986 |
0,49986 |
0,49987 |
0,49987 |
0,49988 |
0,49988 |
0,49989 |
3,7 |
0,49989 |
0,49990 |
0,49990 |
0,49990 |
0,49991 |
0,49991 |
0,49991 |
0,49992 |
0,49992 |
0,49992 |
3,8 |
0,49993 |
0,49993 |
0,49993 |
0,49994 |
0,49994 |
0,49994 |
0,49994 |
0,49995 |
0,49995 |
0,49995 |
3,9 |
0,49995 |
0,49995 |
0,49996 |
0,49996 |
0,49996 |
0,49996 |
0,49996 |
0,49996 |
0,49997 |
0,49997 |
Значення функції
Таблиця 9.5
Процентилі розподілу 2
|
|
|||||||||||||||||
|
0,005 |
0,010 |
0,025 |
0,05 |
0,10 |
0,20 |
0,30 |
0,40 |
||||||||||
1 |
0,00004 |
0,00016 |
0,00098 |
0,00393 |
0,0158 |
0,0642 |
0,148 |
0,275 |
||||||||||
2 |
0,0100 |
0,0201 |
0,0506 |
0,103 |
0,211 |
0,446 |
0,713 |
1,02 |
||||||||||
3 |
0,0717 |
0,115 |
0,216 |
0,352 |
0,584 |
1,00 |
1,42 |
1,87 |
||||||||||
4 |
0,207 |
0,297 |
0,484 |
0,711 |
1,06 |
1,65 |
2,19 |
2,75 |
||||||||||
5 |
0,412 |
0,554 |
0,831 |
1,15 |
1,61 |
2,34 |
3,00 |
3,66 |
||||||||||
6 |
0,676 |
0,872 |
1,24 |
1,64 |
2,20 |
3,07 |
3,83 |
4,57 |
||||||||||
7 |
0,989 |
1,24 |
1,69 |
2,17 |
2,83 |
3,82 |
4,67 |
5,49 |
||||||||||
8 |
1,34 |
1,65 |
2,18 |
2,73 |
3,49 |
4,59 |
5,53 |
6,42 |
||||||||||
9 |
1,73 |
2,09 |
2,70 |
3,33 |
4,17 |
5,38 |
6,39 |
7,36 |
||||||||||
10 |
2,16 |
2,56 |
3,25 |
3,94 |
4,87 |
6,18 |
7,27 |
8,30 |
||||||||||
11 |
2,60 |
3,05 |
3,82 |
4,57 |
5,58 |
6,99 |
8,15 |
9,24 |
||||||||||
12 |
3,07 |
3,57 |
4,40 |
5,23 |
6,30 |
7,81 |
9,03 |
10,2 |
||||||||||
13 |
3,57 |
4,11 |
5,01 |
5,89 |
7,04 |
8,63 |
9,93 |
11,1 |
||||||||||
14 |
4,07 |
4,66 |
5,63 |
6,57 |
7,79 |
9,47 |
10,8 |
12,1 |
||||||||||
15 |
4,60 |
5,23 |
6,26 |
7,26 |
8,55 |
10,3 |
11,7 |
13,0 |
||||||||||
16 |
5,14 |
5,81 |
6,91 |
7,96 |
9,31 |
11,2 |
12,6 |
14,0 |
||||||||||
17 |
5,70 |
6,41 |
7,56 |
8,67 |
10,1 |
12,0 |
13,5 |
14,9 |
||||||||||
18 |
6,26 |
7,01 |
8,23 |
9,39 |
10,9 |
12,9 |
14,4 |
15,9 |
||||||||||
19 |
6,84 |
7,63 |
8,91 |
10,1 |
11,7 |
13,7 |
15,4 |
16,9 |
||||||||||
20 |
7,43 |
8,26 |
9,59 |
10,9 |
12,4 |
14,6 |
16,3 |
17,8 |
||||||||||
21 |
8,03 |
8,90 |
10,3 |
11,6 |
13,2 |
15,4 |
17,2 |
18,8 |
||||||||||
22 |
8,64 |
9,54 |
11,0 |
12,3 |
14,0 |
16,3 |
18,1 |
19,7 |
||||||||||
23 |
9,26 |
10,2 |
11,7 |
13,1 |
14,8 |
17,2 |
19,0 |
20,7 |
||||||||||
24 |
9,89 |
10,9 |
12,4 |
13,8 |
15,7 |
18,1 |
19,9 |
21,7 |
||||||||||
25 |
10,5 |
11,5 |
13,1 |
14,6 |
16,5 |
18,9 |
20,9 |
22,6 |
||||||||||
26 |
11,2 |
12,2 |
13,8 |
15,4 |
17,3 |
19,8 |
21,8 |
23,6 |
||||||||||
27 |
11,8 |
12,9 |
14,6 |
16,2 |
18,1 |
20,7 |
22,7 |
24,5 |
||||||||||
28 |
12,5 |
13,6 |
15,3 |
16,9 |
18,9 |
21,6 |
23,6 |
25,5 |
||||||||||
29 |
13,1 |
14,3 |
16,0 |
17,7 |
19,8 |
22,5 |
24,6 |
26,5 |
||||||||||
30 |
13,8 |
15,0 |
16,8 |
18,5 |
20,6 |
23,4 |
25,5 |
27,4 |
||||||||||
35 |
17,2 |
18,5 |
20,6 |
22,5 |
24,8 |
27,8 |
30,2 |
32,3 |
||||||||||
40 |
20,7 |
22,2 |
24,4 |
26,5 |
29,1 |
32,3 |
34,9 |
37,1 |
||||||||||
45 |
24,3 |
25,9 |
28,4 |
30,6 |
33,4 |
36,9 |
39,6 |
42,0 |
||||||||||
50 |
28,0 |
29,7 |
32,4 |
34,8 |
37,7 |
41,4 |
44,3 |
46,9 |
||||||||||
|
|
|||||||||||||||||
|
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
0,95 |
0,975 |
0,990 |
0,995 |
0,999 |
||||||||
1 |
0,46 |
0,71 |
1,07 |
1,64 |
2,71 |
3,84 |
5,02 |
6,63 |
7,88 |
10,8 |
||||||||
2 |
1,39 |
1,83 |
2,41 |
3,22 |
4,61 |
5,99 |
7,38 |
9,21 |
10,6 |
13,8 |
||||||||
3 |
2,37 |
2,95 |
3,67 |
4,64 |
6,25 |
7,81 |
9,35 |
11,3 |
12,8 |
16,3 |
||||||||
4 |
3,36 |
4,04 |
4,88 |
5,99 |
7,78 |
9,49 |
11,1 |
13,3 |
14,9 |
18,5 |
||||||||
5 |
4,35 |
5,13 |
6,06 |
7,29 |
9,24 |
11,1 |
12,8 |
15,1 |
16,7 |
20,5 |
||||||||
6 |
5,35 |
6,21 |
7,23 |
8,56 |
10,6 |
12,6 |
14,4 |
16,8 |
18,5 |
22,5 |
||||||||
7 |
6,35 |
7,28 |
8,38 |
9,80 |
12,0 |
14,1 |
16,0 |
18,5 |
20,3 |
24,3 |
||||||||
8 |
7,34 |
8,35 |
9,52 |
11,0 |
13,4 |
15,5 |
17,5 |
20,1 |
22,0 |
26,1 |
||||||||
9 |
8,34 |
9,41 |
10,7 |
12,2 |
14,7 |
16,9 |
19,0 |
21,7 |
23,6 |
27,9 |
||||||||
10 |
9,34 |
10,5 |
11,8 |
13,4 |
16,0 |
18,3 |
20,5 |
23,2 |
25,2 |
29,6 |
||||||||
11 |
10,3 |
11,5 |
12,9 |
14,6 |
17,3 |
19,7 |
21,9 |
24,7 |
26,8 |
31,3 |
||||||||
12 |
11,3 |
12,6 |
14,0 |
15,8 |
18,5 |
21,0 |
23,3 |
26,2 |
28,3 |
32,9 |
||||||||
13 |
12,3 |
13,6 |
15,1 |
17,0 |
19,8 |
22,4 |
24,7 |
27,7 |
29,8 |
34,5 |
||||||||
14 |
13,3 |
14,7 |
16,2 |
18,2 |
21,1 |
23,7 |
26,1 |
29,1 |
31,3 |
26,1 |
||||||||
15 |
14,3 |
15,7 |
17,3 |
19,3 |
22,3 |
25,0 |
27,5 |
30,6 |
32,8 |
37,7 |
||||||||
16 |
15,3 |
16,8 |
18,4 |
20,5 |
23,5 |
26,3 |
28,8 |
32,0 |
34,3 |
39,3 |
||||||||
17 |
16,3 |
17,8 |
19,5 |
21,6 |
24,8 |
27,6 |
30,2 |
33,4 |
35,7 |
40,8 |
||||||||
18 |
17,3 |
18,9 |
20,6 |
22,8 |
26,0 |
28,9 |
31,5 |
34,8 |
37,2 |
42,3 |
||||||||
19 |
18,3 |
19,9 |
21,7 |
23,9 |
27,2 |
30,1 |
32,9 |
36,2 |
38,6 |
43,8 |
||||||||
20 |
19,3 |
21,0 |
22,8 |
25,0 |
28,4 |
31,4 |
34,2 |
37,6 |
40,0 |
45,3 |
||||||||
21 |
20,3 |
22,0 |
23,9 |
26,9 |
29,6 |
32,7 |
35,5 |
38,9 |
41,4 |
46,8 |
||||||||
22 |
21,3 |
23,0 |
24,9 |
27,3 |
30,8 |
33,9 |
36,8 |
40,3 |
42,8 |
48,3 |
||||||||
23 |
22,3 |
24,1 |
26,0 |
28,4 |
32,0 |
35,2 |
38,1 |
41,6 |
44,2 |
49,7 |
||||||||
24 |
23,3 |
25,1 |
27,1 |
29,6 |
33,2 |
36,4 |
39,4 |
43,0 |
45,6 |
51,2 |
||||||||
25 |
24,3 |
26,1 |
28,2 |
30,7 |
34,4 |
37,7 |
40,6 |
44,3 |
46,9 |
52,6 |
||||||||
26 |
25,3 |
27,2 |
29,2 |
31,8 |
35,6 |
38,9 |
41,9 |
45,6 |
48,3 |
54,1 |
||||||||
27 |
26,3 |
28,2 |
30,3 |
32,9 |
36,7 |
40,1 |
43,2 |
47,0 |
49,6 |
55,5 |
||||||||
28 |
27,3 |
29,2 |
31,4 |
34,0 |
37,9 |
41,3 |
44,5 |
48,3 |
51,0 |
56,9 |
||||||||
29 |
28,3 |
30,3 |
32,5 |
35,1 |
39,1 |
42,6 |
45,7 |
49,6 |
52,3 |
58,3 |
||||||||
30 |
29,3 |
31,3 |
33,5 |
36,3 |
40,3 |
43,8 |
47,0 |
50,9 |
53,7 |
59,7 |
||||||||
35 |
34,3 |
36,5 |
38,9 |
41,8 |
46,1 |
49,8 |
53,2 |
57,3 |
60,3 |
66,6 |
||||||||
40 |
39,3 |
41,6 |
44,2 |
47,3 |
51,8 |
55,8 |
59,3 |
63,7 |
66,8 |
73,4 |
||||||||
45 |
44,3 |
46,8 |
49,5 |
52,7 |
57,5 |
61,7 |
65,4 |
70,0 |
73,2 |
80,1 |
||||||||
50 |
49,3 |
51,9 |
54,7 |
58,2 |
63,2 |
67,5 |
71,4 |
76,2 |
79,5 |
86,7 |
||||||||