3.5. Истечение жидкости через отверстия и насадки
3.5.1. Истечение через отверстие в тонкой стенке.
Рассмотрим истечение жидкости из бака через малое отверстие в тонкой стенке (рис.3.7). Отверстие считается малым, если его вертикальный размер значительно меньше глубины погружения h под свободную поверхность и стенки резервуара не оказывают влияния на структуру истекающей струи. Отверстие диаметром d будет малым, если с > 3d и h > 3d. Стенка считается тонкой, если вытекающая струя соприкасается только с кромкой отверстия, не касаясь боковой поверхности, т.е. если ее толщина δ < 0,2d. К отверстию жидкость притекает со всех сторон. Вблизи отверстия линии тока жидкости криволинейны. В связи с этим площадь поперечного сечения струи на расстоянии (0,5...1)d от отверстия, где линии тока становятся параллельными, меньше площади отверстия. Происходит сжатие струи. Сжатие струи называется совершенным, если на него не оказывает влияние близость стенок бака. Таким образом, истечение жидкости через малое отверстие будет совершенным. Обозначим площадь сжатого сечения струи Sc, а площадь отверстия - S. Тогда Sс = εS, где ε - коэффициент сжатия струи, равный отношению площадей сжатого сечения и отверстия. Величина ε зависит от формы отверстия, от положения отверстия относительно стенок бака и от числа Рейнольдса.
Определим скорость истечения жидкости из отверстия и ее расход.
1. Ввиду простоты системы (бак - отверстие) делить ее на отдельные участки нет смысла.
2. Скорость истечения определим в сжатом сечении струи, поскольку в этом сечении линии тока параллельны, а профиль скорости близок к однородному. В сжатом сечении расположим сечение 2-2 расчетного участка. Сечение 1-1 расположим на свободной поверхности жидкости в баке. Плоскость сравнения 0 - 0 пусть совпадает с осью отверстия.
3. Запишем условия на границах выделенного участка: z1 = h - глубина погружения отверстия под свободную поверхность; р1 = р0 - давление на свободной поверхности; u1 = 0; z2=0; p2 = рH - давлению атмосферы, в которую истекает струя (оно постоянно по сечению струи, так как линии тока в сжатом сечении параллельны оси отверстия); u2 = и - искомой скорость истечения жидкости из отверстия.
4. Запишем уравнение Бернулли в общем виде:
.
Это уравнение конкретизируем в соответствии с условиями на границах участка, т.е. подставим в него граничные условия:
.
Потери полного давления при истечении выражены в виде местных потерь согласно формуле Вейсбаха. Последнее выражение позволяет определить скорость истечения в виде, полагая поток жидкости в сжатом сечении турбулентным (α = 1):
Величина
называется коэффициентом скорости.
Таким образом:
где Δр=р0−рн - перепад давления на отверстии.
В случае, когда Δр » ρgh, скорость истечения вычисляем так:
Если давление в баке и атмосфере одинаковы, то скорость истечения будет равна:
.
Коэффициент скорости учитывает влияние вязкости на величину скорости истечения. Если жидкость идеальная (невязкая), то ζ, = 0 и α = 1, так как в сжатом сечении неравномерность распределения кинетической энергии вызывается только вязким взаимодействием истекающей струи с окружающей средой. Поэтому скорость истечения идеальной жидкости вычисляется по формулам:
; 
; 
,
а коэффициент скорости можно записать как отношение скоростей истечения вязкой и идеальной жидкостей:
φ = и/иид.
Объемный расход жидкости в сжатом сечении:
Q=uSc,
а при использовании коэффициентов сжатия струи ε и скорости φ
Q = εφuидSс.
Произведение μ=εφ называют коэффициентом расхода. Он показывает, во сколько раз расход вязкой жидкости Q отличается от расхода идеальной (невязкой) жидкости Qид с равномерным профилем скорости в отверстии:
μ. = Q/Qид.
Как и коэффициент сжатия струи, значения коэффициентов скорости и расхода зависят от формы отверстия и от числа Рейнольдса. Очевидно, что они всегда меньше единицы.
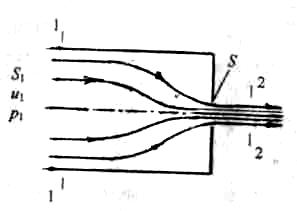
При несовершенном сжатии на истечение жидкости оказывают влияние боковые стенки резервуара, которые частично направляют жидкость к отверстию. В результате струя при выходе из отверстия сжимается в меньшей степени (рис.3.8). При истечении маловязких жидкостей из резервуара через круглое отверстие в торцевой стенке коэффициент сжатия εн можно вычислять по эмпирической формуле:
εн=ε +0,37n2,
в которой п = S/S1 - отношение площадей отверстия и поперечного сечения резервуара.
Коэффициенты сопротивления ζ и скорости φ полагают независимыми от отношения площадей п.
Рис.3.8 |
Запишем уравнение расхода и уравнение Бернулли для участка потока, ограниченного сечениями 1-1 и 2-2 (рис.3.8) для определения скорости истечения при несовершенном сжатии: u1S1 = u2S2;
|
.
На границах участка:
z1=z2=0; u2 = и- искомая скорость истечения; S2 = εн S - площадь сжатого сечения струи; S - площадь отверстия.
Из уравнения расхода следует, что u1 = εн п·и, а из уравнения Бернулли:
.
При истечении с большими числами Рейнольдса, когда движение жидкости турбулентное, полагают α2 = 1, ζ = 0,065 и скорость жидкости и расход при несовершенном сжатии можно вычислять тогда по формулам:
;
.