3.2. Простой трубопровод

Простым трубопроводом называется трубопровод постоянного сечения, без разветвлений, содержащий в общем случае несколько местных сопротивлений (рис.3.1).

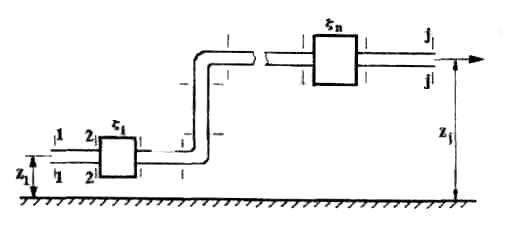
Рис.3.1

Уравнение Бернулли для участка 1 - j может быть записано в таком виде

(3.1)

или

, (3.1а)

где - суммарный коэффициент сопротивления трубопровода.

Если величину р₁/ρg - необходимо определить, то ее называют потребным напором и обозначают Н_потр. Если эта величина задана, то ее называют располагаемым напором и обозначают Н_расп. Из формулы для потребного (располагаемого) напора видно, потребный напор должен затратиться на преодоление гидравлических сопротивлений, на подъем жидкости и на обеспечения необходимого давления p_j.

Запишем выражение для потребного напора в таком простом виде:

(3.2)

В этой формуле называется статической частью потребного (располагаемого) напора, а - сумме потерь напора на расчетном участке простого трубопровода.

Для ламинарного режима будем иметь

(3.3)

где

; m = 1. (3.4)

Для турбулентного режима течения будем иметь:

(3.5)

где

а m = 2 (3.6).

Величина К в формуле (3.2) называется удельным сопротивлением трубопровода. Формулы (3.1)...(3.6) являются основой для расчета простых трубопроводов. По этим формулам можно построить кривую потребного напора, т.е. зависимость потребного напора от расхода жидкости H_потр=H(Q). Можно пользоваться вместо кривой потребного напора и характеристикой трубопровода - зависимостью потерь напора от расхода:

.

При расчете простого трубопровода можно сформулировать три постановки задачи

Задача 1

Задаются расход жидкости Q ее свойства ρ, μ, размеры трубопровода d, l и его шероховатость Δ, виды и количество местных сопротивлений n и нивелирные высоты z_j,, z₁. Требуется определить потребный напор

Решение

1. Вычисляется среднерасходная скорость и число Рейнольдса:

u=Q/S; Re=u·d/ν.

2. С помощью справочников определяются коэффициенты путевых и местных потерь напора.

3. Определяется потребный напор .

Задача 2

Задаются: свойства жидкости ρ, μ, размеры трубопровода l, d, шероховатость, виды и количество местных сопротивлений, располагаемый напор Н_расп. Требуется определить расход жидкости Q.

Решение

Так как число Рейнольдса в данной задаче определить нельзя, то по формулам (3.2) и (3.3) выражаем расход через критическое число Рейнольдса Re_кр=2300. Затем вычисляем критический напор Н_кр. Сравнив критический напор с располагаемым, определим режим течения. При ламинарном течении задача решается с помощью формул (3.2) и (3.3). При турбулентном режиме течения задача может быть решена графоаналитическим методом:

1. задается ряд значений расхода;.

2. для каждого значения расхода определяются число Рейнольдса, коэффициенты путевых и местных потерь напора, потребный напор;

3. строится кривая потребного напора Н_потр=Н(Q);

4. по заданному напору Н_расп находится искомый расход Q.

Задачу также можно решить методом дихотомии или методом простых итераций.

Для этого в первом приближении следует задаться коэффициентом путевых потерь λ=0,03 или, если задана шероховатость Δ, определить ее из (10) при Re→∞.

Задача 3

Задаются: расход жидкости и ее свойства, виды и количества местных сопротивлений, длина трубопровода и шероховатость омываемой поверхности, располагаемый напор. Требуется определить диаметр трубопровода.

Решение

Выражаем расход и скорость через критическое число Рейнольдса Re_кр=2300 и по формулам (3.2) и (3.3) вычисляем критический напор Н_кр. Сравнив Н_кр с Н_расп, однозначно определяем режим течения. При ламинарном режиме течения задача решается просто с использованием формул (3.2) и (3.3). При турбулентном режиме задача решается графически.

Графоаналитический метод решения выглядит следующим образом.

1. Задается ряд значений диаметров d.

2. Для каждого значения d определяются скорость жидкости, число Рейнольдса, коэффициенты путевых и местных потерь напора и потребный напор.

3. Строится график зависимости Н_потр = Н(d).

4. По заданному значению располагаемого напора определяется диаметр трубопровода, а по нему выбирается ближайший к стандартному

5. Уточняется значение расхода при заданном значении располагаемого напора или величина располагаемого напора при заданном расходе для выбранного стандартного диаметра трубопровода.